樹遍歷
一棵 樹 是圖的一種特殊情況，因此上一章的 圖遍歷 演算法也適用於樹。圖遍歷可以從任何節點開始，但在樹的情況下，遍歷總是從根節點開始。二叉樹可以以三種額外的遍歷方式進行遍歷。以下樹將作為重複出現的示例。
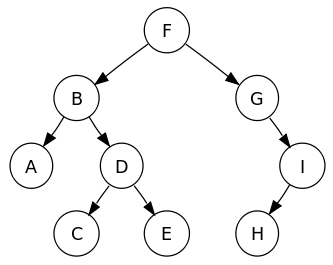
以廣度優先順序遍歷樹意味著，在訪問節點 X 之後，將訪問 X 的所有子節點，然後訪問 X 的所有“孫子節點”（即子節點的子節點），然後訪問 X 的所有“曾孫子節點”，等等。換句話說，樹是透過掃描一層中的寬度來遍歷的，然後再訪問下一層，如動畫所示
節點的子節點可以以任何順序訪問，但請記住演算法使用佇列，因此如果節點 X 在節點 Y 之前入隊（在動畫中為灰色），則 X 的子節點將在 Y 的子節點之前被訪問（在動畫中為黑色）。對於本章開頭的示例樹，兩種可能的廣度優先遍歷是 F B G A D I C E H 和 F G B I D A H E C。在第二次遍歷中，G 在 B 之前被訪問，所以 I 在 A 和 D 之前被訪問。
|
練習：廣度優先遍歷 列出相同樹的另外兩個可能的廣度優先遍歷。 答案 由於 F、B 和 D 每個都有兩個子節點，因此總共有 2*2*2=8 種可能的廣度優先遍歷
第一個和最後一個遍歷已經在上面給出，因此您可以列出任何其他兩個。 |
顧名思義，深度優先遍歷將盡可能地沿著樹的一條分支向下遍歷，即直到它在葉子上停止，然後再嘗試其他分支。從同一個父節點開始的各種分支可以以任何順序探索。對於示例樹，兩種可能的深度優先遍歷是 F B A D C E G I H 和 F G I H B D E C A。
|
練習：廣度優先遍歷 列出相同樹的另外兩個可能的深度優先遍歷。 答案 由於 F、B 和 D 每個都有兩個子節點，因此總共有 2*2*2=8 種可能的深度優先遍歷
第一個和最後一個遍歷已經在上面給出，因此您可以列出任何其他兩個。 |
|
練習：深度和廣度優先遍歷 列出此樹的 一個 廣度優先遍歷和 一個 深度優先遍歷： 答案 可能的深度優先遍歷是
可能的廣度優先遍歷是
|
- 深度優先遍歷通常使用堆疊
- 廣度優先遍歷通常使用佇列
二叉樹通常從左到右遍歷，但從右到左的遍歷也是可能的，並且可能會出現在考試問題中。因此，在本節的其餘部分，我們將始終明確說明方向。
如果每個節點都在訪問其兩個子樹 之前 被訪問，則稱為 先序 遍歷。從左到右的先序遍歷的演算法是
- 訪問根節點（通常輸出它）
- 對左子樹進行先序遍歷
- 對右子樹進行先序遍歷
可以使用以下方法實現，使用前一個單元中定義的 樹資料結構
sub PreOrder(TreeNode)
Output(TreeNode.value)
If LeftPointer(TreeNode) != NULL Then
PreOrder(TreeNode.LeftNode)
If RightPointer(TreeNode) != NULL Then
PreOrder(TreeNode.RightNode)
end sub
由於演算法完全確定了訪問節點的順序，因此對於每個二叉樹，只有一個可能的從左到右的先序遍歷。對於我們的示例樹，它是一個二叉樹，它是 F B A D C E G I H。
由於先序遍歷總是沿著一個分支（左或右）向下遍歷，然後再移動到另一個分支，因此先序遍歷始終是可能的深度優先遍歷之一。
如果每個節點都在訪問其子樹 之後 被訪問，則稱為 後序 遍歷。從左到右的後序遍歷的演算法是
- 對左子樹進行後序遍歷
- 對右子樹進行後序遍歷
- 訪問根節點（通常輸出它）
可以使用以下方法實現
sub PostOrder(TreeNode)
If LeftPointer(TreeNode) != NULL Then
PostOrder(TreeNode.LeftNode)
If RightPointer(TreeNode) != NULL Then
PostOrder(TreeNode.RightNode)
Output(TreeNode.value)
end sub
對於每個二叉樹，只有一個從左到右的後序遍歷。對於我們的示例樹，它是 A C E D B H I G F。
如果每個節點都在訪問其左子樹和右子樹 之間 被訪問，則稱為 中序 遍歷。從左到右的中序遍歷的演算法是
- 對左子樹進行中序遍歷
- 訪問根節點（通常輸出它）
- 對右子樹進行中序遍歷
可以使用以下方法實現
sub InOrder(TreeNode)
If LeftPointer(TreeNode) != NULL Then
InOrder(TreeNode.LeftNode)
Output(TreeNode.value)
If RightPointer(TreeNode) != NULL Then
InOrder(TreeNode.RightNode)
end sub
對於每個二叉樹，只有一個從左到右的中序遍歷。對於我們的示例樹，它是 A B C D E F G H I。請注意，節點是以升序訪問的。這不是巧合。
在像我們的示例樹這樣的二叉搜尋樹中，左子樹中的值小於根，右子樹中的值大於根，因此從左到右的中序遍歷將以升序訪問節點。
|
練習：中序遍歷 語句“中序遍歷總是以升序訪問節點”是真還是假？ 答案 它是錯誤的。中序遍歷只有在它是從左到右的遍歷 並且 樹是二叉搜尋樹時，才會以升序訪問節點。 如何更改上面的演算法以按降序訪問二叉搜尋樹的節點？ 答案 從右到左的中序遍歷將產生所需的順序
|
在考試中，你可能會被給出一些遍歷虛擬碼和一棵二叉樹，並被要求按照程式碼訪問節點的順序列出節點。
首先要仔細檢視程式碼並檢查
- 節點是在訪問子樹之前（先序）、之間（中序）還是之後（後序）訪問的？
- 左子樹是在右子樹之前訪問還是反過來？
例如，以下程式碼執行從左到右的遍歷，註釋顯示了根節點的訪問位置可能在哪裡。
sub Traversal(TreeNode)
'Output(TreeNode.value) REM Pre-Order
If LeftPointer(TreeNode) != NULL Then
Traversal(TreeNode.LeftNode)
'Output(TreeNode.value) REM In-Order
If RightPointer(TreeNode) != NULL Then
Traversal(TreeNode.RightNode)
'Output(TreeNode.value) REM Post-Order
end sub
假設它是從左到右的遍歷。一旦你知道從節點訪問的位置，是先序、中序還是後序遍歷，你就可以按照如下方式標註二叉樹的每個節點：
| 遍歷型別 | 輸出程式碼位置 | 放置標記的位置 |
|---|---|---|
| 先序 | 頂部 | 左側 |
| 中序 | 中間 | 底部 |
| 後序 | 底部 | 右側 |
最後，圍繞樹逆時針畫一條線，連線這些標記。沿著這條線，在遇到標記時寫下每個節點：這將是程式碼訪問節點的順序。以下是三種可能的從左到右遍歷。
- 三種不同型別的從左到右遍歷
-
先序遍歷
FBADCEGIH -
中序遍歷
ABCDEFGHI -
後序遍歷
ACEDBHIGF
如你所見，遵循這個技巧，你將得到與上面部分相同的答案。
如果遍歷是從右到左，你必須畫一條順時針線，並交換先序或後序標記的位置。
| 遍歷型別 | 輸出程式碼位置 | 從左到右遍歷的標記 | 從右到左遍歷的標記 |
|---|---|---|---|
| 先序 | 頂部 | 左側 | 右側 |
| 中序 | 中間 | 底部 | 底部 |
| 後序 | 底部 | 右側 | 左側 |
如果樹是二叉搜尋樹，並且要求你進行中序遍歷，你應該按照升序（對於從左到右的遍歷）或降序（對於從右到左的遍歷）訪問節點。如果它不是二叉搜尋樹，中序遍歷不會按照升序或降序訪問節點，但先序或後序遍歷可能會，這將取決於節點在樹中的位置。
雖然在本節中，為了清晰起見，我們始終明確地說明是左到右還是右到左遍歷，但先序、中序和後序術語的典型用法隱含著左到右遍歷，除非有相反的說明。
|
練習：二叉樹遍歷 對於以下二叉樹，執行先序、中序和後序遍歷。 答案 如果沒有其他說明，則假定從左到右遍歷。
以下程式碼描述了哪種遍歷 sub Traverse(TreeNode)
If LeftPointer(TreeNode) != NULL Then
Traverse(TreeNode.LeftNode)
Output(TreeNode.value)
If RightPointer(TreeNode) != NULL Then
Traverse(TreeNode.RightNode)
end sub
答案 中序遍歷，因為節點訪問位於程式碼的中心，並且左子樹在右子樹之前遍歷。 以下程式碼的作用是什麼？ sub P(TreeNode)
If RightPointer(TreeNode) != NULL Then
P(TreeNode.RightNode)
If LeftPointer(TreeNode) != NULL Then
P(TreeNode.LeftNode)
Output(TreeNode.value)
end sub
答案 它執行從右到左的後序遍歷，因為它首先訪問右子樹，然後訪問左子樹，最後訪問節點。 使用以下二叉樹
答案
|
.svg)