程式設計概念：圖

圖 - 用於模擬某個集合中物件之間關係的圖表，由邊（線）和頂點（點）組成

當兩個頂點由一條邊連線時，這兩個頂點被稱為鄰居。頂點的度是指它連線到的其他頂點的數量（或它擁有的鄰居數量）。圖用於記錄事物之間的關係。圖的常見用途包括地圖、社交網路、化學化合物和電路。我們將重點關注地圖，其中圖將用於模擬一些東英格蘭城鎮，並找到兩個地點之間的最短距離，例如您手機上的方向查詢GPS應用程式。下面是一個無向圖（沒有箭頭），顯示了東英格蘭城鎮的簡化地圖

東英格蘭城鎮之間的道路

在上圖中，我們有 7 個頂點和 11 條邊。Dunwich 與 Blaxhall 和 Harwich 相鄰。Clacton 有 3 條邊直接連線到 3 個其他頂點，因此它的度為 3。

練習：圖 列出 Tiptree 的所有鄰居 答案 Feering Maldon Clacton Harwich Tiptree 的度是多少 答案 4 Dunwich 的度是多少 答案 2 以下圖有多少條邊和頂點 答案 邊 = 5 頂點 = 6

帶標籤或加權圖

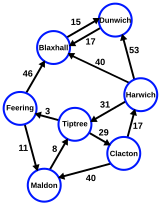
帶標籤的圖與上圖幾乎相同，但邊上附加了一些內容（通常是數值）。這在對映應用程式中很有用，當您想要找到頂點之間的最短距離或時間時。

東英格蘭城鎮之間的加權道路

練習：帶標籤或加權圖 Harwich 和 Feering 之間的最短距離是多少？ 答案 Harwich 到 Tiptree = 31 Tiptree 到 Feering = 3 總計 = 34 Blaxhall 和 Clacton 之間的最短距離是多少？ 答案 Blaxhall 到 Harwich = 40 Harwich 到 Clacton = 17 總計 = 57 Maldon 和 Dunwich 之間的最短距離是多少？ 答案 Maldon 到 Feering = 11 Feering 到 Blaxhall = 46 Blaxhall 到 Dunwich = 15 總計 = 72 您可能還有 Maldon 到 Tiptree = 8 Tiptree 到 Feering = 3 Feering 到 Blaxhall = 46 Blaxhall 到 Dunwich = 15 總計 = 72 選擇最佳路線是一項非常複雜的任務

有向圖

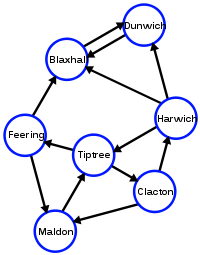
一個有向圖的例子

有向圖與普通圖非常相似，但不出所料，它們具有方向。您應該將它們視為城鎮或城市中的道路系統。一些道路將是單行道，而其他道路則是雙向的。這對我們的東英格蘭交通系統有什麼影響

東英格蘭城鎮之間的加權道路

練習：帶標籤或加權圖 從 Maldon 到 Dunwich 的最短距離是多少？ 答案 Maldon 到 Tiptree = 8 Tiptree 到 Feering = 3 Feering 到 Blaxhall = 46 Blaxhall 到 Dunwich = 15 總計 = 72 現在此問題只有一個解決方案。 從 Harwich 到 Clacton 的最短距離是多少？ 答案 Harwich 到 Tiptree = 31 Tiptree 到 Clacton = 29 總計 = 60 從 Dunwich 到 Maldon 的最短距離是多少？ 答案 那個方向沒有直達路線

無向圖

無向圖不包含箭頭，沒有單行道。無向圖可以是加權的或未加權的

無向且未加權	無向且加權	無向且未加權
		一個簡單的圖，包含三個 頂點和三條邊。 每個頂點的度數為二， 因此這也是一個正則圖。

無向圖允許您沿每條邊雙向通行，它的工作方式與在每個頂點之間有兩條邊的有向圖相同。請參見上文中的 Blaxhall 和 Dunwich。

簡單圖

在定義簡單圖之前，我們需要了解迴圈和多重邊是什麼

• 迴圈是指一個頂點與其自身連線的邊
• 多重邊是指兩個頂點之間存在兩個或多個連線

簡單圖	非簡單圖
這是一個簡單圖，因為它沒有迴圈或多重邊	這不是一個簡單圖 上述示例中的迴圈是指某人從 Dunwich 出發散步，最終回到 Dunwich 而沒有訪問任何其他頂點。 Harwich 和 Blaxhall 之間存在多重邊，因為您可以乘渡輪或開車前往。

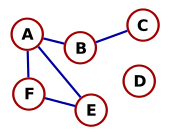
簡單圖 - 一個無向圖，沒有迴圈，並且任何兩個不同頂點之間最多隻有一條邊

在一個具有 n 個頂點的簡單圖中，每個頂點的度數都小於 n。

簡單圖
無迴圈、無多重邊、無方向

練習：簡單圖 給出簡單圖的定義 答案 它是一個無向圖，沒有迴圈，並且任何兩個不同頂點之間最多隻有一條邊。 以下哪些圖是簡單圖？ A B C D 答案 A B C D 否，因為它有一個迴圈（在 1 上） 是 否，因為它有一個多重邊（FN）並且是有向的 否，它是方向的

如何在計算機上儲存圖

到目前為止，我們已經瞭解瞭如何使用邊和頂點繪製圖。如果要將它們儲存為數字資料，則必須考慮一種對計算機友好的方式，因為計算機不擅長讀取手繪圖表。我們將研究兩種方法：鄰接矩陣和鄰接表。

鄰接矩陣

鄰接矩陣記錄每個頂點與所有其他頂點之間的關係。它同時記錄兩個頂點之間是否存在邊以及不存在邊的情況

無向-未加權	有向-未加權	無向-加權	有向-加權
B C D F H M T B 0 0 1 1 1 0 0 C 0 0 0 0 1 1 1 D 1 0 0 0 1 0 0 F 1 0 0 0 0 1 1 H 1 1 1 0 0 0 1 M 0 1 0 1 0 0 1 T 0 1 0 1 1 1 0	B C D F H M T B 0 0 1 0 0 0 0 C 0 0 0 0 1 1 0 D 1 0 0 0 0 0 0 F 1 0 0 0 0 1 0 H 1 0 1 0 0 0 1 M 0 0 0 0 0 0 1 T 0 1 0 1 0 0 0	B C D F H M T B ∞ ∞ 15 46 40 ∞ ∞ C ∞ ∞ ∞ ∞ 17 40 29 D 15 ∞ ∞ ∞ 53 ∞ ∞ F 46 ∞ ∞ ∞ ∞ 11 3 H 40 17 53 ∞ ∞ ∞ 31 M ∞ 40 ∞ 11 ∞ ∞ ∞ T ∞ 29 ∞ 3 31 ∞ ∞	B C D F H M T B ∞ ∞ 15 ∞ ∞ ∞ ∞ C ∞ ∞ ∞ ∞ 17 40 ∞ D 17 ∞ ∞ ∞ ∞ ∞ ∞ F 46 ∞ ∞ ∞ ∞ 11 ∞ H 40 ∞ 53 ∞ ∞ ∞ 31 M ∞ ∞ ∞ ∞ ∞ ∞ ∞ T ∞ 29 ∞ 3 ∞ ∞ ∞
兩個頂點之間存在邊 = 1 頂點之間不存在邊 = 0		兩個頂點之間存在邊 = 使用權重 頂點之間不存在邊 = ∞（無窮大符號）

優點

適用於邊多於節點的圖

缺點

不適用於邊少於節點的圖，因為它效率低下，會佔用大量記憶體

鄰接表

鄰接表記錄每個頂點與所有相關頂點之間的關係。它僅記錄兩個頂點之間是否存在邊。

無向-未加權	有向-未加權	無向-加權	有向-加權
連線到 Blaxhall D; H; F Clacton H; M; T Dunwich B; H Feering B; M; T Harwich B; C; D; T Maldon C; F; T Tiptree C; F; H; M	連線到 Blaxhall D Clacton H; M Dunwich B Feering B; M Harwich B; D; T Maldon T Tiptree C; F	連線到 Blaxhall D,15; H,40; F,46 Clacton H,17; M,40; T,29 Dunwich B,15; H,53 Feering B,46; M,11; T,3 Harwich B,40; C,17; D,53; T,31 Maldon C,40; F,11; T,8 Tiptree C,29; F,3; H,31; M,8	連線到 Blaxhall D,15 Clacton H,17; M,40 Dunwich B,17 Feering B,46; M,11 Harwich B,40; D,53; T,31 Maldon T,8 Tiptree C,29; F,3
列出每個連線		列出每個連線以及權重

優點

適用於邊數少於節點數的圖

缺點

不適用於邊數多於節點數的圖，因為它效率低下並佔用大量記憶體

練習：鄰接矩陣和鄰接表 為以下圖繪製鄰接表和鄰接矩陣 答案 A B C D E F A 0 1 0 0 1 1 B 1 0 1 0 0 0 C 0 1 0 0 0 0 D 0 0 0 0 0 0 E 1 0 0 0 0 1 F 1 0 0 0 1 0 連線到 A B; E; F; B A; C C B D E A; F F A; E 為以下圖繪製鄰接表和鄰接矩陣 答案 1 2 3 4 5 6 1 1 1 0 0 1 0 2 1 0 1 0 1 0 3 0 1 0 1 0 0 4 0 0 1 0 1 1 5 1 1 0 1 0 0 6 0 0 0 1 0 0 連線到 1 1; 2; 5 2 1; 3; 5 3 2; 4 4 3; 5; 6 5 1; 2; 4 6 4 為以下圖繪製鄰接表和鄰接矩陣 答案 1 2 3 4 1 0 1 0 1 2 0 0 0 1 3 1 1 0 0 4 0 0 1 0 連線到 1 2; 4 2 4 3 1; 2 4 3 為以下圖繪製鄰接表和鄰接矩陣 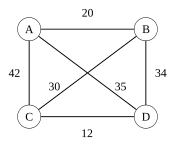答案 A B C D A ∞ 20 42 35 B 20 ∞ 30 34 C 42 30 ∞ 12 D 35 34 12 ∞ 連線到 A B,20; C,42; D,35 B A,20; C,30; D,34 C A,42; B,30; D,12 D A,35; B,34; C,12 為以下鄰接表繪製圖形 連線到 A B B A; C; D C B; D D B; C 答案 為以下鄰接表繪製圖形 連線到 A C,12; D,60 B A,10 C B,20; D,32 D B,22 E A,7 答案 為以下鄰接矩陣繪製圖形 A B D F N A 0 0 1 1 0 B 0 0 0 1 1 D 0 0 1 0 1 F 1 0 1 0 0 N 0 0 1 0 0 答案 為以下鄰接矩陣繪製圖形 A B D F N A ∞ 14 ∞ ∞ ∞ B ∞ ∞ 23 13 ∞ D 5 ∞ ∞ ∞ ∞ F 43 ∞ ∞ ∞ 33 N ∞ 22 ∞ 11 ∞ 答案 什麼時候你會使用鄰接表而不是鄰接矩陣？ 答案 對於連線數較少的圖，鄰接表佔用更少的空間。 什麼時候你會使用鄰接矩陣而不是鄰接表？ 答案 當圖有很多連線時，鄰接矩陣更可取。