計算理論：有限狀態機

有限狀態機

有限狀態機是一種抽象形式（為什麼/如何？）。它透過顯示系統可以處於的每個狀態以及每個狀態之間的轉換來模擬系統的行為。

考慮一臺電梯 

系統的可能狀態

'靜止在 1 樓'，'向上移動'，'靜止在 2 樓'，'向下移動'

[此處插入狀態圖片]

轉換及其輸入

• 從 '靜止在 1 樓' 到 '向上移動' 由 '向上按鈕' 觸發
• 從 '向上移動' 到 '靜止在 2 樓' 由 '到達 2' 觸發
• 從靜止在 2 樓到 '向下移動' 由 '向下按鈕' 觸發
• 從 '向下移動' 到 '靜止在 1 樓' 由 '到達 1' 觸發

從上面我們可以畫出電梯的有限狀態機。

[此處插入完成的有限狀態機圖片]

我們也可以製作一個狀態轉移表（定義這個語言框？）。

[此處插入狀態轉移圖圖片]

將系統表示為有限狀態機非常強大，因為該模型允許我們非常清楚地展示行為。我們可以證明該系統是健壯的，並且不會以任何意外的方式執行。考慮電梯的示例：透過將系統建模為有限狀態機，可以證明電梯無法在沒有停止的情況下向上和向下移動。這是因為設計清楚地表明，從狀態 '向上移動' 到狀態 '向下移動' 的轉換是不可能的。

有限狀態機在許多科學領域都有應用。主要是工程學、生物學，最常見的是語言學，它們被用來描述語言。

接受二進位制輸入的有限狀態自動機

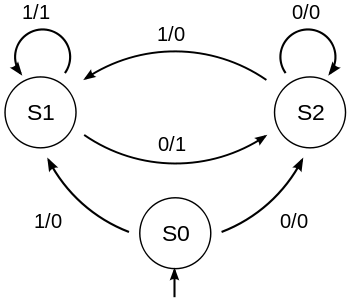
從上面的圖中我們可以看到它從狀態 S1 開始，輸入 1 將使其保持在狀態 S1，輸入 0 將使其移動到狀態 S2。一旦進入 S2，輸入 1 將使其保持在那裡，輸入 0 將使其切換回 S1。這意味著以下輸入是有效的

110011001
001110011

它似乎可以接受任何二進位制值，但事實並非如此。它唯一可以接受的狀態是狀態 S1。這給所有接受的輸入施加了以下規則：“包含偶數個零的二進位制數字組合”。這對於奇偶校驗很有用。如果我嘗試以下操作

110011011

我卡在狀態 S2 並且 FSM 沒有接受。你能建立一個 FSM 僅接受具有奇數個 1 的二進位制數字嗎？

練習：有限狀態自動機 對於上面的 FSM，以下哪些輸入是有效的 aaacdb ababacdaaac abcdb acda acdbdb 答案 aaacdb（正確） ababacdaaac（正確） abcdb（錯誤，沒有輸入可以接受 b 然後 c） acda（錯誤，S1 不是接受狀態） acdbdb（正確） 對於上面的 FSM，以下哪些輸入是有效的 987654321+994-0 5-5+2*4 9+8+7+6+5+4+3+2+1 0+1+2+1+ 99+88-77 答案 987654321+994-0（正確） 5-5+2*4（錯誤，沒有輸入 *） 9+8+7+6+5+4+3+2+1（正確） 0+1+2+1+（錯誤，S3 不是接受狀態） 99+88-77（正確） 繪製一個有限狀態自動機，它將接受單詞 Banana 同時僅使用 3 個狀態 答案 繪製一個單獨的有限狀態自動機，它將接受所有單詞 Tim Grit Grrrrrim 答案

米利機

米利機 - 帶有輸出的 FSM

一些 FSM 會根據狀態和輸入值輸出值

上面的米利機為每個輸入輸出一個值。你可以透過以下方式區分它們：輸入 / 輸出。因此對於以下輸入

000101010

它輸出

000010101

移位所有位到右邊，並將二進位制數字輸入除以二。

練習：米利機 對於上面的米利機，以下輸入會輸出什麼 50 20,10,20 10,10,10,20 這臺機器做什麼，輸出告訴你什麼？ 答案 0 30,20,0 40,30,20,0 這臺機器可以用來跟蹤進入自動售貨機的錢，讓你知道在購買 50 便士的巧克力棒時你還有多少錢要付 米利機和有限狀態自動機有什麼區別？ 答案 米利機輸出值 有限狀態自動機不輸出值

擴充套件：非確定性 在本節中，我們正在學習關於 確定性有限自動機。這意味著對於一個狀態和一個有效輸入，只有一個可能的轉換可以執行。存在 非確定性有限自動機，其中對於給定的輸入，可以執行多個路徑（或沒有路徑） 在狀態 p 中，對於輸入 1，有兩個可能的轉換

狀態轉移表

一個 狀態轉移表 跟蹤每個狀態和輸入。輸入通常放在左側，並與輸出分開，輸出放在右側。以下是一個簡單的示例，它包含一個具有兩個狀態的有限狀態機和一個二進位制輸入

輸入	當前狀態	下一個狀態	輸出
0	S1	S2	null
1	S1	S1	null
0	S2	S1	null
1	S2	S3	null

練習：狀態轉移表 為以下 FSM 建立一個狀態轉移表 答案 輸入 當前狀態 下一個狀態 輸出 0 S1 S2 null 1 S1 S1 null 0 S2 S1 null 1 S2 S2 null 為以下 FSM 建立一個狀態轉移表 答案 輸入 當前狀態 下一個狀態 輸出 0 S0 S2 0 1 S0 S1 0 0 S1 S2 1 1 S1 S1 1 0 S2 S2 0 1 S2 S1 0 為以下狀態轉移表繪製 FSM 輸入 當前狀態 下一個狀態 輸出 計時器 綠色 綠色 null 按鈕 綠色 黃色 null 計時器 黃色 紅色 null 計時器 紅色 綠色 null 答案 你可能已經注意到了。這代表一個交通燈系統 為以下狀態轉移表繪製 FSM 輸入 當前狀態 下一個狀態 輸出 a q0 q0 null b q0 q1 null a q1 q2 null b q1 q1 null a q2 q1 null b q2 q1 null 答案