資料表示基礎:無符號二進位制算術
您應該熟悉十進位制中的加減乘法。計算機需要在二進位制中執行相同的操作,您需要在考試中瞭解它!
讓我們來看一個十進位制加法的例子
25 +43 --- 68
這很簡單,我們只需將每列加起來,但如果結果不能放入一列中會發生什麼?我們需要使用進位位
98 +57 --- 155 11
希望您對這方面很熟悉。現在讓我們看一下它如何在二進位制中完成,並使用一個非常簡單的例子,並在十進位制中進行檢查
01010 (1010) +00101 (510) ------ 01111 (1510)
這看起來非常簡單,但當我們有進位位時會發生什麼?與十進位制中幾乎相同
01011 (1110) +00001 (110) ------ 01100 (1210) 11

|
練習:二進位制加法 1010 + 0001 答案 1010 +0001 ---- 1011 01001001 + 00110000 答案 01001001 +00110000 -------- 01111001 01010100 + 00110000 答案 01010100 +00110000 -------- 10000100 01001010 + 00011011 答案 01001010 +00011011 -------- 01100101 01111101 + 00011001 答案 01111101 +00011001 -------- 10010110 00011111 + 00011111 答案 00011111 +00011111 -------- 00111110 10101010 + 01110000 答案 10101010 +01110000 -------- 100011010 Note we have some overflow, this will come in useful when doing subtraction |
希望您在小學的時候已經學會了如何在十進位制中將數字相乘。讓我們回顧一下
12 x 4 -- 8 = 4*2 40 = 4*10–48
以及一個更復雜的例子
12 x14–8 = 4 * 2 40 = 4 * 10 20 = 10* 2 100 = 10* 10–168
二進位制也是同樣的原理。讓我們來看一個例子
101 x 10 ---- 0 = 0 * 101 1010 = 10 * 101 [or in denary 2 * 5 = 10]
讓我們嘗試一個更復雜的例子
1011 [11] x 111 [7] ---- 1011 = 1 * 1011 10110 = 10 * 1011 101100 = 100 * 1011 ------ now add them together 1001101 = [77 double check with the decimal earlier]
|
練習:二進位制乘法 101 * 10 答案 101 x 10 ---- 1010 11 * 11 答案 11 x 11 ---- 11 110 ---- 1001 1011 * 101 答案 1011 x 101 ------ 1011 101100 ------ 110111 1111 * 111 答案 1111 = 15
x 111 = 7
------
1111
11110
111100
------
1101001 = 105
如果將一個二進位制數乘以 2,它會向左移動多少位? 答案 1 如果將一個二進位制數乘以 16,它會向左移動多少位? 答案 4(因為 2^4 = 16) 這是計算機中乘法的快捷方式,它使用機器程式碼移位指令來執行此操作。不用擔心,您不需要了解本課程大綱的這些內容 |
|
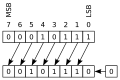
擴充套件:位移位 如果您檢視以下數字的二進位制表示,您可能會注意到一些奇怪的事情 0001 = 1 0010 = 2 0100 = 4 1000 = 8 每次我們將數字向左移動一位時,數字的值就會加倍。這不僅適用於一位,請檢視這個更復雜的例子。 0001 0101 = 21 0010 1010 = 42 同樣,向左移動一位,數字就加倍。另一方面,向右移動一位會將值減半。 計算機在進行乘法和除法方面 notoriously 糟糕,它需要大量的 CPU 時間,並且會嚴重降低程式碼速度。為了解決這個問題,計算機可以在暫存器中移動值,只要乘法或除法是 2 的冪,那麼 CPU 時間就會減少,因為操作只需要一行機器程式碼。處理器可以執行幾種型別的 移位
向左或向右移動,您會在空的一端新增一個 0。
您將保持被移動數字的符號位。 請注意,邏輯移位示例也是算術移位示例,因為符號保持不變。您將在學習補碼時瞭解符號位
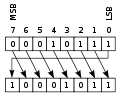
被推到一端的位出現在另一端
|