A-level 數學/OCR/D1/節點圖/介紹
本節討論節點圖,有時也稱為圖或網路。
首先,我們必須說明我們對圖的理解。一個圖是由點(我們稱之為節點或頂點)和連線這些點的線(弧或邊)組成的集合。在思考圖時,每條弧的長度和佈局並不重要,重要的是哪些頂點連線到哪些其他頂點。
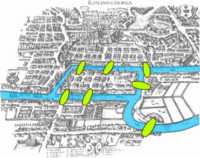
哥尼斯堡七橋問題,或稱哥尼斯堡橋問題,是一個經典問題,是圖論中的第一個問題之一。它是由普魯士哥尼斯堡(今俄羅斯加里寧格勒)這座城市的實際佈局引發的。
上面是這座城市的示意圖,河流用藍色表示,橋樑用綠色表示。問題是,是否有可能從城市中的某個地方出發,穿過每座橋一次且僅一次,並回到起點。數學家萊昂哈德·尤拉(1707-1783)設法解決了這個問題,他專注於重要的方面。他意識到,重要的是哪些地方相連,以及相連多少次,而不是每座橋的長度或佈局。換句話說,這個問題可以用圖來表示。下面是一個這樣的表示
在這個圖中,紅色的點是頂點,代表河流的每條岸以及中間的兩個島嶼。它們之間的線和曲線是弧,代表橋樑。尤拉對這個問題的解決方案在這個抽象的表示中更容易理解。他發現不可能只走一次就遍歷每座橋,原因如下
當行人穿過橋樑時,他們在訪問的每個地方(除了起點和終點之外)必須成對進出。也就是說,如果他們訪問一次,他們就進入,然後離開,如果兩次,他們就進入兩次,離開兩次,依此類推。這意味著,由於每次進出都必須經過不同的橋樑,而且所有橋樑都必須使用,因此除了路線的起點和終點之外,從每個點出發的橋樑數量必須是偶數。起點和終點一般來說可以是例外,因為行人從一個地方離開而不進入,進入另一個地方而不離開,所以從它們那裡出發的橋樑數量將是奇數。但是,如果起點和終點相同,如這裡要求的那樣,那麼進出就會再次配對,因此所有點都必須有偶數個橋樑從它們那裡出發。
概括地說,如果每個點都有偶數個橋樑,那麼這樣的路線就是可能的。這意味著在哥尼斯堡七橋問題的情況下,不可能按順序遍歷每座橋一次且僅一次,因為每個點都有奇數個橋樑從它出發。即使從不同的地點開始和結束也不可能。
尤拉對哥尼斯堡七橋問題的解決方法得出了一個適用於所有圖的結果。然而,在我們看到這個結果之前,我們需要一些更多的術語。
首先,尤拉路徑是在圖中從一個頂點到另一個頂點的路線,使用圖中的所有邊。歐拉回路是一條尤拉路徑,其中起點和終點相同。這相當於這個問題中要求的。根據這些術語,如果存在歐拉回路,則圖是尤拉圖,如果存在尤拉路徑但不是迴路,則圖是半尤拉圖。最後,頂點的度數是從它出發的邊的數量。
上面的結果表明,一個圖只有當所有頂點的度數都是偶數時,才是尤拉圖。換句話說,每個頂點的度數必須是偶數。後來證明,任何所有頂點的度數都是偶數的圖都是尤拉圖。類似地,當且僅當一個圖只有 2 個頂點的度數是奇數時,它才是半尤拉圖。
下面是一些圖的示例,這些示例說明了如何判斷一個圖是尤拉圖還是半尤拉圖
-
示例一
-
示例二
-
示例三
-
示例四
示例一是一個既不是尤拉圖也不是半尤拉圖的圖,因為有四個頂點的度數是奇數,而不是要求的零(對於尤拉圖)或兩個(對於半尤拉圖)。
示例二和示例三是半尤拉圖,因為只有兩個頂點的度數是奇數。
示例四是尤拉圖,因為所有頂點的度數都是偶數。
現在我們知道如何判斷尤拉路徑或迴路是否存在。然而,我們還沒有一個生成這種路徑的方法。弗勒裡演算法是一種保證在存在尤拉路徑或迴路時提供這種路徑或迴路的方法。該方法如下
- 選擇任何度數為奇數的頂點。如果沒有,則選擇任何頂點。
- 從該頂點選擇任何一條邊,我們可以從圖中刪除它而不使其斷開連線。換句話說,當我們刪除這條邊時,我們仍然可以從任何頂點到達任何其他頂點。
- 穿過這條邊,並將其從圖中刪除。
- 刪除任何沒有從它們出發的邊的頂點。
- 如果還有邊要穿過,則返回步驟 2。
如果我們遵循這種方法,我們將會遵循一條尤拉路徑或試驗,前提是存在一條尤拉路徑。保持圖連線的條件消除了我們將圖分成兩個“島嶼”的可能性,最終被困在一個島嶼上,沒有未使用的邊可以回到另一個島嶼。我們可以留下“孤立的”頂點,沒有從它們出發的邊,因為沒有邊可以從它們出發或到達它們進行遍歷。這就是為什麼我們可以刪除它們的原因。
沒有尤拉路徑會像描述的那樣分割圖,所以任何尤拉路徑都必須透過使用該演算法來形成。
可能需要在此處定義更多術語。