人工神經網路/啟用函式

啟用函式

神經網路中使用了許多常見的啟用函式。這不是一個詳盡的列表。

階躍函式

階躍函式類似於原始感知器中使用的函式。如果輸入和超過某個閾值，則輸出為某個值 A₁；如果輸入和低於某個閾值，則輸出為 A₀。感知器中使用的值為 A₁ = 1 和 A₀ = 0。

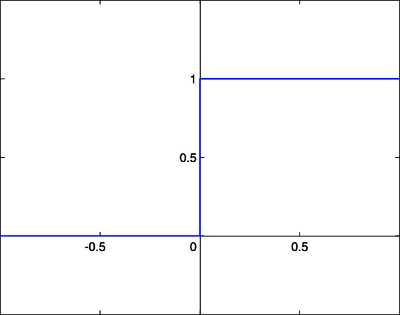
這些型別的階躍啟用函式對於二元分類方案很有用。換句話說，當我們想要將輸入模式分類到兩個組中的一個時，可以使用具有階躍啟用函式的二元分類器。另一個用途是建立一組小的特徵識別器。每個識別器都是一個小的網路，如果存在特定的輸入特徵，則輸出 1，否則輸出 0。將多個特徵檢測器組合到一個網路中，可以解決非常複雜的聚類或分類問題。

線性組合

線性組合是指神經元的加權和輸入加上線性相關的偏置成為系統輸出。具體來說

$y=\zeta +b$

在這些情況下，輸出的符號被認為等同於階躍函式系統的 1 或 0，如果

$\theta =-b$.

連續Log-Sigmoid函式

Log-Sigmoid函式，也稱為邏輯函式，由以下關係給出

$\sigma (t)={\frac {1}{1+e^{-\beta t}}}$

其中 β 是斜率引數。這被稱為 log-sigmoid，因為也可以使用雙曲正切函式而不是這種關係來構造 sigmoid，在這種情況下，它將被稱為 tan-sigmoid。在這裡，我們將 log-sigmoid 簡稱為“sigmoid”。sigmoid 具有類似於階躍函式的特性，但增加了不確定區域。在這方面，sigmoid 函式非常類似於生物神經元的輸入-輸出關係，儘管並不完全相同。以下是 sigmoid 函式的圖形。

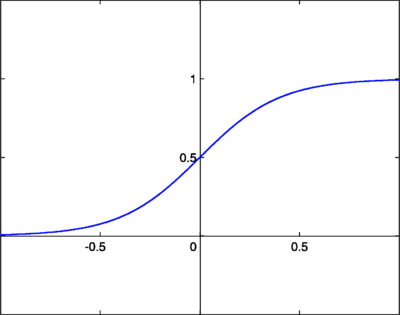
sigmoid 函式也很受歡迎，因為它們的導數很容易計算，這有助於在某些訓練演算法中計算權重更新。當$\beta =1$時的導數由下式給出

${\frac {d\sigma (t)}{dt}}=\sigma (t)[1-\sigma (t)]$

當$\beta \neq 1$時，使用$\sigma (\beta ,t)={\frac {1}{1+e^{-\beta t}}}$，導數由下式給出

${\frac {d\sigma (\beta ,t)}{dt}}=\beta [\sigma (\beta ,t)[1-\sigma (\beta ,t)]]$

連續Tan-Sigmoid函式

$\sigma (t)=\tanh(t)={\frac {e^{t}-e^{-t}}{e^{t}+e^{-t}}}$

其導數為

${\frac {\operatorname {d} \sigma (t)}{\operatorname {d} t}}=1-\tanh ^{2}(t)=\operatorname {sech} ^{2}(t)=1-{\frac {(e^{t}-e^{-t})^{2}}{(e^{t}+e^{-t})^{2}}}$

ReLU：線性整流函式

ReLU啟用函式定義為

$\sigma (t)=\max(0,t)$

它也可以用分段函式表示

$\sigma (t)={\begin{cases}0&{\text{if }}t<0\\t&{\text{if }}t>0\end{cases}}$

ReLU啟用函式

其導數為

$\sigma (t)={\begin{cases}0&{\text{if }}t<0\\1&{\text{if }}t>0\end{cases}}$

ReLU 最初由 Fukushima Kunihiko 於 1969 年為影像的表示學習引入，現在是深度學習中最流行的啟用函式。它具有非常簡單的公式和導數，使得反向傳播計算更容易計算。由於導數函式的輸出對於正輸入始終為 1，因此與其他啟用函式相比，它不太容易受到梯度消失或爆炸問題的影響。ReLU確實存在“死亡 ReLU”的獨特問題，其中某些節點可能很少啟用或“死亡”，無法為模型提供預測能力。為了避免死亡 ReLU 問題，引入了 Leaky ReLU 和 Parametric ReLU 等 ReLU 變體。

Softmax 函式

Softmax 啟用函式主要在聚類系統的輸出層中使用。Softmax 函式將原始值轉換為後驗機率。這提供了一種確定性度量。Softmax 啟用函式表示為

$y_{i}={\frac {e^{\zeta _{i}}}{\sum _{j\in L}e^{\zeta _{j}}}}$

L 是輸出層中神經元的集合。