組合語言與計算機組成/引言和概述

本章介紹了計算機體系結構和計算機算術的基礎知識。

計算機的功能

為了探究計算機如何運作，我們首先要弄清楚計算機究竟在做什麼。毫無疑問，你對計算機的功能有所瞭解。畢竟，很可能你現在正在用電腦閱讀這篇文章！如果我們試圖列出計算機的所有功能，我們將得到一個驚人的複雜的功能和特性組合。相反，我們需要做的是剝開所有功能層，看看後臺發生了什麼。

基本計算機

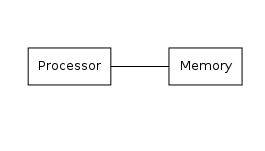
如果我們從最抽象的層面上看待一臺計算機，它們所做的事情就是處理資訊。我們可以將這種抽象的機器表示為某種儲存器和某種處理器。處理器可以根據指令列表讀取和寫入儲存器中的專案，而儲存器只是記住它接收到的資料。處理器執行的指令列表被稱為計算機程式。這種安排如何實現的細節決定了計算機本身的性質。使用這種定義，相當廣泛的裝置可以被歸類為計算機。我們稱之為“計算機”的大多數裝置實際上都是通用計算機。也就是說，如果給它們無限的儲存器，它們將能夠計算任何可計算的函式。通用計算機的要求實際上非常簡單。基本上，一臺機器是通用的，如果它能夠執行以下操作

1. 從記憶體中讀取一個值。
2. 根據讀取的值，確定一個新的值寫入記憶體。
3. 根據讀取的值，確定下一個要執行的指令。

遵循這些規則的機器被稱為“圖靈完備”。圖靈完備的完整定義超出了本書的範圍。如果你感興趣，請參閱關於圖靈機和圖靈完備性的文章。

試圖根據通用計算機的約束條件來建立程式將非常困難。建立更實用的指令列表會更方便，例如“加”、“減”、“乘”和“除”。處理器可以執行的指令列表被稱為機器的指令集。該指令集有助於定義機器的行為，並進一步定義將在機器上執行的程式的性質。

機器的另一個決定性特徵回答了“程式儲存在哪裡？”這個問題。你會注意到，在我們對基本計算機的圖示中，我們沒有顯示程式位於何處。這樣做是有目的的，因為回答這個問題有助於定義不同型別的計算機。進一步分解系統的元件是下一節的主題。

計算機體系結構

計算機的另一個決定性特徵是系統的邏輯佈局。這個屬性被稱為計算機的體系結構。計算機體系結構描述了機器如何邏輯組織以及它的指令集是如何實現的。設計計算機時，最重大的架構決策之一是如何組織它的記憶體，以及如何將程式載入到機器中。在計算機早期歷史中，儲存程式計算機和硬連線計算機之間存在區別。例如，第一臺通用電子計算機 ENIAC 是透過將機器的單元連線到稱為功能表的裝置來程式設計的。後來的機器，如 EDSAC，將程式作為資料儲存在程式記憶體中。當然，儲存程式被證明更加方便。與簡單地將新資料載入到機器中相比，重新連線一臺機器需要的時間太長了。在當今的計算時代，幾乎所有計算機都是儲存程式計算機。在這本書中，我們將重點關注儲存程式計算機體系結構。

確定了將程式作為資料儲存後，我們現在必須將注意力轉向程式在記憶體中儲存的位置和方式。在過去，人們提出了許多不同的解決方案，但今天主要有兩個高層變體。它們是馮·諾依曼體系結構和哈佛體系結構。

馮·諾依曼體系結構

馮·諾依曼體系結構是當今存在的最常見的體系結構。PC、Mac 甚至 Android 手機都是馮·諾依曼計算機的例子。

馮·諾依曼體系結構是一種儲存程式計算機，它包含以下元件

1. 一個 CPU（中央處理單元），它執行程式指令。
2. 一個記憶體，它同時儲存程式和資料。
3. 輸入和輸出裝置

馮·諾依曼體系結構的決定性特徵是資料和指令都儲存在同一個記憶體裝置中。程式被儲存為 CPU 解碼以執行指令的二進位制模式集合。當然，資料也被儲存為記憶體中的位模式。CPU 只能透過在記憶體中遇到資料的上下文來區分資料和程式程式碼。這種體系結構中的 CPU 從某個記憶體位置開始執行指令，並繼續逐步執行指令。在遍歷程式時遇到的任何內容都被視為程式指令。當 CPU 收到讀取或寫入記憶體資料的指令時，CPU 會將記憶體中的數字視為資料。當然，這也意味著馮·諾依曼機器完全能夠修改自己的程式。

計算機算術

計算機花費大量時間計算簡單的算術表示式。事實上，如果我們從“計算”的角度思考，算術就是首先想到的。因此，計算機如何處理數字是計算機體系結構研究的重要組成部分。第一臺電子計算機 ENIAC 使用與人類相同的方式表示數字，使用十進位制算術及其運算。這種方法的問題在於，你必須有 10 個可區分的狀態（0 到 9），這大大增加了操作它的機器的複雜性。表示和區分 10 個狀態需要非常精確的電子裝置。如果我們想用電子裝置製作簡單的表示，最簡單、最容易區分的是兩個狀態“開”和“關”。這不需要那麼精確的檢測和傳播，因此它極大地簡化了機器的物理實現，但是它確實引出了“如何用只有兩個符號來進行數學運算？”的問題。

答案是我們使用二進位制數系統，其中這些狀態對映到 0 和 1。所以我們可以將 0 視為“關”，將 1 視為“開”。本節將解釋這個數字系統是如何工作的，並介紹表示這些數字的方便方法。

數字的表示和基數

為了理解二進位制，我們需要首先了解整數本身的性質。我們必須稍微深入一下數論的領域，但我保證它不會很痛苦！我們從一個簡單的例子開始。你在下面看到了什麼？

$145$

換句話說，你可能會說這是數字“一百四十五”。然而，這並不準確。你真正看到的是這個數量的表示。從小學開始，你就被教導了一種特定的寫數字的方法。這個系統被稱為“十進位制”或“十進位制”數系。當你看到“145”時，你實際上是在看到一種約定，其中

$145=1\cdot 100+4\cdot 10+5\cdot 1$

注意，這些項都是十的冪。因此我們可以將其改寫為

$145=1\cdot 10^{2}+4\cdot 10^{1}+5\cdot 10^{0}$

口語化地說，我們稱數字中的位置為“個位、十位和百位”。如果我們繼續下去，每個位置的十的冪都比前一個位置大 1。因此我們可以構建一個表格，我相信你以前肯定見過。

${\begin{array}{|c|r|l|}\hline {\textrm {Exponent}}&{\textrm {Number}}&{\textrm {PlaceName}}\\\hline 10^{0}&1&{\textrm {Ones}}\\10^{1}&10&{\textrm {Tens}}\\10^{2}&100&{\textrm {Hundreds}}\\10^{3}&1,000&{\textrm {Thousands}}\\10^{4}&10,000&{\textrm {TenThousands}}\\10^{5}&100,000&{\textrm {HundredThousands}}\\\hline \end{array}}$

當然，我們可以透過簡單地增加指數來無限地繼續下去，新增新的位置值。我們可以用十進位制系統推廣這一點，說一個由$k$ 個數字組成的序列的值用一個多項式表示為

$\langle d_{k}\ldots d_{2}d_{1}d_{0}\rangle =\sum _{i=0}^{k}10^{i}$

注意，我們可以用任何任意的數字基數來表達這一點。因此，我們可以對上述內容進行推廣，說對於一個任意的基數 $b$，一個由$k$ 個數字組成的序列的值是

$\langle d_{k}\ldots d_{2}d_{1}d_{0}\rangle =\sum _{i=0}^{k}b^{i}$

這為表示數字提供了許多可能性。你可以選擇你喜歡的任何任意的基數。你使用的數值基數決定了用於表示數字的符號以及如何解釋這些符號。一般來說，對於一個基數 $b$，我們必須有 $b$ 個符號來表示它。對於十進位制，我們有 10 個符號 (0, 1, 2, 3, 4, 5, 6, 7, 8, 9)。注意，每個位置中使用的最高值符號的值是 $b-1$。因此，只要我們有一組符號來支援它，我們就可以使用任何我們選擇的數字基數。

二進位制數

現在我們可以將注意力轉向與“開”和“關”兩種易於識別的狀態相匹配的數字基數。這就是二進位制或以 2 為基數的數字系統。從上面的觀察中，二進位制數字系統只包含符號 (0, 1)。它的“位置”定義如下表所示

${\begin{array}{|c|r|l|}\hline {\textrm {Exponent}}&{\textrm {Number}}&{\textrm {PlaceName}}\\\hline 2^{0}&1&{\textrm {Ones}}\\2^{1}&2&{\textrm {Twos}}\\2^{2}&4&{\textrm {Fours}}\\2^{3}&8&{\textrm {Eights}}\\2^{4}&16&{\textrm {Sixteens}}\\2^{5}&32&{\textrm {Thirty-Twos}}\\2^{6}&64&{\textrm {Sixty-Fours}}\\2^{7}&128&{\textrm {OneHundredTwentyEights}}\\\hline \end{array}}$

就像十進位制一樣，我們可以透過簡單地增加指數將此繼續到無窮大。我在 8 位後停止了，因為正如我們將在後面看到的，這是我們在計算機中經常使用的單位。所以，假設我們有以下二進位制數

$10010001$

我們如何確定它的值？請記住，這遵循與十進位制數相同的規則，因此從左到右，我們可以將此數轉換為十進位制數，如下所示：

$1\cdot 128+0\cdot 64+0\cdot 32+1\cdot 16+0\cdot 8+0\cdot 4+0\cdot 2+1\cdot 1=145$

現在我們已經瞭解瞭如何將二進位制（或任何進位制數）轉換為十進位制，您可能想知道我們如何進行另一個方向的轉換。也就是說，如何將十進位制數轉換為二進位制（或任何任意進位制）。答案很簡單。我們可以透過反覆除以目標進位制來將十進位制數轉換為任何進位制數。每個除法的餘數從右到左表示轉換後的數字的位數。證明為什麼這有效留給讀者作為練習。讓我們透過將我們的好朋友 145 轉換為二進位制來測試一下。

${\begin{aligned}145\div 2&=&72~&R=1\\72\div 2&=&36~&R=0\\36\div 2&=&18~&R=0\\18\div 2&=&9~&R=0\\9\div 2&=&4~&R=1\\4\div 2&=&2~&R=0\\2\div 2&=&1~&R=0\\1\div 2&=&0~&R=1\\\end{aligned}}$

請注意，一旦商為 0，我們就可以停止，因為它將從這裡開始一直保持為 0。因此，我們可以透過以相反的順序讀取餘數來讀取二進位制數

$10010001$