天體力學/經典軌道要素

天體力學

軌道引數

可以使用一組 5 個引數完全指定軌道。利用這 5 個引數，我們可以精確地指定軌道的方位、在 3 維空間中的方向以及大小。如果我們有一個可選的第六個引數，我們可以確定衛星在任意時間 t 的軌道上的確切位置。這 6 個引數稱為開普勒要素。

然而，在我們討論這 6 個軌道引數之前，我們需要引入一些新的術語。

角動量

從地球中心指向衛星或感興趣物體的向量稱為 r，其速度向量稱為 v。垂直於這兩個向量的向量稱為 比角動量 向量。

[角動量]

$\mathbf {h} =\mathbf {r} \times \mathbf {v}$

升交點

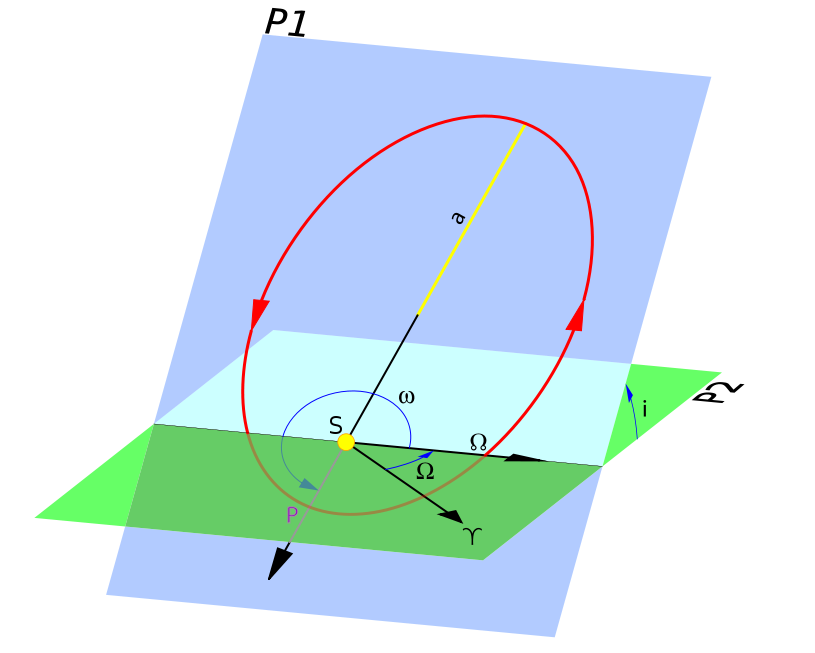
地球赤道位於一個稱為 基本平面 的平面內（因為它位於地心-赤道座標系中，我們將在本節中使用），而向量 r 所描繪的軌道形成一個稱為 軌道平面 的平面，它包含向量 r 和 v。這兩個平面的交線稱為 節點線。

我們可以透過對角動量向量 h 和單位向量 K = <0, 0, 1> 取叉積來找到向量 n。

[升交點]

$\mathbf {n} =\mathbf {K} \times \mathbf {h}$

n 是節點線上指向 升交點 方向的向量。升交點是衛星以北方向穿過赤道的點。同樣，降交點是衛星以南方向穿過赤道的點。

在赤道軌道中，n 未定義，並且沒有節點。

順行和逆行

順行 或直接表示衛星繞地球從西向東執行。逆行 表示衛星從東向西執行。傾角在 0 到 90 度之間的物體以與主天體自轉相同的方向繞其執行。傾角正好為 90 度的物體具有垂直軌道，既不是順行也不是逆行。傾角在 90 度到 180 度之間的物體處於逆行軌道。

視覺表示

此影像顯示了兩個平面，軌道平面（淡黃色）和參考平面（灰色）。地球或主焦點被認為位於兩個平面的中心的點。請注意，軌道如何在兩個點處與黃道相交：一次是向北（升交點），一次是向南（降交點）。降交點在此影像中未標記，但其位置應該很明顯。我們將在下面解釋其他一些術語。

經典要素

現在我們有了節點向量，以及向量 r、v 和 h，我們可以找到我們的 5 個經典軌道要素。

半長軸

半長軸 a 可以透過 Vis-Viva 方程求得

$a=-{\frac {\mu }{2{\mathcal {E}}}}=-{\frac {\mu }{2}}\left[{\frac {v^{2}}{2}}-{\frac {\mu }{r}}\right]^{-1}$

其中一些術語仍然未定義。

偏心率

偏心率 e 可以透過偏心率向量的幅值確定

[偏心率向量]

$\mathbf {e} =\left({\frac {v^{2}}{\mu }}-{\frac {1}{r}}\right)\mathbf {r} -{\frac {\left(\mathbf {r} \cdot \mathbf {v} \right)}{\mu }}\mathbf {v}$

或者，它可以表示為

[偏心率]

$e={\sqrt {1+{\frac {2{\mathcal {E}}h^{2}}{\mu ^{2}}}}}$

儘管偏心率向量將在計算後續要素時需要。

傾角 ($i$)

傾角i是K單位向量與角動量向量h之間的夾角。它可以使用以下公式計算：

[軌道傾角]

$i=\arccos {\frac {h_{K}}{h}}$

傾角始終小於180°。

升交點赤經 ($\Omega$)

升交點赤經Ω是升交點與I單位向量之間的夾角。它可以計算為

[升交點赤經]

$\Omega =\arccos {\frac {n_{I}}{n}}$

如果n_J分量大於零，則Ω小於180°。否則，Ω大於180°。

近心點幅角 ($\omega$)

近心點幅角是軌道平面內升交點與近心點之間的夾角。我們可以計算它為

[近心點幅角]

$\omega =\arccos {\frac {\mathbf {n} \cdot \mathbf {e} }{ne}}$

如果e_K大於0，則ω小於180°。否則，ω大於180°。

近心點透過時間

近心點透過時間是衛星到達近心點的時間。我們將此時間定義為T_p。它可以從觀測中確定。這是第六個軌道引數，它允許計算天體在任何時間的位置。

可選要素

近心點赤經 ($\Pi$)

近心點赤經是升交點赤經和近心點幅角之和

[近心點赤經]

$\Pi =\Omega +\omega$

曆元真近點角 ($\nu _{0}$)

曆元真近點角是從近心點到衛星在曆元T₀處的半徑向量的角度，表示為$\nu _{0}$

曆元緯度幅角 ($u$)

曆元緯度幅角是升交點與衛星在曆元處的夾角

$u=\nu +\omega$

真經度在曆元 ($l$)

真經度在曆元是參考方向（通常是春分點 ♈）與衛星位置之間的角度。它從參考方向到升交點（如果存在）在參考平面測量，然後從升交點到衛星在軌道平面上的位置測量。

$l=\Omega +\omega +\nu =\Pi +\nu =\Omega +u$

尋找 r 和 v

從五個經典軌道要素，我們可以確定 r 和 v。

$\mathbf {r} =r\cos(\nu )\mathbf {P} +r\sin(\nu )\mathbf {Q}$

$\mathbf {v} ={\sqrt {\frac {\mu }{p}}}[-sin(\nu )\mathbf {P} +e\mathbf {Q} +\cos(\nu )\mathbf {Q} ]$

其中 P 和 Q 是近心座標系中的單位向量。使用我們的座標轉換，我們可以將其轉換為地心赤道座標。