天體力學/軌道基礎
軌跡方程,它給出軌道的形狀,表示為
[軌跡方程]
其中B是積分常數,ν(希臘字母nu)是半長軸和位置向量r之間的角度。
讓我們稍微偏離軌道的理論,並討論圓錐曲線。人們通常熟悉圓錐曲線(圓、橢圓、拋物線、雙曲線),這些曲線是從研究初等代數中得來的。但是,大多數人不熟悉圓錐曲線的形式是在標準笛卡爾座標系中。如果我們使用極座標系,我們可以看到所有的圓錐曲線都有類似的方程格式。我們可以概括地說,所有圓錐曲線都有以下極座標方程
[圓錐曲線方程]
這裡,r是半徑,θ是角度。當θ圍繞圓圈移動時,r的值會發生變化,結果產生的點會建立所需的圓錐曲線。變數p被稱為引數,變數e被稱為偏心率。我們將討論這些變數,並描述它們如何與下面的軌跡方程相關。
比較軌跡方程和圓錐曲線方程,我們可以看到
變數p是圓錐曲線大小的度量。較大的p表示軌道更大。我們可以看到軌道的尺寸與衛星的角動量成正比。由於這種關係,我們可以大致瞭解到,衛星的速度越快,產生的軌道就越大。
e的值,即偏心率,決定了軌道將採用的形狀。此表顯示了e的各種值,以及由此產生的圓錐曲線的形狀
| e | 形狀 |
|---|---|
| 圓形 | |
| 橢圓形 | |
| 拋物線形 | |
| 雙曲線形 |
檢視我們的圓錐曲線方程和軌跡方程,我們可以看到
我們知道B只是一個積分常數,它不對應任何自然量。我們可以直接計算e,而無需先計算B。我們可以透過以下公式將e與衛星的能量和角動量聯絡起來
我們也可以使用半長軸的長度a將e和p聯絡起來
我們還可以定義一個偏心向量 e,表示為
[偏心向量]
該向量具有以下性質
並且 e 指向近心點(下面將介紹)。
軌道
[edit | edit source]我們可以看到,軌道方程的形式是圓錐曲線,由於這種形式,實際上可以有各種圓錐曲線形狀的軌道。下面我們將討論其中的一些。
橢圓軌道
[edit | edit source]橢圓軌道是偏心率 e < 1 的軌道。橢圓軌道是最常見的軌道之一,幾乎所有繞太陽執行的天體都具有橢圓軌道。
我們從 p 的方程知道,衛星的速度會影響軌道的尺寸。我們還從 p 和 e 之間的關係方程知道,速度可以影響軌道的形狀。因此,將衛星送入特定的軌道,需要賦予衛星與該軌道對應的正確速度。橢圓軌道是由低於逃逸速度的速度產生的軌道。逃逸速度,我們將在下面討論,是指衛星擺脫主焦點的引力並形成拋物線或橢圓軌道的速度。
有一個特定的速度被稱為圓周速度,在該速度下,橢圓軌道會變成完美的圓形。除圓周速度之外,所有其他速度,只要低於逃逸速度,都會產生橢圓軌道。
可以透過將適當的值代入軌道方程來建立所需的圓錐曲線,然後求解動能,來計算這些速度的值。這裡將省略推導過程。
示例:地球的軌道
地球的軌道是橢圓的,儘管兩個焦點距離相對較近,使得地球的軌道幾乎是圓形的。因為太空是真空,沒有明顯的阻力或摩擦,地球的速度是恆定的,因此地球的軌道也是恆定的。從數學上來說,地球永遠不會螺旋狀地落入太陽。
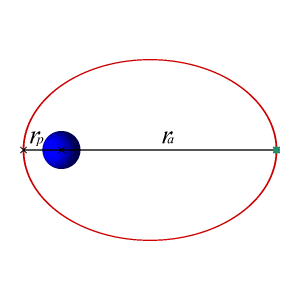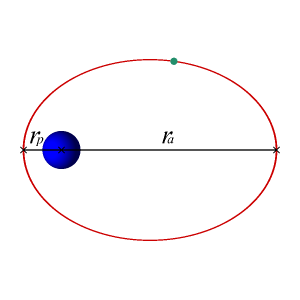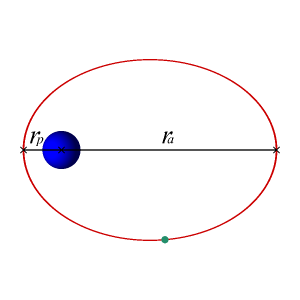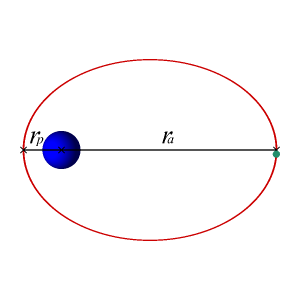
圓形軌道
[edit | edit source]圓形軌道是偏心率 e = 0 的軌道。圓形是橢圓的一種特殊情況。圓形軌道很難獲得,但並非不可能。維持圓形軌道所需的速度被稱為圓周速度。我們可以將圓周速度定義為
[圓周速度]
這裡 r 表示圓形軌道的半徑。
拋物線軌道
[edit | edit source]拋物線軌道是偏心率 e = 1 的軌道。形成拋物線軌道所需的速度被稱為逃逸速度 ve。逃逸速度是擺脫主焦點的引力所需的最小速度。請注意,當我們獲得這個最小逃逸速度時,我們將擺脫主焦點的引力,但我們的速度將接近零
我們可以將逃逸速度定義為
[逃逸速度]
在本例中,r 表示衛星到主焦點的距離,ver 表示從點 r 出發的逃逸速度。對於地球,該速度等於第二宇宙速度,即 11.1799 公里/秒。

雙曲線軌道
[edit | edit source]雙曲線軌道具有偏心率 e > 1。雙曲線軌道有時也稱為逃逸軌道,因為雙曲線軌道允許衛星從主焦點的引力中“擺脫”,同時保持一定的速度。衛星比拋物線軌道的逃逸速度多出的速度被稱為“雙曲線超額速度”,vh,可以透過與發射速度(或近心點速度)vl 進行比較來找到。
與拋物線軌道相比,我們的最終速度為

退化
[edit | edit source]熟悉圓錐曲線的人可能會認識到,還有退化的圓錐曲線:點和直線。退化的圓錐曲線出現在 h = 0 的情況下,這意味著 e = 1(拋物線),但軌道將不是拋物線。
拱點
[edit | edit source]連線焦點的直線被稱為長軸(在橢圓和雙曲線中)。曲線與長軸交點的點被稱為拱點。最靠近主焦點的點稱為近心點,最靠近次焦點的點稱為遠心點。還有其他幾個詞可以互換使用
| 中心天體 | 最短距離 | 最遠距離 |
|---|---|---|
| 一般 | 近心點/近心點 | 遠心點/遠心點 |
| 地球 | 近地點 | 遠地點 |
| 太陽 | 近日點 | 遠日點 |
其他太陽系天體也存在附加術語,但對於本文的目的來說,這些術語不需要。
圓形沒有離中心最遠或最近的點,因此近心點和遠心點在圓形上是未定義的。拋物線有一個近心點,但遠心點被認為在無窮遠處。
從主焦點到近心點的距離可以計算為
[到近心點的距離]
從主焦點到遠拱點的距離可以計算為
[遠拱點距離]
注意,這些方程是透過設定 θ = 0° 或 θ = 180° 得出的,因為近拱點位於零度,遠拱點位於 180 度。
活體方程
[edit | edit source]注意,在拱點處的速度必然垂直於位置向量,因此
可以推匯出以下表達式
回想一下特定機械能的表示式
將 rp、vp、ra 和 va 的值代入
關於 a 求解該方程得到
[活體方程]
軌道週期
[edit | edit source]軌道的週期可以表示為
[軌道週期]
請注意,該週期僅對橢圓軌道或圓形軌道有意義,因為拋物線和雙曲線永遠不會完成完整的旋轉。另請注意,該方程證明了開普勒第三定律。我們可以透過重新排列指數來看到這一點
現在很明顯,週期的平方與長半軸的立方成正比,長半軸是到太陽的平均距離。
圓形軌道週期與橢圓軌道週期類似,但圓形的軌道半徑為 *r*