生物經濟學

生物經濟學是關於對生物資源進行經濟開發的理論，它涉及兩個動態系統：種群動態和經濟系統的動態。因此，生物經濟學依託於兩個傳統的大學學科，生物學和經濟學。

生產理論簡要參考

生產理論是微觀經濟學的核心要素，簡單地描述了將投入（v）轉換為產出（Q）的過程

Q=Q({v_{1}},{v_{2}}....{v_{n}})\,\!

(2.1)

有多種方法可以指定此函式。一種是作為加法生產函式

Q={p_{0}}+{p_{1}}{v_{1}}+{p_{2}}{v_{2}}+...+{p_{n}}{v_{n}}\,\!

(2.2)

其中p₀、p₁、.... p_n是透過經驗確定的引數。

另一種是作為科布-道格拉斯生產函式（乘法）

Q={p_{0}}\cdot {v_{1}}^{p_{1}}\cdot {v_{2}}^{p_{2}}\cdot ...\cdot {v_{n}}^{p_{n}}

(2.3)

其他形式包括恆定彈性替代生產函式（CES），這是一個更通用的公式，包括科布-道格拉斯函式，以及二次生產函式，它是加法函式的一種特定型別。要使用的最佳方程形式以及引數的值因公司而異，也因行業而異。

在短期生產函式中，至少有一個（投入）是固定的。在長期中，原則上，所有要素投入都是可變的，由管理層自行決定。

在經典理論中，生產可能涉及三種類型的投入：勞動力 (L)、資本 (K) 和自然資源 (R)。一些經典著作將後者分為兩種：自然資源和能源 (E)。更常見的是，來自其他生產過程的產出被用作其他過程的投入。但原則上，應該有可能將所有投入分解為三種或四種基本型別。

短期捕撈產量

最簡單的捕撈產量模型只涉及兩個投入要素：一種自然資源 (x) 和一項捕撈活動（捕撈努力量，F）。

捕撈努力量的生產

讓我們開始討論一定數量的捕撈努力量的生產。此外，我們假設人力投入（可以被視為一種自然資源，但更實際的描述是勞動力）和資本（船舶、漁具等）是捕撈努力量生產中的兩種基本型別投入。還假設這兩種要素中的任何一種都可以被另一種要素以一定的數量完美替代。

F=F(L,K)\,\!

(3.1)

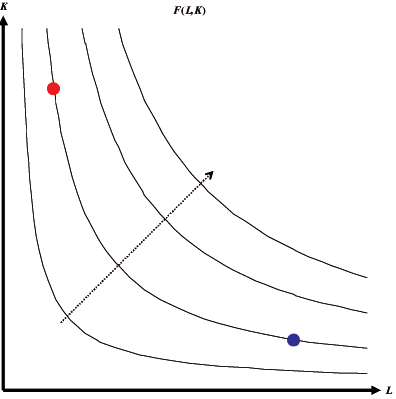
在將投入要素限制為兩種的情況下，替代率可以在等產量線圖中輕鬆檢視，通常稱為生產等產量線（圖 3.1）。

圖 3.1
捕撈努力量生產等產量線。
曲線顯示L（勞動力）可以以何種速度被K（資本）替代，反之亦然，每條曲線代表F的恆定產出。藍色點代表著一定量的捕撈努力量，其中涉及大量的勞動力投入，而紅色點中大部分的勞動力被資本替代，例如小船和手線（藍色點）與幾艘拖網漁船（紅色點）之間的區別。虛線箭頭表示努力量生產的增加。

有效生產的概念

公式 3.1 只是對生產要素 L 和 K 如何產生 F 的技術描述，並沒有給出關於哪種生產要素組合更優的建議。為了優先考慮生產特定數量 F 的不同方案，觀察兩種生產要素的成本會更方便。設勞動力 (L) 的單位成本為 w，資本 (K) 的單位成本為 r，則總生產成本 (C) 為：

C=wL+rK\,\!

(3.2)

可以使用拉格朗日方法在成本約束下最大化捕撈努力量的生產，這是在給定產量下最小化成本的對偶問題。拉格朗日方程為：

{\mathcal {L}}=F(L,K)-\lambda ({C_{0}}-wL-rK)

(3.3)

其中 C₀ 為給定的成本， $\lambda$ 為拉格朗日乘子。

最大化拉格朗日方程的一階條件是方程對 L 和 K 的偏導數等於 0，由此可得：

{\frac {\frac {\partial F}{\partial L}}{\frac {\partial F}{\partial K}}}={\frac {w}{r}}

(3.4)

這個表示式被稱為技術替代邊際率 (MRTS)。根據公式 (3.4)，在最具成本效益的生產中，MRTS 應該等於兩種生產要素的價格比率。圖 3.2 展示了不同生產水平的成本效益解決方案。

圖 3.2
高效生產。
粗線連線了當成本約束 C₀ 變化時，與公式 (3.4) 一致的無限多個點。

用兩種生產要素生產魚獲量。

透過將捕撈努力量的生產視為一個獨立的生產過程，(h，魚獲量) 的生產可以用兩個生產要素 x 和 F 來表示。

h=h(x,F)\,\!

(3.5)

可以合理地假設 x 和 F 與圖 3.1 中的 L 和 K 具有相同的可替代性。為了捕撈一定數量的魚，例如 1 公斤，當種群生物量較低 (x 值較低) 時，需要投入的捕撈努力量要比種群密度較高 (x 值較高) 的情況更大。

因此，公式 (3.5) 與公式 (3.1) 屬於同類，原則上我們具有與圖 3.1 中所示相同的連續替代型別。

使用共同資源時的市場失靈

然而，有兩個核心問題使這種生產成為一項截然不同的任務。

確定高效的生產水平需要來自完美市場的生產要素價格。在這種情況下，我們當然可以根據上面的段落計算出捕撈努力量 (F) 的完美市場價格。但另一個生產要素 x 的價格是多少？
如果該資源被視為公有財產，則價格將為零！在這種情況下，對我們想要用免費的生產要素 x 代替多少 F (F 具有正價格) 沒有限制，直到該資源被完全生產並轉化為魚獲量。
x 的可用性 (以及可及性) 在短期內是給定的。從長遠來看，它也將是給定的，現在是過去捕撈產量的函式。換句話說，這兩個生產要素相互關聯！由此，生產理論中的傳統方法失效。

第一個問題使我們無法繼續沿用識別成本效益解決方案的常規方法。由於自然資源的稀缺性沒有反映在價格中，我們缺乏關於該要素的價值資訊。另一個問題也損害了我們的模型，因為它攻擊了兩種生產要素可用性獨立性的基本假設。實際上，從長遠來看，我們有：