C++ 程式設計

變數

就像一個人擁有一個與其他人區分開的姓名一樣，變數為一個特定物件型別例項分配一個名稱或標籤，透過該名稱或標籤可以引用該例項。變數是程式設計中最重要的概念，它是程式碼如何操作資料的核心。根據其在程式碼中的用途，變數在硬體方面具有特定的區域性性，並且根據程式碼的結構，它還具有特定的作用域，在該作用域中，編譯器會將其識別為有效的。所有這些特性都是由程式設計師定義的。

內部儲存

我們需要一種方法來儲存資料，這些資料可以透過程式設計在硬體上儲存、訪問和修改。大多數計算機系統使用二進位制邏輯執行。計算機使用兩個電壓電平表示值，通常 0V 表示邏輯 0，+3.3 V 或 +5V 表示邏輯 1。這兩個電壓電平恰好代表兩個不同的值，按照慣例，這些值分別是零和一。這兩個值巧合地對應於二進位制數系統中使用的兩個數字。由於計算機使用的邏輯電平和二進位制數系統中使用的兩個數字之間存在對應關係，因此計算機採用二進位制系統就不足為奇了。

二進位制數系統

二進位制數系統使用以 2 為基數，因此只需要0 和1 兩個數字。

位和位元組

我們通常將二進位制數寫成一位序列（位是二進位制數字的簡稱）。這也是一個正常約定，這些位序列為了使二進位制數更易於閱讀和理解，在特定的相關邊界處新增空格，這些邊界將從使用該數字的上下文中選擇。就像我們在較大的十進位制數字中使用逗號（英國和大多數前殖民地）或點來隔開每三個數字一樣。例如，二進位制值 44978 可以寫成1010 1111 1011 0010。

這些是特定位序列的定義邊界。

名稱	大小（位）	示例
位	1	1
位元組	4	0101
位元組	8	0000 0101
字	16	0000 0000 0000 0101
雙字	32	0000 0000 0000 0000 0000 0000 0000 0101

位

二進位制計算機上最小的資料單位是一個位。由於單個位只能表示兩個不同的值（通常是零或一），你可能認為可以用單個位表示的專案數量非常少。不正確！你可以用一個位表示無數個專案。

用一個位，你可以表示任何兩個不同的專案。例如，零或一，真或假，開或關，男或女，對或錯。但是，使用多個位，你將不再侷限於表示二進位制資料型別（即只有兩個不同值的那些物件）。

更令人困惑的是，不同的位可以表示不同的東西。例如，一個位可能用於表示值零和一，而相鄰的位可能用於表示顏色紅色或黑色。你如何透過檢視位來判斷？答案當然是不行。但這說明了計算機資料結構的整個理念：資料就是你定義的。

如果你使用一個位來表示一個布林值（真/假），那麼該位（根據你的定義）就代表真或假。為了使該位具有任何真實意義，你必須保持一致。也就是說，如果你在程式中的某個地方使用一個位來表示真或假，你不應該在稍後使用該位中儲存的真/假值來表示紅色或黑色。

由於你將嘗試建模的大多數專案都需要超過兩個不同的值，因此單個位值並不是最流行的資料型別。但是，由於其他所有事物都由位組構成，因此位將在你的程式中發揮重要作用。當然，有一些資料型別需要兩個不同的值，因此似乎位本身很重要。但是，你很快就會看到，單個位很難操作，因此我們通常使用其他資料型別來表示布林值。

位元組

位元組是 4 位邊界上的位集合。除了兩個專案之外，它不會是一個特別有趣的資料結構：BCD（二進位制編碼十進位制）數字和十六進位制（16 進位制）數字。表示一個 BCD 或十六進位制數字需要四個位。

用一個位元組，我們可以表示多達 16 個不同的值。在十六進位制數字的情況下，值 0、1、2、3、4、5、6、7、8、9、A、B、C、D、E 和 F 用四個位表示。

BCD 使用十個不同的數字（0、1、2、3、4、5、6、7、8、9）並且需要四個位。實際上，任何 16 個不同的值都可以用一個位元組表示，但十六進位制和 BCD 數字是我們可以用一個位元組表示的主要專案。

位元組

位元組是我們可以在計算機上訪問或修改的最小單個數據塊，毫無疑問，它是當今微處理器使用最重要的資料結構。PC 中的主記憶體和 I/O 地址都是位元組地址。

在幾乎所有型別的計算機上，一個位元組都包含 8 位，儘管確實存在位元組更大的計算機。位元組是微處理器中最小的可定址資料（資料項），這就是為什麼處理器只能處理位元組或位元組組，而不能處理位的原因。要訪問任何更小的東西，你需要讀取包含資料的位元組並遮蔽掉不需要的位。

由於計算機是位元組可定址的機器，事實證明，操作整個位元組比操作單個位或位元組更有效率。因此，大多數程式設計師使用整個位元組來表示需要不超過 256 個專案的那些資料型別，即使少於 8 位就足夠了。例如，我們通常將布林值真和假分別表示為 00000001 和 00000000。

可能一個位元組最重要的用途是儲存一個字元程式碼。在鍵盤上輸入的字元、顯示在螢幕上的字元以及列印在印表機上的字元都具有數值。

一個位元組包含 8 位

一個位元組（通常）包含 8 位。一個位只能取 0 或 1 的值。如果所有位都設定為 1，則二進位制中的 11111111 等於十進位制中的 255。

一個位元組中的位從位零（b0）到七（b7）編號如下：b7 b6 b5 b4 b3 b2 b1 b0

位 0（b0）是低位或最低有效位（lsb），位 7 是高位或最高有效位（msb）。我們將透過它們的數字來引用所有其他位。

一個位元組也正好包含兩個位元組。位 b0 到 b3 構成低位位元組，位 b4 到 b7 構成高位位元組。

由於一個位元組包含 8 位，正好是兩個位元組，因此位元組值需要兩位十六進位制數字。它可以表示 2^8 或 256 個不同的值。一般來說，我們將使用一個位元組來表示

1. 範圍為 0 => 255 的無符號數值
2. 範圍為 -128 => +127 的有符號數
3. ASCII 字元程式碼
4. 其他需要不超過 256 個不同值的特殊資料型別。許多資料型別少於 256 個專案，因此 8 位通常就足夠了。

在本計算機位元組表示中，位號用於標記位元組中的每個位。位從 7 到 0 編號，而不是從 0 到 7 甚至從 1 到 8，因為處理器總是從 0 開始計數。正如我們將看到的那樣，對於計算機來說，使用 0 更加方便。位也按降序排列，因為與十進位制數字（正常的 10 進位制）一樣，我們將更重要的數字放在左側。

考慮十進位制中的數字 254。這裡的 2 比其他數字更重要，因為它表示百位，而不是 5 表示的十位或 4 表示的個位。二進位制也是如此。更重要的數字放在左邊。在二進位制中，只有 2 個數字，而不是從 0 計數到 9，我們只從 0 計數到 1，但計數的原理與十進位制計數完全相同。如果我們要計數超過 1，那麼我們需要在左邊新增一個更重要的數字。在十進位制中，當我們計數超過 9 時，我們需要在下一個重要的數字上加 1。有時它看起來可能令人困惑或不同，僅僅因為人類習慣於使用 10 個數字進行計數。

在十進位制中，每個數字代表 10 的冪的倍數。因此，在十進位制數 254 中。

• 4 代表四個 1 的倍數 ($4\times 10^{0}$ 因為 $10^{0}=1$）。
• 由於我們在十進位制（以 10 為底）中工作，因此 5 代表五個 10 的倍數 ($5\times 10^{1}$)
• 最後，2 代表兩個 100 的倍數 ($2\times 10^{2}$)

所有這些都是基本知識。關鍵是要認識到，當我們在數字中從右到左移動時，數字的意義以 10 的倍數增加。當我們看到以下等式時，這應該是顯而易見的

$(2\times 10^{2})+(5\times 10^{1})+(4\times 10^{0})=254$

在二進位制中，每個數字只能是兩種可能性之一（0 或 1），因此當我們處理二進位制時，我們使用的是以 2 為底而不是以 10 為底。因此，要將二進位制數 1101 轉換為十進位制，我們可以使用以下以 10 為底的等式，這與上面的等式非常相似

$(1\times 2^{3})+(1\times 2^{2})+(0\times 2^{1})+(1\times 2^{0})=8+4+0+1=13$

一個位元組包含 8 位

要轉換數字，我們只需將位值 ($2^{n}$) 相加，其中 1 出現在的位置。讓我們再看看我們示例位元組，並嘗試找到它在十進位制中的值。

首先，我們看到位 #5 是 1，所以我們有 $2^{5}=32$ 作為我們的總計。接下來是位 #3，所以我們加 $2^{3}=8$。這給了我們 40。然後下一個是位 #2，所以 40 + 4 是 44。最後是位 #0，得到 44 + 1 = 45。所以這個二進位制數在十進位制中是 45。

如您所見，不同的位組合不可能給出相同的十進位制值。這裡有一個簡單的示例，展示了二進位制（以 2 為底）計數和十進位制（以 10 為底）計數之間的關係。

$00_{2}$ = $0_{10}$, $01_{2}$ = $1_{10}$, $10_{2}$ = $2_{10}$, $11_{2}$ = $3_{10}$

這些數字所在的進位制顯示在數字右邊的下標中。

進位位

順便說一下，如果你給 255 加 1 會怎樣？除非我們新增更多位，否則任何組合都無法表示 256。下一個值（如果我們可以有另一個數字）將是 256。因此我們的位元組將是這樣的。

但是這個 $9^{th}$ 位（位#8）並不存在。那麼它去哪裡了呢？準確地說，它實際上進入了進位位。進位位駐留在計算機的處理器中，有一個專用於進位運算（如這種情況）的內部位。因此，如果在位元組中儲存的 255 中加 1，結果將是 0，並且 CPU 中的進位位將被設定。當然，C++ 程式設計師永遠不會直接使用此位。您需要學習組合語言才能做到這一點。

位元組序

在檢查完單個位元組之後，現在該看看如何表示大於 255 的數字了。這是透過將位元組分組來實現的，我們可以表示比 255 大得多的數字。如果我們將 2 個位元組組合在一起，我們就會使數字中的位數加倍。實際上，16 位允許表示高達 65535 的數字 (unsigned)，而 32 位允許表示超過 40 億的數字。

3 種基本基本型別 char、short int、long int。

以下是一些基本的基本型別

• char (1 位元組（根據定義），最大 unsigned 值：至少 255)

• short int (至少 2 個位元組，最大 unsigned 值：至少 65535)

• long int (至少 4 個位元組，最大 unsigned 值：至少 4294967295)

• float (通常為 4 個位元組，浮點數)

• double (通常為 8 個位元組，浮點數)

關於位元組的所有資訊都適用於其他基本型別。區別僅僅在於使用的位數不同，而 msb 現在對於 short 而言是位#15，對於 long 而言是位#31（假設 32 位 long 型別）。

在 short（16 位）中，人們可能會認為在記憶體中，位 15 到 8 的位元組將緊隨位 7 到 0 的位元組。換句話說，位元組 #0 將是高位元組，而位元組 #1 將是低位元組。對於其他一些系統來說，這是正確的。例如，摩托羅拉 68000 系列 CPU 確實使用這種位元組順序。但是，在 PC 上（使用 8088/286/386/486/奔騰），情況並非如此。順序相反，因此低位元組位於高位元組之前。表示位 0 到 7 的位元組始終位於 PC 上所有其他位元組之前。這被稱為小端位元組序。其他順序（如 M68000 上的順序）稱為大端位元組序。在執行旨在跨系統移植的低階位元組操作時，這一點非常重要。

對於大端計算機，基本思想是將高位放在左邊或前面。對於小端計算機，基本思想是將低位放在低位元組中。除了一個奇特之處之外，這兩種方案沒有內在的優勢。使用小端 long int 作為更小的 int 型別在理論上是可行的，因為低位元組始終位於相同的位置（第一個位元組）。在大端中，低位元組的位置始終不同，具體取決於型別的尺寸。例如（在大端中），低位元組是 long int 中的第 $4^{th}$ 個位元組，而 short int 中的第 $2^{nd}$ 個位元組。因此，必須進行適當的型別轉換，低階技巧變得相當危險。

要從一種位元組序轉換為另一種位元組序，需要反轉位元組的值，將最高位元組的值放在最低位元組中，將最低位元組的值放在最高位元組中，並交換所有中間位元組的值，因此，如果有一個 4 位元組小端整數 0x0A0B0C0D（0x 表示值為十六進位制），那麼將其轉換為大端將把它更改為 0x0D0C0B0A。

位位元組序，其中位元組內部的位順序發生變化，很少用於資料儲存，而且實際上只有在序列通訊鏈路中才真正重要，在這些鏈路中，硬體處理它。

有一些計算機不遵循嚴格的大端或小端位佈局，但它們很少見。一個例子是 PDP-11 儲存 32 位值的方式。

瞭解二進位制補碼

補碼是一種在純二進位制表示中儲存負數的方法。選擇補碼方法來儲存負數的原因是，它允許 CPU 對有符號和無符號數字使用相同的加減指令。

要將一個正數轉換為其負補碼格式，您首先要翻轉該數中的所有位（1 變成 0，0 變成 1），然後加 1。（這也能將負數轉換回正數，例如：-34 轉換為 34，反之亦然）。

一個位元組包含 8 位

讓我們嘗試將數字 45 轉換為補碼。

一個位元組包含 8 位

首先，我們將所有位翻轉...

一個位元組包含 8 位

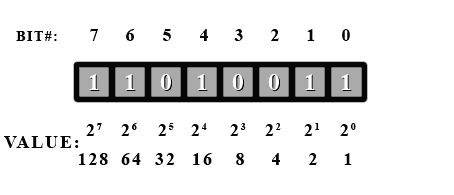
然後加 1。

現在，如果我們將所有 1 位的值加起來，我們得到... 128+64+16+2+1=211？這裡發生了什麼？嗯，這個數字實際上是 211。這完全取決於你如何解釋它。如果你認為這個數字是無符號，那麼它的值是 211。但如果你認為它是帶符號的，那麼它的值是 -45。你完全可以自己決定如何處理這個數字。

當且僅當你決定將它視為一個帶符號的數字時，請檢視 msb（最高有效位 [位#7]）。如果它是 1，那麼它是一個負數。 如果它是 0，那麼它是一個正數。在 C++ 中，在型別前面使用無符號將告訴編譯器你希望將此變數用作無符號數字，否則它將被視為帶符號數字。

現在，如果你看到 msb 被設定了，那麼你就會知道它是負數。所以使用上面描述的步驟將其轉換回正數以找出它的實際值。

讓我們看幾個例子。

將以下數字視為一個無符號位元組。它的十進位制值是多少？

一個位元組包含 8 位

由於這是一個無符號數字，不需要特殊處理。只需將所有 1 位的值加起來。128+64+32+4=228。所以這個二進位制數字在十進位制中是 228。

現在將上面的數字視為一個帶符號的位元組。它的十進位制值是多少？

由於現在是一個帶符號的數字，我們首先要檢查 msb 是否被設定。讓我們看看。是的，位#7 被設定了。所以我們必須進行補碼轉換才能將其值作為正數獲取（然後我們在後面新增負號）。

一個位元組包含 8 位

好的，所以讓我們翻轉所有位...

一個位元組包含 8 位

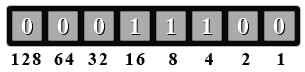
然後加 1。這有點棘手，因為進位會傳播到第三位。對於位#0，我們執行 1+1 = 10（二進位制）。所以位#0 有一個 0。現在我們必須將進位加到第二位（位#1）。1+1=10。位#1 是 0，我們再次將 1 進位到$3^{rd}$ 位（位#2）。0+1 = 1，我們完成了轉換。

現在，我們將所有 1 位的值加起來。16+8+4 = 28。由於我們進行了轉換，因此我們將負號加起來得到 -28 的值。所以，如果我們將 11100100（二進位制）視為一個帶符號的數字，它的值是 -28。如果我們將其視為一個無符號數字，它的值是 228。

讓我們嘗試最後一個例子。

給出以下二進位制數字的十進位制值，既作為帶符號數，也作為無符號數字。

一個位元組包含 8 位

首先作為無符號數字。所以我們將所有 1 位的值加起來。4+1 = 5。對於無符號數字，它的值是 5。

現在對於帶符號的數字。我們檢查 msb 是否被設定。不，位#7 是 0。所以對於帶符號的數字，它的值也是 5。

如你所見，如果帶符號的數字的 msb 沒有被設定，那麼你將它完全視為無符號數字。

浮點數表示

具有小數部分的通用實數也可以用二進位制格式表示。例如，二進位制中的 110.01 對應於

$1\times 2^{2}+1\times 2^{1}+0\times 2^{0}+0\times 2^{-1}+1\times 2^{-2}={\color {Blue}2^{2}+2^{1}+2^{-2}}=6.25$

指數表示法（也稱為科學記數法或標準形式，當與基數 10 一起使用時，如$3\times 10^{8}$) 也可以使用，同一個數字可以表示為

$1.1001\times 2^{2}\qquad (=11.001\times 2^{1}=110.01)$

當小數點左側只有一個非零數字時，該表示法被稱為規範化。

在計算應用中，實數由符號位 (S)、指數 (e) 和尾數 (M) 表示。指數域需要表示正負指數。為此，將偏置 E 新增到實際指數以獲得儲存的指數，並將符號位 (S)（指示數字是否為負）轉換為 +1 或 -1，得到 s。因此，實數表示為

$f=s\times M\times 2^{e-E}$

S、e 和 M 在一個 32 位字中一個接一個地連線起來以建立一個單精度浮點數，在 64 位雙字中連線起來以建立一個雙精度浮點數。對於單精度浮點型，使用 8 位表示指數，使用 23 位表示尾數，指數偏移量為 E=127。對於雙精度浮點型，使用 11 位表示指數，使用 52 位表示尾數，指數偏移量為 E=1023。

浮點數有兩種型別：規格化和非規格化。規格化數的指數 e 在 0<e<2⁸ - 1（在 00000000 和 11111111 之間，不包括）範圍內，對於單精度浮點數，指數 e 在 0<e<2¹¹ - 1（在 00000000000 和 11111111111 之間，不包括）範圍內，對於雙精度浮點數。規格化數表示為符號乘以 1.尾數乘以 2^e-E。非規格化數是指指數為 0 的數字。它們表示為符號乘以 0.尾數乘以 2^1-E。非規格化數用於儲存值為 0 的值，其中指數和尾數均為 0。浮點數可以儲存 +0 和 -0，具體取決於符號。當數字不是規格化或非規格化時（其指數全為 1），如果尾數為零，則數字將為正無窮或負無窮，具體取決於符號；如果尾數不為零，則數字將為正 NaN（非數字）或負 NaN（非數字），具體取決於符號。

例如，數字 5.0（使用 float 型別）的二進位制表示為

0 10000001 01000000000000000000000

第一個位是 0，表示數字為正，指數為 129-127=2，尾數為 1.01（注意，前導 1 不包括在二進位制表示中）。1.01 在十進位制表示中對應於 1.25。因此 1.25*4=5。

浮點數並不總是值的精確表示。像 1010110110001110101001101 這樣的數字無法用單精度浮點數表示，因為，不考慮前導 1（不是尾數的一部分），有 24 位，而單精度浮點數只能在其尾數中儲存 23 個數字，所以最後的 1 必須丟棄，因為它是最不重要的位。此外，有些值在十進位制中可以很容易地表示，但在二進位制中卻無法表示，例如，十進位制中的 0.3 將是 0.0010011001100110011... 或者類似的東西。許多其他數字無法用二進位制浮點數精確表示，無論其尾數使用多少位，僅僅因為它會產生像這樣的重複模式。

區域性性（硬體）

變數具有兩個不同的特徵：在堆疊上建立的變數（區域性變數）和透過硬編碼記憶體地址訪問的變數（全域性變數）。

全域性變數

通常，一個變數繫結到 計算機記憶體 中的特定地址，該地址在執行時自動分配，其固定位元組數由變數的物件型別的尺寸和對變數執行的任何操作決定，並影響儲存在該特定記憶體位置中的一個或多個 值。

所有全域性定義的變數都將具有靜態生命週期。只有那些未定義為 const 的變數預設情況下允許外部連結。

區域性變數

如果變數的大小和位置事先未知，則該變數在記憶體中的位置儲存在另一個變數中，而原始變數的大小由儲存第一個變數記憶體位置的第二個值的型別的尺寸決定。這被稱為 引用，而儲存其他變數記憶體位置的變數稱為指標。

範圍

變數也駐留在特定的 範圍 中。變數的範圍是決定變數生命週期的最重要的因素。進入範圍開始變數的生命週期，離開範圍結束變數的生命週期。當在範圍內時，變數是可見的，除非它被封閉範圍內具有相同名稱的變數隱藏。變數可以位於全域性範圍、名稱空間 範圍、檔案範圍或複合語句範圍。

例如，在以下程式碼片段中，變數 'i' 僅在相應的註釋之間的行中處於範圍內

{
  int i; /*'i' is now in scope */
  i = 5;
  i = i + 1;
  cout << i;
}/* 'i' is now no longer in scope */

有一些特定的關鍵字可以延長變數的生命週期，而複合語句定義自己的區域性 範圍。

// Example of a compound statement defining a local scope
{

  {
    int i = 10; //inside a statement block
  }

 i = 2; //error, variable does not exist outside of the above compound statement 
}

在同一級別的範圍內宣告同一個變數兩次是錯誤的。

全域性變數唯一可以定義的 範圍 是 名稱空間，它處理變數的可見性，而不是其有效性，其主要目的是避免名稱衝突。

在處理類時，與變數相關的範圍的概念變得極其重要，因為建構函式在進入範圍時被呼叫，而解構函式在離開範圍時被呼叫。