CLEP 代數/函式

在數學中，描述某一操作中輸入集如何表示該操作的輸出，往往至關重要。數學為此而創造的工具叫做函式。函式的正式定義可能是一個很難完全理解的障礙，而理解它的最好方法可能是使用直觀的概念進行實踐（作為目標的初步步驟，即理解）。因此，我們將從本章開始，對這種“處理”過程提供一個直觀的理解。

函式的直觀應用和定義

您可以將函式想象成一種機器。您將原材料（作為輸入）投入機器，機器將原材料轉化成成品（輸出）。讓我們用廚師來描述一個函式。將一片生菜交給廚師，他就會將它切碎，輸出就是切碎的生菜。數學中的函式有點類似。這種觀點足以讓我們至少了解它的實際應用。

示例 1.1(a)：日常生活中的函式 1 想象一下從橋上掉下一個球。在每時每刻，球都有一定的速度，$\mathbf {v}$。球的速度是時間的函式。這種函式被稱為實值函式，因為“成品”是一個數字（更準確地說，是一個實數）。

示例 1.1(b)：日常生活中的函式 2 想象一下，一條河流的平均水溫每天變化$4^{\circ }{\text{ F}}$。如果每天對河流進行水溫取樣，每天取樣$n=30$次，所有樣本的總體平均值為$\mu$，而偏差$\sigma =4^{\circ }{\text{ F}}$，那麼我們可以使用以下的正態（或“高斯”）函式來反映河流水溫的分佈 $\varphi (x)={\frac {1}{\sigma {\sqrt {2\pi }}}}e^{-{\frac {1}{2}}\left({\frac {x-\mu }{\sigma }}\right)^{2}}$ 如果相反，這條河只偏離平均水溫$4^{\circ }{\text{ F}}$，那麼可以用絕對值來表示 $|x-\mu |=4=T(x)$ 無論哪種方式，函式在日常生活中都有應用。

將實值函式想象成一個輸入-輸出機器；您將輸入交給函式，它會給您一個輸出，這個輸出是一個數字（更準確地說，是一個實數）。例如，平方函式接受輸入$4$，並給出輸出值$16$。相同的平方函式接受輸入$-1$，並給出輸出值$1$。

人們描述函式的方式有很多種。在第一個例子中，給出了一個口頭描述（球在地球上方的高度是時間的函式）。在第二個例子中，給出了某些函式的不同操作。下面將具體介紹使用操作來描述函式的方法

1. 函式被賦予一個名稱（例如 $f$），同時也會給出函式的公式。例如，$f(x)=3x+2$ 描述了一個函式。我們將輸入稱為函式的引數（或自變數），將輸出稱為函式在給定引數時的值。（注意：下一節將詳細介紹此記號。）
2. 函式使用方程式和兩個變數來描述。一個變數用於函式的輸入，另一個用於函式的輸出。輸入的變數稱為自變數。輸出的變數稱為因變數。例如，$y=3x+2$ 描述了一個函式。因變數單獨出現在等號的左側。

當函式被賦予一個名稱（如上面數字 1 中所示）時，函式的名稱通常是字母表中的單個字母（例如 $f$ 或 $g$）。一些函式具有多個字母的名稱（如正弦函式 $y=\sin(x)$。

讓我們透過再次回顧第一個示例來練習使用上面描述的第二種方法分配函式。

示例 1.1(c)：球的速度作為高度的函式 想象一下，作為一名物理學家，你被要求描述速度作為高度的函式。以下是可能最適合描述的內容（使用能量方程） 在時間 $t=0$ 時，球的位置處於最大高度 $h=H>0$。 在時間 $t=T$（撞擊時間）時，球處於最小高度 $h=0$（假設）。 在兩者之間，球的速度正在發生變化。假設初始水平速度和垂直速度分別為 $v_{0x}=0$ 和 $v_{0y}=0$（這是因為我們丟下了球）。水平速度不會改變（假設沒有空氣阻力），但垂直速度會降低。因此，最終的垂直速度為 $v_{y}<0$。因此，我們只需要關注垂直速度。 以上資訊使我們能夠將球的速度近似為高度的函式。 $\mathbf {v} (h)=-{\sqrt {2gh}}$，其中 $g=9.81{\frac {\text{m}}{{\text{s}}^{2}}}$。

以上等式是稱為複合函式的特殊型別函式的示例。此函式將在後面詳細解釋。現在，只需要直覺。

希望學生已經開始形成直覺。現在讓我們看看如何在某些輸入處評估函式。

示例 1.1(d)：給定輸出的輸入是什麼？（第 1 部分） 如果我們寫 $f(x)=3x+2$，那麼我們知道 $f$ 是 $x$ 的函式。 要評估某個數字的函式，只需用該數字替換 $x$。 用右側函式中的那個數字替換 $x$ 將會得到該特定輸入的函式輸出。 用英語來說，$f$ 的定義解釋為“給定一個數字，$f$ 將會返回輸入的三倍加二。” 基於以上要點，在某一點上評估函式的方法是 ${\begin{aligned}f(3)&=3\cdot (3)+2\\&=9+2\\&=11\end{aligned}}$ 因此，$f(3)$ 的值是 $f(3)=11$。當我們輸入3 時，$f$ 在 3 處的值為 11。 請注意，$f(3)$ 表示當$x$（自變數）取值為 3 時，因變數的值。因此，我們看到，當我們輸入3 時，函式的輸出為11。人們經常用“3 時，$f$ 的值為 11” 或者簡單地“$f$ 的 3 等於 11” 來總結以上工作。

示例 1.1(e)：給定輸出的輸入是什麼？(第 2 部分) 讓我們回到我們在示例 1.1(c) 中推匯出的函式。對於函式 $\mathbf {v} (h)=-{\sqrt {2gh}}$，其中 $g=9.81{\frac {\text{m}}{{\text{s}}^{2}}}$，我們知道以下內容是正確的 速度 $\mathbf {v}$ 是高度 $h$ 的函式。 用英語來說，$\mathbf {v}$ 的定義解釋為“給定地面上方的某個高度，$\mathbf {v}$ 將會根據兩次重力常數與高度的乘積的平方根返回球的速度。” 在處理現實生活中應用中的函式時，重要的是要記住單位。由於使用國際單位制，重力常數 $g$ 的單位是米每二次方秒，因此高度將以米為單位。我們想要知道如果球處於橋和地面之間一半的位置，$h={\frac {H}{2}}$，速度是多少。假設 $H=9.0{\text{ m}}$。讓我們開始評估函式 ${\begin{aligned}\mathbf {v} \left({\frac {9}{2}}\right)&=-{\sqrt {2g\left({\frac {9.0}{2}}\right)}}\\&=-{\sqrt {g\cdot 9.0}}\\&=-3.0{\sqrt {9.81}}\approx -9.4{\frac {\text{m}}{\text{s}}}\end{aligned}}$ 因此，$\mathbf {v} (4.5)$ 的值為 $\mathbf {v} (4.5)\approx -9.4{\frac {\text{m}}{\text{s}}}$。$\mathbf {v}$ 在 $4.5$ 處的值為 $-9.4{\frac {\text{m}}{\text{s}}}$。與 $0$ 米每秒相比，速度有了很大的提高！

關於符號的說明

函式使用非常廣泛，因此有專門的符號來表示它們。這種符號有些含糊，因此熟悉它對於理解方程式或公式的意圖很重要。

雖然對函式命名沒有嚴格的規則，但使用字母 $f$，$g$ 和 $h$ 來表示函式，使用變數 $x$ 來表示自變數。 $y$ 用於表示因變數和自變數。

當討論或使用函式 $f$ 時，重要的是不僅要了解函式本身，還要了解其自變數 $x$ 。因此，當提到函式 $f$ 時，通常不寫 $f$ ，而是寫 $f(x)$ 。現在，這個函式被稱為“$f$ 的 $x$”。函式名與自變數（在括號內）相鄰。這對於指示函式在自變數特定值時的值非常有用。例如，如果

$f(x)=7x+1$,

並且如果我們想使用 $f$ 的值，當 $x$ 等於 $2$ 時，我們將在上面定義的兩邊用 $2$ 代替 $x$ ，並寫

$f(2)=7(2)+1=14+1=15$

這種表示法比省略自變數，只寫 $f$ 更具資訊量，但可能存在歧義，因為 $f$ 旁邊的括號可能會被誤解為乘法，$2f$ 。為了確保沒有人意外地對錶示法感到困惑，請遵循以下步驟

1. 透過將函式 $f$ 等於某個表示式來定義它。
2. 給出類似以下的句子：“在 $x=c$ 時，函式 $f$ 為...”。
3. 計算函式的值。

如果學生正在參加選擇題考試，那麼這個步驟可能會改變，因為在這種情況下，交流並不重要。

將直覺形式化

截至目前，下面的定義可能不太容易理解。請閱讀定義，以便你能理解對映的概念。

函式

將一個集合（稱為**定義域**，$A$）中的元素對映到另一個集合（稱為值域，$B$）中的元素的對映，就是一個函式。對於從函式定義域中選擇的每個值，在函式值域中都存在恰好一個相應的元素。

現在，分析一下定義。注意，值域中的元素是透過從定義域對映元素的對應關係找到的。下面給出了一個例子。

令函式 $f(x)=5x+{\frac {5x}{2}}$ 對所有 $x$ 都成立。當 $x$ 等於多少時，$f(x)=225{\frac {1}{2}}$？ 在數學中，重要的是要注意任何重複。如果某些內容似乎重複，請把它記在腦海中。 在這裡，注意到 $f(x)=5x+{\frac {5x}{2}}$ 和 $f(x)=225{\frac {1}{2}}$。因為 $f(x)$ 等於兩個不同的值，因此等號另一邊的值必須相等。這種性質稱為傳遞性質（永遠記住實數的性質） $225{\frac {1}{2}}=5x+{\frac {5x}{2}}$ 接下來，簡化——讓你的生活更輕鬆，而不是更難。在這種情況下，由於 $5x+{\frac {5x}{2}}$ 有 $x$ 作為同類項，這兩個項是加在一起的，並且是分數，所以把它放在一個共同的分母上並簡化。類似地，由於 $225{\frac {1}{2}}$ 是一個帶分數，所以 $225{\frac {1}{2}}=225+{\frac {1}{2}}$. $225{\frac {1}{2}}=5x+{\frac {5x}{2}}$ $\Rightarrow {\frac {225}{1}}+{\frac {1}{2}}={\frac {5x}{1}}+{\frac {5x}{2}}$ $\Rightarrow {\frac {450}{2}}+{\frac {1}{2}}={\frac {10x}{2}}+{\frac {5x}{2}}$ $\Rightarrow {\frac {451}{2}}={\frac {15x}{2}}$ 將等式兩邊乘以 $x$ 係數的倒數，即 ${\frac {2}{15}}$。 ${\frac {2}{15}}\cdot {\frac {451}{2}}=x$ ${\frac {451}{15}}=x$ 或 $x={\frac {451}{15}}$. 使 $f(x)=225{\frac {1}{2}}$ 的 $x$ 值為 $x={\frac {451}{15}}$.$\blacksquare$.

在傳統上，從定義域中“選取”的元素被描繪成被輸入函式的東西（輸入），而範圍中相應的元素被描繪成輸出。注意這裡語言的特殊性：一個輸入是從定義域中選取的，這意味著定義域是所有輸入的集合；一個輸出是由那個特定的輸入產生的，這意味著範圍是所有可能的輸出的集合。

由於我們“選取”定義域中與我們想要查詢的範圍元素相對應的元素，因此我們可以控制選擇哪個元素，因此該元素也被稱為“自變數”。範圍中的元素不受我們控制，並由函式“對映”到。因此，該元素也被稱為“因變數”，因為它取決於我們選擇的自變數。由於它是一個元素，所以輸入也被稱為自變數。類似地，輸出也被稱為因變數。

函式的概念一開始更容易理解（對於大多數學生來說）。然而，函式的正式定義對於我們所知道的代數基礎的重要性意味著應該高度重視函式的正式定義。然而，這並不意味著直覺是不必要的甚至有害的。相反，學生應該能夠理解這兩種觀點，並能夠將它們聯絡起來。因此，我們認為學生應該堅持這兩種觀點。

回顧一下，函式 $f$ 是將某個元素 $x\in A$（稱為定義域）對映到唯一一個元素 $y\in B$（稱為值域），使得 $f:A\to B$。下面的影像有助於解釋函式的現代定義。

集合 $A$（定義域）將每個元素 $a$ 對映到集合 $B$ 中與其對應的元素 $b$。

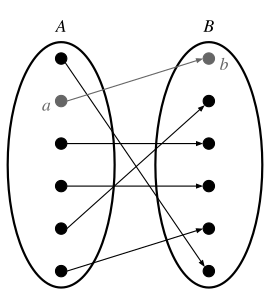
函式的基礎：對映、笛卡爾積和有序對

現在我們理解了集合，我們將開始理解函式的基本屬性（對映）。然而，元素是如何“對映”到另一個集合的？當組合“繫結”到另一個元素時，就會發生這種對映。在沒有集合的幫助下，定義“繫結”將很困難。然而，集合很好地定義了繫結，它是透過有序對來實現的。

透過庫拉托夫斯基形式化的有序對

一個有序對被定義為以 $(a,b)$ 形式書寫的集合，即

$(a,b){\overset {\underset {\mathrm {def} }{}}{=}}\left\{\left\{a\right\},\,\left\{a,b\right\}\right\}$.

這裡的邏輯是，包含在內的集合是一個依賴於書寫對順序的元素。因為 $\{a,b\}$ 使用了兩個元素，這個集合根據書寫對的順序給出第二座標。然而，這個定義對於 $b=a$ 不適用，因為它會得到 $(a,a)=\left\{a\right\}$，這不能準確地反映第二座標。但是，這個定義對於本教科書的目的來說已經足夠好了。此外，本文所述的知識通常不會在大學代數課程中教授。

笛卡爾積

設 $A$ 和 $B$ 是兩個不同的集合。如果我們要將這兩個集合合併，它將被定義為笛卡爾積 $A\times B$ （讀作 $A$ 叉乘 $B$）。 $A\times B$ 是所有有序對 $(x,y)$ 的集合，其中 $x\in A$ 且 $y\in B$

$A\times B=\left\{(x,y)|x\in A\wedge y\in B\right\}$ （讀作 $A$ 叉乘 $B$ 是包含有序對 $x,y$ 的集合，使得 $x$ 屬於 $A$ 且 $y$ 屬於 $B$。 楔形符號 $\wedge$ 是邏輯符號，表示“且”)。

笛卡爾積的本質希望不言而喻。當兩個集合以這種方式合併時，就會產生有序對。這與函式的定義非常接近。畢竟，這個積的子集就是函式（在大多數情況下）。

對映

設 $A$ 和 $B$ 是兩個不同的集合。一個 **從 $A$ 到 $B$ 的 **對映 $f$** 是一個關係，使得笛卡爾積 $A\times B$ 的子集 $S$ 在以下條件下導致 $f=(A,B,S)$

• 對於所有 $x\in A$ 和 對於所有 $y_{1},y_{2}\in B$,
• 有序對 $(x,y_{1})$ 和 $(x,y_{2})$ 都在子集 $S$ 中
• 暗示 $y_{1}=y_{2}$, 並且
• 對於所有 $x\in A$，存在一個 $y\in B$ 使得 $(x,y)\in S$.

符號 $f:A\to B$ 或 $A\xrightarrow {f} B$ 是對定義的簡潔表示（大聲讀出來是 $f$ 將 $A$ 對映到 $B$）。

上述所有定義的意思是，給定稱為定義域和值域的集合的笛卡爾積，存在一個有序對 $(x,y)$ 的關係，將定義域與值域聯絡起來。對於本書而言，首選第一個符號 ($f:A\to B$)。

使用集合查詢函式的新屬性

從上面的定義中，現在出現了一些新問題。以下列出三個主要問題：函式可以是（1）一對一嗎？（2）多對一嗎？（3）一對多嗎？考慮每種情況。

1. 如果函式 $f$ 的定義域 $A$ 中的一個元素 $a\in A$ 導致值域 $B$ 中的唯一元素 $b\in B$，則該函式被認為是 **一對一** 的。根據定義，由於只有一個元素 $b$ 由函式 $f$ 從某個元素 $a$ 對映，$f:A\to B$ 意味著存在來自對映的唯一元素 $b$。因此，存在一對一函式，因為它符合函式的定義。此定義類似於 *圖 1*。
2. 如果某些元素 $a_{1},a_{2},\ldots a_{n}\in A$ 來自函式 $f$ 的定義域 $A$ 對映到函式 $f$ 的值域 $B$ 中的恰好一個元素 $b\in B$，那麼該函式被稱為多對一函式。 由於某些元素 $\left(a_{1},a_{2},\ldots a_{n}\right)\in A$ 必須對映到恰好一個元素 $b\in B$，因此 $f:A\to B$ 必須符合函式的定義。 因此，存在多對一函式。
3. 如果函式 $f$ 的定義域 $A$ 中的恰好一個元素 $a\in A$ 對映到函式 $f$ 的值域 $B$ 中的某些元素 $\left(b_{1},b_{2},\ldots b_{n}\right)\in B$，那麼該函式被稱為一對多函式。 如果某個元素 $a$ 對映到多個不同的元素 $b$，那麼 $f:A\to B$ 不是函式，因為存在多個不同的元素 $b$。 由於多對一不符合函式的定義，因此不存在一對多函式。

現代的函式定義足夠完整，它可以幫助我們判斷一種新的“函式”型別是否真的是一個函式。 現在我們已經定義了每種情況，你可以證明一個函式屬於哪種函式型別。 以下是一個示例問題。

給定：$f(x)=ax+b$，其中$a$和$b$是常數，且$a\neq 0$。 證明：函式$f$是單射的。 注意函式$f$中唯一變化的元素是$x$。透過應用定義來證明函式是單射的可能是無法實現的，因為雖然定義域集合$A$中的兩個隨機元素可能不是一對多，但也可能存在一些元素$\left(a_{1},a_{2},\ldots a_{n}\right)\in A$使得函式成為一對多。為了解決這種可能性，我們必須證明不可能出現類似的結果。 假設存在兩個不同的元素$x_{1}$和$x_{2}$，它們會導致$f\left(x_{1}\right)=f\left(x_{2}\right)$。這將使函式成為一對多。因此， $$ax_{1}+b=ax_{2}+b$$ 從等式的兩邊減去$b$。 $\Rightarrow ax_{1}=ax_{2}$ 從等式的兩邊減去$ax_{2}$。 $\Rightarrow ax_{1}-ax_{2}=0$ 從等式左邊兩項中提取公因子$a$。 $\Rightarrow a\left(x_{1}-x_{2}\right)=0$ 在等式的兩邊乘以${\frac {1}{a}}$。 $\Rightarrow \left(x_{1}-x_{2}\right)=0$ 在等式兩邊加上 $x_{2}$。 $\Rightarrow x_{1}=x_{2}$ 注意 $x_{1}=x_{2}$。但是，這是不可能的，因為 $x_{1}$ 和 $x_{2}$ 是不同的。因此，$f\left(x_{1}\right)\neq f\left(x_{2}\right)$。兩個不同的輸入不能產生相同的輸出。因此，該函式必須是一一對應函式。

從函式的現代定義中可以學到一些更重要的概念，這些概念源於瞭解域、值域和陪域之間的區別。我們已經討論過其中一些概念，但是瞭解集合的概念為以下每個概念添加了新的定義。因此，讓我們根據這些新概念來討論這些概念。下面的定義有點令人困惑。解讀這些定義的最佳方法是畫圖。在這些定義的右側是與其對應的影像（包括相應定義的正式定義）。

元素 $a\in A$ 是一個輸入。整個集合 $A$ 是域（因為它包含所有輸入）。對於任何 $r\in B$ 但 $r\notin R$ 並且 $b\in R$ 給出 $R=\{b\}$，其中 $R$ 是 $B$ 的子集，這意味著 $R$ 是值域。集合 $B=\{R,c\}$ 是陪域。

• 定義域是指一個集合 $A$，其中所有元素 $a\in A$ 都對映到至少一個唯一的 $b\in B$。
• 集合 $B=R\cup \{r\}$ 和 $R=\{b\}$ 意味著 $R$ 是函式 $f$ 在笛卡爾積中的值域，其中所有元素 $a\in A$ 都對映到至少一個唯一的元素 $b\in B$。也就是說，值域是所有被某些 $a\in A$ 對映到對應 $b\in R$ 的元素的集合。
• 陪域是指集合 $B$，不一定所有元素 $b\in B$ 都被某些 $a\in A$ 對映到。也就是說，$B$ 中所有元素的集合就是陪域。

透過使用一個能夠將這些概念具體化的函式，可以使抽象概念更容易理解。假設有一個函式 $f$，其中 $x\neq 2$。令該函式為 $f(x)=2x-1$，其中 $y=f(x)$。讓我們寫下這個特定函式的定義域、值域和陪域。

• 域：$x\in (-\infty ,2)\cup (2,\infty )$ 或 $\left\{x|x\in \mathbb {R} \wedge x\neq 2\right\}$ 或簡化為 $x\neq 2$。在這種情況下，域是集合 $A$ 中除了 $x=2$ 之外的所有元素的集合，因為這個元素不能對映到集合 $B$ 中的任何元素。
• 值域：$y\in (-\infty ,3)\cup (3,\infty )$ 或 $\left\{y|y\in \mathbb {R} \wedge y\neq f(2)\right\}$ 或簡化為 $y\neq f(2)$。在這種情況下，值域是集合 $B$ 中除了 $y=f(2)$ 之外的所有元素的集合，因為這個元素不能被集合 $A$ 中的任何元素對映。
• 陪域：$y\in (-\infty ,\infty )$ 或 $\left\{y|y\in \mathbb {R} \right\}$ 或 $y\in \mathbb {R}$。這包括我們之前不允許對映的元素。

還需要定義最後一個方面。我們已經很好地瞭解了是什麼讓對映成為函式（例如，它不能是一對多）。但是，在討論以下內容時，還需要三個你經常聽到的定義：單射、滿射、雙射。

• 如果一個函式是一對一的，則該函式為單射。也就是說，對於 $a_{1}\in A$ 和 $a_{2}\in A$，如果 $f(a_{1})=f(a_{2})$，則 $a_{1}=a_{2}$。否則，它就不是一對一的。之前關於一對一的定義同樣適用於單射（意識到單射和一對一的定義是相同的）。
• 如果一個函式是滿射，它就是“到”的。也就是說，對映 $f:A\to B$ 的值域是 $B$，其中函式的陪域和值域是相同的。
• 如果一個函式既是滿射又是單射，它就是雙射。

以上定義經常讓人感到非常困惑。為了更好地理解，在專案符號旁邊提供了一張圖片，並提供了一個新的例子。讓我們分析函式 $g(x)=ax^{2}$。

已知：$g(x)=ax^{2}$，其中 $a$ 為常數且 $a\neq 0$。 證明：函式 $g$ 非滿射且非單射。 注意，函式 $g$ 中唯一變化的元素是 $x$。讓我們檢查一下這個函式的條件。 它是否單射？令 $g(x)=y$，並求解 $x$。首先，用 $a$ 除。 $y=ax^{2}$ $\Rightarrow {\frac {y}{a}}=x^{2}$ 然後對 $x^{2}$ 開平方根。根據定義，${\sqrt {x^{2}}}=\left\vert x\right\vert =\pm x$，所以 $\Rightarrow {\sqrt {\frac {y}{a}}}=\pm x$ 然而，請注意我們從上述操作中得出的結論。由於求解$x$，我們發現有兩個輸入，$\pm x$，產生相同的輸出，${\sqrt {\frac {y}{a}}}$。這意味著對於某個特定的$x$，它產生$y$，有兩個不同的輸入會導致相同的值。因為當$x_{1}\neq x_{2}$時，$f(x_{1})=f(x_{2})$，根據定義，它不是單射的。 它是滿射的嗎？ 作為對我們從輸入中學到的內容的自然推論，讓我們確定函式的值域。畢竟，確定某物是否為滿射的唯一方法是檢視值域是否適用於所有實數。確定這一點的一個好方法是找到涉及我們定義域的模式。假設我們將一個負數作為定義域的輸入：$f(-x)=a(-x)^{2}=a\cdot (-x)\cdot (-x)=ax^{2}$。這個看似微不足道的練習告訴我們，負數會為我們的值域提供非負數。這是一個非常重要的資訊！對於$x\in \mathbb {R}$，該函式總是產生$y>0$作為我們的值域。對於集合$B$，我們該集合中的元素沒有來自集合$A$的對映。因此，$y\leq 0$是集合$B$的陪域。因此，這個函式不是滿射的！

函式是數學的重要基礎。這種現代解釋是歷史上的數學家們辛勤工作的成果。直到最近，關係的定義才由勒內·笛卡爾在《幾何學》（1637 年）中引入。近一個世紀後，標準符號（$f(x)=y$）首次由萊昂哈德·尤拉在他的《無窮小分析引論》和《微積分原理》中引入。術語“函式”也是尤拉時代的一個創新，由戈特弗裡德·威廉·萊布尼茨在 1673 年的一封信中引入，用來“描述與曲線點相關的量，例如座標或曲線的斜率”。最後，函式作為集合之間關係的現代定義是由戈弗雷·哈羅德·哈代在 1908 年首次引入的，其中兩個變數$x$和$y$之間存在關係，使得“無論如何，對於一些$x$的值，都會對應一些$y$的值。”對於想了解更多關於函式歷史的人來說，這個頁面已經為您準備好了。

函式集合定義摘要

這部分可能是最難理解的部分。本章末尾提供了總結以幫助學生進一步理解。

• 笛卡爾積是操作 $A\times B=\{(x,y)|x\in A,\,y\in B\}$，其中 $A$ 和 $B$ 是兩個不同的集合。
• 對映是一種用 $f:A\to B$ 表示的關係，其中 $A$ 和 $B$ 是兩個不同的集合，使得笛卡爾積 $A\times B$ 產生有序對 $(x,y)$，對於任何給定的 $x\in A$，都對應到唯一的 $y\in B$。
• 函式是指將所有輸入的集合（即定義域） $A$ 對映到所有對應輸出的集合（即值域） $B$ 的對映，使得對於任何 $x\in A$，笛卡爾積只對唯一的 $y\in B$ 成立。
• 元素 $a\in A$ 是一個輸入。整個集合 $A$ 是定義域（因為它包含所有輸入）。對於任何 $r\in B$ 但 $r\notin R$ 並且 $b\in R$ 給出 $R=\{b\}$。 $R\subseteq B$ 意味著 $R$ 是值域，如果笛卡爾積 $A\times B$ 導致 $(a,b)$。集合 $B=R\cup \{r\}$ 是陪域。
• 令 $f:A\to B$。一個函式是單射的，當對於所有 $a_{1}\in A$ 以及 $a_{2}\in A$，如果 $f(a_{1})=f(a_{2})$，那麼 $a_{1}=a_{2}$。符號上，$\forall a_{1},a_{2}\in A\left(f\left(a_{1}\right)=f\left(a_{2}\right)\Rightarrow a_{1}=a_{2}\right)$。
• 如果對映$f:A\to B$ 的值域和陪域為$B$，則該函式被稱為滿射。換句話說，如果$f:A\to B$，則$f$ 被稱為滿射，如果$\forall y\in B\;\exists x\in A\left(f(x)=y\right)$.
• 如果一個函式既是單射又是滿射，那麼它被稱為雙射。

本節內容只使用專業術語。對於能夠理解和翻譯這些術語的學生來說，他們已經可以繼續學習“檢查你的理解”部分了。理解本節內容對學生來說至關重要，因為這些術語將會在後面再次出現，幫助學生更深入地理解複合函式和反函式的概念，我們將在適當的時候進行定義。此外，這些定義有時在證明中是必需的。對這些函式基本概念的良好理解將幫助學生在整個數學學習過程中受益，即使對於非數學專業的學生也是如此。

備註

以下內容是函式定義的直接結果

1. 根據定義，對於每個“輸入”，一個函式只返回一個與該輸入相對應的“輸出”。雖然相同的輸出可能對應多個輸入，但一個輸入不能對應多個輸出。這在圖形上表現為垂直線測試：一條平行於因變數軸（通常是垂直方向）的線只會與函式圖交於一點。然而，一條平行於自變數軸（通常是水平方向）的線可以與函式圖交於任意多個點。等效地，這在代數（或公式）解釋中也是如此。我們總是可以斷言，如果$a=b$ ，那麼$f(a)=f(b)$ ，但如果我們只知道$f(a)=f(b)$ ，那麼我們不能確定$a=b$ 。
2. 每個函式都有一組值，即函式的定義域，它可以作為輸入。這組值可能是所有正實數；也可能是集合{豬肉，羊肉，牛肉}。這組值必須在函式定義中隱式或顯式地定義。你不能將函式定義域之外的元素作為輸入，因為函式對於該輸入元素沒有定義。
3. 每個函式都有一組值，即函式的值域，它可以作為輸出。這組值可能是實數集。它可能是正整數集，甚至可能是集合{0,1}。這組值也必須在函式定義中隱式或顯式地定義。

這是一個不滿足垂直線測試的表示式示例。

垂直線測試

前文提到的垂直線測試是一種系統性的測試方法，用於判斷包含$x$ 和$y$ 的方程式是否可以作為函式（其中$x$ 為自變數，$y$ 為因變數）。只需將方程式繪製成圖形，並穿過$x$ 軸上每個點繪製一條垂直線。如果任何一條垂直線與圖形交於一點以上，則該方程式不是函式；如果該線始終與圖形交於一點或不交，則該方程式是函式。

（有很多有用的曲線，比如圓，不是函式（見圖）。有些人將這些具有多個交點的圖形，比如我們的圓，稱為“多值函式”；他們將我們的“函式”稱為“單值函式”。）