前言

這本書講述瞭如何設計 CPU 及其所有元件。我的 CPU 是一款普通的馮·諾依曼機，這意味著它按順序執行指令。我已經成功地使用 Xilinx CPLD 設計了一個 CPU，並且正在設計一個使用 Xilinx FPGA 的後續版本。之所以提到這一點，是因為我唯一能理解的程式語言是閘電路 CAD，而 Xilinx 有一個很棒的程式叫做 ECS，它使這成為可能。唯一的問題是，雖然我可以編寫純閘電路邏輯，但我不能編寫 ROM 函式，而這些函式是指令暫存器 (IR) 所需的，指令暫存器 (IR) 包含實現所有指令的微程式碼。這些在 6 塊 27C512 EPROM 中實現。但是，我認為可以使用 Verilog/VHDL 來實現，但我對這些語言一無所知，而且擔心將 ECS 與 Verilog/VHDL 結合起來會很困難，所以我的後續計劃仍然是使用外部 IR。我正在使用一種舊的架構，這意味著使用一種叫做累加器 (AC) 的東西，資料暫時儲存在那裡並進行操作，例如移位等。我將嘗試用這本書解釋你在 CPU 中需要使用的部分。

所選 CPU 架構

這裡有一些模組將在後面進行詳細講解。

FA：全加器，它是所有需要進行加法操作的核心（減法透過對二進位制補碼進行加法來完成）

CCR：條件碼暫存器，指示 FA 操作的結果，在 CCR 中設定不同的標誌。

SR：移位暫存器，我使用兩個 SR 來實現雙向移位，我稱它們為累加器 (AC)

SP：堆疊指標暫存器，該暫存器跟蹤進棧/出棧操作，是暫時儲存資料的另一種方法。

PC：程式計數器，它指出要使用的地址，是 CPU 的基本組成部分。

AR：地址暫存器，雖然 CPU 使用 8 位寬的資料匯流排，但地址匯流排是 16 位寬，因此需要兩個位元組來讀取和操作地址

AND：按位 AND

OR：按位 OR

XOR：按位 XOR

IRR：指令暫存器暫存器，該暫存器從程式記憶體中的資料匯流排上讀取傳入的操作碼，從而為指令暫存器 (IR) 設定地址，指令暫存器 (IR) 是 CPU 的真正大腦，因為它透過拉動大量的使能訊號來實現每個指令/操作碼，我的 IR 的資料寬度為 43 位 (IRR+BR+IRC 構成 IR 暫存器)。

BR：分支暫存器，該暫存器從 CCR 中獲取 N 和 Z 標誌，從而確定如何處理分支指令（以 CMP 型別的比較開頭）。

IRC：指令暫存器計數器，該計數器切換實現指令所需的地址，我將其限制為 16 步。

D：內部資料匯流排

A：內部 ALU 匯流排，這條額外的匯流排簡化了一些資料操作

OE：所有標有 OE 的方框都是三態緩衝器，在啟用時將它的值放在線上，否則處於高阻抗模式。

LD：所有標有 LD 的方框都是暫存器，它們儲存至少一個時鐘週期 (CP) 的資料。

累加器 (AC)

此圖展示了累加器的構建方式。累加器 A 和 B 只是移位暫存器，其中 A 用於將資料右移 (ROR)，B 用於將資料左移 (ROL)。不過我認為有些移位暫存器可以雙向移位，但我還沒有找到任何這種暫存器，因此採用了這種方法。這裡我使用了三個匯流排 (D/A/B)，但這並不是我在 CPU 中的設計方式，目前我不太理解為什麼使用三個匯流排。SA_A 代表移位到累加器 A 周圍，這意味著移出到右邊的位被放回到移位暫存器的左邊。Ain_A 是要移入移位暫存器的位，LDA（載入累加器 A）是將移位暫存器從 D 匯流排載入資料的指令。不同的 En 代表使能，使資料能夠傳輸到匯流排，停用則給出三態輸出。

移位暫存器

這個暫存器在上面被錯誤地命名為累加器 A/B，但它們是與我在本圖中顯示的型別相同的暫存器。我在 CPU 中使用這兩個暫存器來實現雙向移位。資料始終載入到兩個移位暫存器（參見體系結構），但取決於您希望向哪個方向移位，只有那個移位暫存器用於將資料輸入到內部匯流排。通常您無法購買 SR-觸發器/觸發器，而必須使用 JK-觸發器/觸發器，可能是因為 SR-觸發器/觸發器不允許輸入 11 作為輸入，而 JK-觸發器/觸發器允許（切換資料）。然而，可以使用 D-觸發器/觸發器來設計 SR-觸發器/觸發器，我認為我使用的是來自 Xilinx 庫的預定義 D-觸發器/觸發器。實際上，我嘗試使用普通 NAND 門在 ECS 中設計自己的正邊沿觸發的 SR-觸發器/觸發器，但儘管得到了 Xilinx 論壇的非常好的幫助，這仍然是不可能的。因此，我使用預定義的觸發器/觸發器。

Xn 是並行輸入，Qn 是並行輸出，LD（LDA/LDB）載入並行資料，x 是序列資料輸入（Ain/Bin），當 LD 為低且 En（使能）為高時序列資料被移位，當 LD 為高且 En 為低時並行資料被載入。我將 En 稱為 ROR/ROL，即右移和左移。

當進行微編碼時，這工作正常，因為您只需設定您想要的訊號，同時保持所有其他訊號為低電平，因此如果要移位，只需將 En 設定為高電平，LD 將為低電平，如果要進行並行載入，則將 LD 設定為高電平，而 En 將為低電平。

P 和 R 代表非同步預置和復位，低電平有效。

計數器

對於程式計數器 (PC)、堆疊指標 (SP) 和指令暫存器計數器 (IRC)，我們需要一個計數器。SP 也必須是向上/向下計數器，而其他兩個可能只是向上計數，但為了不使用向上/向下計數器使所有計數器都複雜化，因此我使用了向上/向下計數器。

因此，PC 和 IRC 始終只向上計數，但 SP 是一個特殊的計數器，用於指向與壓棧和出棧指令 (PSHA/PULA) 相關的 RAM 地址，以便能夠使用所謂的堆疊來儲存中間資料。您可能需要暫時儲存一些資料並在以後讀取，這時您會使用堆疊，而 SP 會跟蹤。

透過將載入 (LD) 拉高，它能夠將 Xn 資料並行載入到計數器中，輸出 (Qn) 的變化將在時鐘脈衝 (CP) 的正邊沿出現。當載入為低電平且使能 (EN) 和向上/向下' (U/D') 為高電平時，計數器向上計數，而如果 U/D' 為低電平，則計數器向下計數。

我使用了兩個時鐘，分別稱為 CP 和 E，其中 E 是反轉的 CP，這使得可以在 CP 正邊沿到來之前使用 E 設定計數器等。這在指令暫存器 (IR) 中對微指令進行程式設計時非常重要。

P 和 R 是非同步預置和復位，低電平有效。

指令暫存器計數器 (IRC)

我將這個計數器稱為指令暫存器計數器 (IRC)，這個計數器計算使用微程式碼實現每條指令的不同步驟。我將其限制為 16 個步驟，因此在最多 16 個時鐘脈衝 (CP) 內，必須實現指令。每個步驟實際上都是一個地址，資料寬度為 41 位。

程式計數器 (PC)

這個計數器被稱為程式計數器 (PC)，它是 CPU 的核心，因為它實際上是記憶體和輸入/輸出 (I/O) 的地址。它始終向上計數，因此 U/D' 為高電平。它可以使用載入 (LD) 設定一個新值/地址，如上所述。當使能 (En) 設定後，PC 隨著 CP 上升而計數。

堆疊指標計數器 (SP)

這個計數器稱為堆疊指標 (SP)，它指向一個小記憶體區域的地址，該區域使用 PSHA/PULA（將 A 壓入堆疊）/從堆疊中彈出 A 指令來臨時儲存資料，這意味著 PSHA 將累加器 A 資料儲存在 SP 指向的堆疊地址上，同時減少一個步長。如果要讀取資料，請使用 PULA 指令，指標將在讀取之前增加一個步長。SP 通常駐留在記憶體對映的底部附近，並且擁有一個相當小的記憶體區域，在我的情況下，它只有 256 位元組大 (0000h-00FFh)。

暫存器

暫存器在 CPU 中經常使用。例如，我將指令暫存器 (IR) 的地址部分用於暫存器，我將其稱為 IRR（指令暫存器暫存器），它是 IR 地址的一部分，由 IRR+BR+IRC 構成，其中 IRR 寬度為 8 位，BR（分支暫存器）寬度為 4 位，IRC（IR 計數器）寬度為 4 位。

暫存器用於臨時儲存資料，通常只儲存一個時鐘脈衝 (CP)。

當載入 (LD) 為高電平（且 CP 為高電平）時，Xn 是並行資料載入到暫存器中，然後 Xn 資料儲存在暫存器（或觸發器/觸發器）中，並出現在輸出 (Qn) 上。

P 和 R 是非同步預置和復位，低電平有效。

條件程式碼暫存器 (CCR)

條件程式碼暫存器 (CCR) 讀取全加器 (FA) 操作的結果。它識別操作是否為負（將 N 標誌設定為 1），或者是否為零（將 Z 標誌設定為 1）。它還告訴操作是否為所謂的溢位（將 V 標誌設定為 1）。它甚至會嗅探傳入的運算元是否為負。如果沒有 CCR，分支將無法執行。

指令暫存器暫存器 (IRR)

指令暫存器暫存器（IRR）是指令暫存器（IR）的第一部分，它從程式儲存器（以及資料匯流排）的內部 D 總線上讀取傳入的操作碼。IRR 是 IR 的一個重要組成部分，我將其稱為 IRR 只是因為缺乏想象力。

分支暫存器 (BR)

分支暫存器 (BR) 是指令暫存器 (IR) 的第二部分，它從條件碼暫存器 (CCR) 中獲取兩個標誌，分別稱為 N 和 Z，其中 N 檢查全加器 (FA) 操作（在比較（CMP）之前）是否變為負數或 FA 操作是否為零。這意味著如果 Z=1，則操作為零；如果 N=1，則操作變為負數。

我們可以這樣寫

NZ=00：操作不為負數且不為零（即為正數）

NZ=01：操作不為負數但為零（即為零）

NZ=10：操作為負數但非零（即為負數）

NZ=11：操作同時為負數和零（不可能發生）

指令暫存器 (IR)

指令暫存器 (IR) 由三個部分組成，即指令暫存器暫存器 (IRR)、分支暫存器 (BR) 和指令暫存器計數器 (IRC)，總共 16 位寬。這些模組都是暫存器，除了 IRC 是一個計數器，它們共同構成了指令暫存器 (IR) 的地址。此地址隨後設定高達 41 個數據位，這些資料位隨後在 CPU 內部使用，以在不同的使能訊號、載入等中來實現不同的指令。所有這些資料位都非常關鍵，但其中兩個尤其重要，它們是 Ready 和 Branch 位。Ready 訊號表示指令已完成，而 Branch 訊號表示有分支。當操作碼為分支時，必須從條件碼暫存器 (CCR) 中獲取資料，以便 IR 知道該怎麼做。

地址暫存器 (AR)

地址暫存器 (AR) 設定來自程式計數器 (PC) 或內部（擴充套件定址模式）的地址。我為每個位元組使用一個暫存器，因為資料匯流排 (DB) 只有 8 位寬，而地址匯流排 (AB) 有 16 位寬。實際上，位元組是按順序載入的，這意味著在載入完兩個位元組之前，地址都是無效的。在這個單個時鐘脈衝 (CP) 持續時間內，AR 地址“隨機”變化，但這並不重要，因為只有在完成時才會進行讀或寫操作。也許在 AR 之後再新增一個包含高位元組 (HB) 和低位元組 (LB) 的暫存器會更整潔。

資料匯流排 (DB)

資料匯流排 (DB) 是一個雙向匯流排，實現起來有點難。我以為我已經驗證了它可以在兩個方向上工作，但事實並非如此。雖然我可以執行 JMP 指令，但我知道資料是從資料匯流排進入的，因為從程式儲存器（以及 DB）中正確讀取跳轉地址並載入到程式計數器中，設定跳轉地址。上面的架構相當準確地展示了資料匯流排的實現方式。它使用兩個反向並聯的 3 態緩衝器，高 R/W' 使能資料寫入 CPU，低 R/W' 使能資料寫入外部儲存器或 I/O。此外，還有一個重要的特殊訊號，我將其稱為 D_REL，此訊號以這樣一種方式釋放內部 D 匯流排，使得 D 匯流排可以在內部使用來迴圈內部資料。

全加器 (FA)

我使用的全加器 (FA) 如圖所示，根據卡諾圖，輸出/和為

$s_{i}=c_{i}'x_{i}'y_{i}+c_{i}'x_{i}y_{i}'+c_{i}x_{i}'y_{i}'+c_{i}x_{i}y_{i}=c_{i}\oplus x_{i}\oplus y_{i}$

對於進位生成，我們有

$c_{i-1}=x_{i}y_{i}+c_{i}y_{i}+c_{i}x_{i}=x_{i}y_{i}+c_{i}(x_{i}\oplus y_{i})$

但是，此表示式是一個修復，因為如果 ci 為高，那麼 xi 或 yi 為高就足夠生成進位，在這種情況下，xi 和 yi 都為高並不重要。

FA 在 CPU 中一直使用，很少有指令不使用 FA。邏輯指令，如 AND/OR/XOR 以及堆疊和子程式指令以及累加器值的載入/儲存（LDA/STA），是我能想到的為數不多的幾種指令。大多數指令都使用 FA，例如分支、遞增 (INCA)、遞減 (DECA) 以及加法/減法。

然而，在 CPU 中，我們不僅要加，還要減。人們發明了一些有趣而實用的東西，那就是二進位制補碼。用一個數的二進位制補碼進行加法，實際上可以得到減法！

因此，我們不需要額外的全減器 (FS)，而是可以用一個數的二進位制補碼進行加法來進行減法。

分支偏移量以二進位制補碼形式寫入，這使得程式計數器向後跳轉。

一個數的二進位制補碼是透過對所有位進行反轉並加 1 來建立的，它實際上是一個數字迴圈，如果我們使用 4 位的資料寬度進行簡化，那麼正數從 0000b 到 0111b，負數從 1000b 到 1111b，其中 1111b 等於 -1。

最高位仍然表示負數（就像使用帶符號表示一樣），但在這裡迴圈中的數字方向相反，即當正數增加到 7h 並回滾到 8h 時，該數變為負數，值為 -8，而“abs”隨著值達到 Fh（等於 -1）而減小。

進位生成延遲了兩個 tpd（每個門的傳播延遲），對於我的 8 位資料，總延遲為 16 tpd。這對於我的 CPU 的執行速度至關重要。雖然 FA 必須完成，tpd 的量級為 5ns，那麼最大時鐘速度（使用對稱時鐘，即兩個“tpd”）為 6MHz，我的 CPU 無法執行得比這更快。然而，有一種稱為“進位加速”的技術，但這對我來說無關緊要。

選定的指令 (CPU 彙編指令)

這張圖顯示了選定的指令。我決定跳過底部的兩條指令，部分原因是堆疊指標 (SP) 實際上是在啟動時初始化的（POR，或加電覆位），並且沒有必要更改它（POR 將其設定為 00FFh）。操作碼是從 HCS08 中借來的，目的是不必設計自己的編譯器，不過可以用純機器程式碼程式設計，這也是我的目標。我選擇的指令儘可能少，以使我的 CPU 更簡單（也稱為 RISC，即精簡指令集計算機）。

我在 CPU 中使用的定址模式包括立即定址、擴充套件定址和固有定址。立即定址意味著資料直接從外部程式儲存器中讀取，在圖中用“dd”表示。擴充套件定址意味著資料從 RAM 或 I/O 中讀取，此資料型別可以稱為變數，並用“hhll”表示，表示運算元是兩個位元組長（h 表示高位元組，l 表示低位元組），因為該值實際上駐留在一個 16 位地址中。固有定址意味著我們不需要運算元，例如 INCA 僅將累加器 A 中的值加 1。

實際上，還存在另一種“定址模式”，它有點特殊，因為只有分支指令使用它。它在圖中用“rr”表示，這是一個補碼形式的相對數，它在我們需要 CPU 根據條件跳轉到某個地方時，設定程式計數器 (PC) 的跳轉。

分支跳轉

此圖展示了相對分支跳轉是如何完成的。例如，如果 PC 位於 28h 處，並且偏移量 (rr) 為 F8h（使用反轉 + 1 我們得到 -8），那麼 PC + 偏移量的補碼加法結果為 20h，這意味著 PC 跳轉到 20h 處。這裡我們還可以看到，當第一個“位元組”相加時會產生進位（因此加法必須使用 ADC，帶有進位的加法）。如果 PC 位於 26h 處，並且 rr 為 +3，那麼 PC 的跳轉地址為 29h，但這裡 V 標誌被置位，在這種簡化的情況下，這個溢位標誌與低位元組的值大於 7h 有關，在正常情況下，這意味著位元組值超過 255。如果 PC 位於 26h 處，並且我們希望新增 -8，最終將到達 1E。我找不到任何問題，但已經實現了兩個 EP 訊號，ADD_00 和 ADD_FF，用於表示 rr 是正數還是負數。我認為我考慮得太多了，因為圖中顯示了使用 rr 的普通補碼加法可以正常工作。

補碼非常有趣。如果你想象一個圓圈，其中 0h 位於頂部，只要數字是正數，它就會順時針 (CW) 傳播，並在 7h 處停止。在 0h 的另一側，我們有 Fh，它表示 -1，然後這個值負向增加，從圓圈的另一側逆時針 (CCW) 移動到 8h，它表示 -8，而 Fh 表示 -1。將圓圈看作一個時鐘，正數隨著時間的推移而增加，負數（不帶符號）隨著時間的推移而減少。

CPU 定時

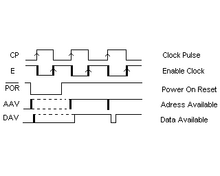
此圖展示了我的 CPU 的定時。E 時鐘是 CP 時鐘的反相，但它被延遲了（但延遲不多，通常 <10ns，也稱為 tpd，即傳播延遲）。實際上，我把 E 時鐘稱為 EP 脈衝，因為它控制著指令暫存器 (IR) 的地址，從而在一個完整的時鐘週期 (T(CP)) 內使能資料。這意味著它在一個完整的 CP 週期內使能資料。在 EP 期間，資料被使能，拉動所有資料“引腳”，但實際上在 CP 變高之前不會發生任何事情，而 CP 變化發生在 EP 的中間。因此，在 CP 來臨時，EP 期間的資料是穩定的。資料可用 (DAV) 只是表明，當設定地址時，資料可用之前有一個很小的延遲 (tpd)。我透過使用 E 時鐘來規避這個事實，E 時鐘有一個延遲，它等於 CP 時鐘週期時間的一半，產生一個 T(CP)/2 的延遲，如果 CP 頻率不是太高，這足夠了。

微程式控制

此圖展示了微程式控制是如何完成的。指令暫存器 (IR) 中的每條指令都有 16 位的地址寬度和 43 位的資料寬度。每個資料位設定或停用內部暫存器的不同載入 (LD) 和緩衝區的不同輸出使能 (OE)，以及一些關鍵訊號，例如堆疊指標 (SP) 是否應該遞增或遞減。每行由 E 時鐘設定，CP 在行邊界處執行，我在下面將這些訊號重新命名為 EP 脈衝和 EC 時鐘，它們分別代表 E 時鐘脈衝 (EP) 和執行時鐘 (EC)。在進行微程式控制時，這一點非常重要。

復位 (RST) 是一條僅在復位時執行的內部指令。它在 IRR 中有一個操作碼 (op-code) 等於 00h，這是在 POR（即 IRR 暫存器被設定為 00h）時發生的事情，一切從那裡開始。在 POR 時，PC 初始化為 FFFEh（指向起始地址的 HB 部分）。透過將 LD_AR_HB 和 LD_AR_LB 設定為高電平，這個地址在下一個 EC 時鐘的上升沿被載入到 AR 中，成為一個實際地址（FFFEh 成為地址）。在下一行，R/W' 被設定為讀操作，並且 LD_PC_HB 被設定為載入 FFFEh 處的跳轉地址的高位元組，當 EC 時鐘到來時，跳轉到的地址的 HB 被讀取（並載入到 PC_HB 暫存器中）。同時，PC_EN 被設定為能夠為下一個復位位元組增加 PC（PC_LB）。當下一個 EC 時鐘到來時，AR 更新為新的地址 (FFFFh)，其中包含跳轉地址的 LB。在這行，我設定了 LD_PC_LB 並使能讀操作。現在 PC_HB 和 PC_LB 暫存器都包含了正確的跳轉地址，該地址是實際程式開始的地方。現在我們所要做的就是將跳轉地址傳輸到地址暫存器 (AR)，我透過在最後一行將 LD_AR_HB 和 LD_AR_LB 設定為高電平來完成這一點。

在進行微程式控制時，有很多事情需要考慮，我正在考慮對 R/W' 進行反相，使其不再幾乎總是為 1。這也意味著 R'/W 實際上與 OE' 相同，這就是儲存器想要的，並且微程式控制被簡化了（使用盡可能少的 1）。當然，CS_I/O 也必須進行修改。

下面我展示了一些非常重要的指令的微程式控制，沒有這些型別的指令，CPU 就毫無意義。

LDA 微程式控制

LDA 代表 LoaD Accumulator A，這是最有趣的事情發生的地方。LDA 有兩種模式，它可以在所謂立即模式（LDA#）下直接從程式儲存器中讀取資料，或者它可以在所謂擴充套件模式（LDA$）下從地址讀取資料，當然微程式控制是不同的。

STA 微程式控制

STA 指令的 CPU 微程式控制

STA 代表 STore accumulator A。這條指令只能將資料儲存到指定地址（即 RAM 或 I/O），這通常被稱為擴充套件模式。

BEQ 微程式控制

BEQ 代表 Branch if EQual。這種型別的指令非常重要。如果沒有分支指令，CPU 無法做太多事情，因為分支指令是讓 PC 根據條件跳轉到所需位置的一種方式。例如，如果你有一個條件，你想讓 CPU 重複程式碼的一部分，你只需等待 Z 標誌被置位，只要它沒有被置位，指令就會重複執行（即只要操作不為零）。

這條指令不起作用，我已經嘗試過了。所以不要太關注我的原理圖，除了可能識別基本原理。我在下面給出了一個關於同一指令的更具教學意義的示例，我認為它可能起作用。

簡化的 BEQ 微程式控制

我花了一些功夫去理解分支 BEQ 是如何實現的。我把它做得更具教學意義，雖然很多位可以同時被設定，但這樣我就可以描述每個步驟。儘管如此，這個版本也是我實際可以使用的版本，因為步驟的數量正好等於 4 位 IRC（指令暫存器計數器）可以處理的步驟數量。在微程式控制方面，我決定，CP 時鐘的更合適的名稱實際上是 EC 時鐘或執行時鐘，因為我的原理圖中向下每一行的邊界都表示由 EC 執行，行本身使用 E 時鐘，我決定將其稱為 EP 脈衝，而在 IR 內部，它實際上是一個持續時間為整個 CP 週期時間的脈衝，每一行只是顯示了將要發生的事情，而 EC 發生在 EP 的中間，而 E 時鐘只是一個反相的 CP 時鐘。換句話說，EC 在資料有效時對資料進行時鐘控制，因為所有 OE/LD 等等都有一個傳播延遲，必須等待它過去。

對於所有分支指令，必須在執行任何操作之前讀取 NZ 標誌的狀態。在本例中，NZ 標誌必須指示 Z=1 表示零，而所有其他組合必須被忽略。但是，所有其他組合（除了 NZ=11，這種情況不可能發生）必須被處理，並且只是增加程式計數器 (PC)，使其指向下一個操作碼/指令。

我版本的 BEQ 微程式控制

這裡我要對 R/W' 進行反相，使其不必總是為 1，然後我將嘗試減少 IRC 步數，因為很多事情實際上可以同時啟用。也許我們可以稱之為“前瞻”。我不追求速度快的 CPU，我只是希望它能夠工作，但如果我能減少 IRC 步數，我會很高興。

儲存器對映

這張圖展示了我的記憶體對映，即我如何使用可用的 65kB 地址空間來分配不同的記憶體和 I/O。它還相當精確地展示了我如何編碼不同的片選 (CS)。X-TAL (CP) 和復位已重新設計。對於 CP，我使用三個時鐘，一個是使用帶有開關的 SR 閂鎖的“DC 時鐘”，另一個時鐘是使用施密特反相器產生的 1Hz 自動時鐘，最後一個是我幼稚的施密特 1MHz 時鐘。我只嘗試過後兩種時鐘。

主機板

為了測試 CPU，必須使用某種主機板。我使用了以 nibble 為單位排列的普通 LED，高 nibble 使用紅色，低 nibble 使用綠色，以便更容易讀取十六進位制程式碼。我還使用了兩個外部儲存器，一個是程式儲存器 (ROM)，另一個是 RAM 儲存器（工作儲存器？），用於臨時儲存資料。我還使用了一個位於 16kB 地址空間內的單一地址，用於讀寫 I/O 資料。換句話說，我的主機板/計算機不會有滑鼠，而是僅與鍵盤和顯示器互動，在原型階段，顯示器僅由兩個十六進位制開關組成，用於模擬鍵盤，以及一個原始顯示器，所有資料都由我的 LED 顯示。

第一塊主機板

這塊舊主機板是我第一塊使用 Xilinx CPLD 的 CPU 的主機板。它非常詳細，因為主機板是手工搭接的，沒有 CAD 程式的幫助。

新主機板

這塊新主機板是為我的 Xilinx FPGA 版本設計的。它沒有那麼詳細，因為我計劃使用 CAD 程式。可能不會使用我目前使用的 Eagle，這是因為我的免費 Eagle 版本無法處理我需要的如此大的 PCB。我計劃使用 KiCAD 代替。實際上，I/O 鍵盤 (KB) 和顯示器 (DSP) 將在位置上互換，因為如果開關最靠近你，則“手動時鐘”更簡單。

新版本

我決定分步進行。我將只複製第一塊主機板，並新增一個輸出停用 EPROM 的可能性，以便可能（觀察）將 EPROM 整合到 Spartan 中。I/O 可能性將被省略，我將只專注於驗證指令。如果（觀察）我設法驗證了所有 33 條指令，我將設計一塊新的主機板，以便能夠構建自己的計算機。來自 5V 外部儲存器（和其他）的所有訊號都將串聯 100 歐姆電阻連線到 Spartan（但我有點不確定這是否足夠，我認為這取決於外部 IC 的電流能力）。

CPU 測試電路

這張圖展示了我們 CPU 的測試電路。二進位制值由兩個十六進位制開關設定（MSB 最上面）。在執行此操作時，該值將由最左側的 LED 記錄。當你設定了想要的值後，按下瞬時開關 SW1。然後，該值將被時鐘到最左側的下一個 LED 陣列。然後，CPU 在有空時讀取該值，並透過 HC374 將該值呈現給 CPU，HC374 是一個並行可載入暫存器。如果我們將這個暫存器（一個八進位制 D 型觸發器）稱為 IC2，那麼進入 IC2 的值會在片選 (CS) 和 R/W' 為高時傳播到資料匯流排 (DB)。如果 R/W' 為低，則寫入的值會傳播到較低的暫存器 (IC3)，該暫存器始終處於啟用狀態，它只是嗅探資料匯流排。正如我們在上面的記憶體對映中配置的那樣，我們可以寫入和讀取到同一個地址（例如 $4000），並且在讀取時獲取來自十六進位制開關的值，並在寫入時點亮我們原始顯示器的 LED。這意味著不能使用滑鼠，只能使用鍵盤和某種顯示器。

我們還添加了一些 LED 指示燈，用於指示地址匯流排 (AB) 和資料匯流排 (DB)，以及 CS 和 R/W'（指示 R/W' 的高電平和低電平）。如果你想使用這些指示燈，你必須是十六進位制程式碼專家（所有 LED 都分成四組，使用紅色表示高 nibble，綠色表示低 nibble，以簡化操作）。

然而，在擴充套件定址模式下，地址設定方式存在一個學術問題，因為地址是每次設定一個位元組的。但是，微指令將在地址設定完成後結束，因此理論上你只會在一個時鐘週期內獲得一個錯誤的地址，該地址在那個時鐘週期內是錯誤的。

CPU 介面卡

KLD_F 是我的主機板專用的 PCB 介面卡。這種方法的優點是你實際上可以使用任何你想使用的 CPU（只要它是 8x16）。你只需要一個專用於你的特定 CPU 的介面卡 PCB。我已經為我的 Spartan FPGA 設計了一個 PCB 介面卡，其封裝稱為 PQ208（即它有 208 個引腳）。問題在於我的 Spartan 的可用性，很難找到。所有好東西都在不斷變化，因此能夠使用任何封裝的概念非常棒。我實際上計劃設計另外兩個介面卡 PCB，我將第一個稱為 KLD_D，用於 DIL 型處理器（如 MC6809），另一個將稱為 KLD_H，用於 PQ44（HCS08）。甚至可能有一個針對 BGA 的版本。

閘電路技術

如果我們算上三態門，我們就有七種不同的邏輯閘，我將在下面使用 TTL（電晶體電晶體邏輯）描述它們，而普通的 DTL（二極體電晶體邏輯）在某種程度上更有教學意義。真值表和閘電路符號都已顯示。所有閘電路符號都採用歐洲標準。

非門（反相器）

這張圖展示了一個非門。當輸入為高電平時，輸出為低電平，反之亦然。

與非門

這張圖展示了一個與非門。當所有輸入都為高電平時，它為低電平，否則為高電平。計算機中的所有東西，除了硬碟驅動器 (HD) 或一些永久性儲存器，都可以用僅用與非門構建！

或門

這張圖展示了一個或門。當至少一個輸入為高電平時，該門為高電平，否則為低電平。符號 >1 並不完全正確，因為它應該讀作 >=1，但很難放入符號中。

與門

這張圖展示了一個與門。當所有輸入都為高電平時，該門為高電平，否則為低電平。

或非門

這張圖展示了一個或非門。當所有輸入都為低電平時，該門為高電平，否則為低電平。計算機中的所有東西，除了硬碟驅動器 (HD) 或一些永久性儲存器，都可以用僅用或非門構建！

異或門

這張圖展示了一個異或門。當輸入為高/低或低/高時，該門為高電平，否則為低電平。這意味著一個輸入為高電平，另一個輸入為低電平，反之亦然，都會產生高電平輸出，所有其他組合都會產生低電平輸出。我使用上面的符號來顯示這個門。看到一個離散版本會很有趣。

三態門

此圖展示了三態門。該門與非門類似，當輸入為低電平時為高電平，反之亦然。但是，在這種情況下，OE（輸出使能）訊號必須為高電平。當 OE 為低電平時，輸出為高阻抗，在此狀態下，訊號可以被應用於輸出。這對 CPU 內部（或外部）的匯流排系統至關重要。

觸發器技術

下面我將展示如何構建觸發器及其一些關鍵元素。

險象生成器

此圖展示瞭如何生成用於邊沿觸發觸發器的險象。險象是基於門的傳播延遲 (tpd) 生成的。左側的圖因此在輸入訊號變為高電平時會產生一個負險象，這是因為當穩定的輸入為 0 時（NAND 引腳上的 01），NAND 門為高電平。但是當輸入變為高電平時，反相器會在很短的時間內（tpd）保持高電平，因此 NAND 門的淨輸入為 11，從而產生險象。右側的圖以相同的方式工作，但會產生一個正險象。

險象的持續時間可能不足以設定例如 POR 時的計數器，但如果脈衝太小，可以將電容器安裝到反相器輸出端以產生更大的險象。也可以串聯多個反相器以獲得更大的險象。

觸點抖動消除器 (SR 觸發器)

此圖展示了幾個交叉的 NAND 門。它們實際上是一個 SR 觸發器形式的儲存單元（注意輸入被反轉）。假設 SW 處於較低位置，那麼 Q' 將保證為高電平，而 Q 將為低電平，因為上 NAND 門的兩個輸入都為高電平。當 SW 切換位置時，Q 變為高電平，Q' 變為低電平，因為下 NAND 門的兩個輸入都為高電平。當 SW 處於空中時，保持前一種狀態（由於 S'R'=11），並且狀態切換僅進行一次。這意味著觸點抖動被消除了。

如果您希望將開關連線到處理器，此設定非常有效。因此，您無需使用濾波器或特殊例程以軟體方式過濾輸入訊號。缺點是開關需要雙擲，這使得普通簡單的按鈕失效。

邊沿觸發 D 型觸發器

此圖展示了一個正邊沿觸發 D 型觸發器的架構。每次 CP 的正邊沿到來時（因為它根據上述內容生成一個險象），D 輸入的值就會被傳輸到輸出 (Q)。您可以移除輸入反相器以獲得 SR 觸發器。這是數位電路中最簡單的儲存元素。74HC74 是一個正邊沿觸發 D 型觸發器，可以以這種方式設計。

我嘗試用 Xilinx 用於門 CAD 的優秀程式（稱為 ECS）使用此方法，但不幸的是它無法實現，因此我所有的 SR 觸發器都是預定義的。但是我認為我的方法是可行的。

可預置 D 型觸發器

此圖展示了一個正邊沿觸發 D 型觸發器，帶有非同步預置和清零。因此，可以使用 R' 和 P'（低電平有效）觸發觸發器。這些訊號在使用前必須釋放到高電平，但它們是“POR”觸發器狀態的完美方式。POR 表示上電覆位。

SR 觸發器

此圖展示了一個 SR 型觸發器及其真值表。它是 D 型觸發器的簡化版本。真值表應解釋為其中的值是下一個值。SR=11 不允許。

D 觸發器

此圖展示了一個 D 型觸發器及其真值表。它在 CPU 中最常使用。

JK 觸發器

此圖展示了一個 JK 型觸發器及其真值表。JK 觸發器是 SR 觸發器的擴充套件版本，它包含反饋。JK 觸發器比 SR 觸發器有優勢，因為它對所有型別的輸入都有定義。在 JK=11 時，它會翻轉。它也可以作為封裝購買，而 SR 觸發器我沒有找到。

T 觸發器

此圖展示了一個 T 觸發器及其真值表。T 觸發器可以在 T 為高電平時將時鐘脈衝 (CP) 的頻率減半。當 T 為低電平時，什麼也不會發生。實際上，T 輸入短接了 JK 輸入，並控制輸出是否應該翻轉。下面我將展示一種更簡單的 CP 頻率劃分方法。

頻率劃分器

此圖展示瞭如何將時鐘頻率 (CP) 劃分為二。它基於 D 型觸發器構建。所述觸發器每次 CP 變為高電平時都會改變狀態。這是因為 Q' 已連線到 D 輸入，因此如果 Q 為 1，則 D 會被提供 0，這會使 Q 在 CP 的下一個正邊沿變為低電平。因此，一個週期需要兩個邊沿，這使得頻率成為 CP 的一半。

RAM 記憶體

此圖展示瞭如何構建 RAM 記憶體中的單個單元格。因此，使用一個普通的觸發器（在本例中為 D 型觸發器）儲存了一位資訊。這使得記憶體速度非常快。但同時，當沒有電源時，它會丟失資訊。它的功能是透過地址進行定址，如果 R/W'（讀寫）為高電平，則讀取資料，如果 R/W' 為低電平，則寫入資料。由於資料輸入和資料輸出共享相同的匯流排，因此沒有顯示整個儲存單元，因為我們還需要幾個三態門。

雜項門技術

這裡我將展示您如何使用不同的門配置。

單穩態多諧振盪器

此圖展示了一個單穩態多諧振盪器。單詞“單”表示只有一個穩定狀態。該電路由觸發輸入 B' 上的負邊沿觸發，這會使輸出 Q 變為高電平，持續

$T=0,72RC$

秒，這當然只對 4538 有效，但原理對所有電路都是相同的。

無穩態多諧振盪器

此圖展示了一個無穩態多諧振盪器。它沒有穩定狀態，因此它會一直改變狀態。通常，我使用一個施密特反相器（通常是 HC14）來設計我的無穩態多諧振盪器。可以證明，該電路的頻率為

$f_{0}={\frac {1}{2RC\ln {3}}}$

但是對於一個單獨的 4093 Schmitt NAND，我計算出

$f_{0}={\frac {1}{1,24RC}}$

當以 Vdd=5V 驅動時，其中電源 (Vdd) 對精確頻率至關重要。

多路複用器

這張圖展示了一個多路複用器 (MUX)。圓圈表示反相，& 表示與門，>1 表示或門。藉助於控制訊號 ABC，可以選擇哪個輸入處於活動狀態並將訊號傳遞到輸出。例如，如果控制訊號為二進位制 110，則輸入 6 處於活動狀態。74HC251 是一個 8 通道多路複用器。

譯碼器

這張圖展示了一個譯碼器或反多路複用器。它由多個與門和多個反相器構成。譯碼器實現了輸入訊號的所有組合。例如，如果 ABC 為 011，則與門編號 3 處於高電平。74HC138 是一個 3 到 8 線譯碼器。

比較器

在 CPU 中，比較兩個數字的需求很常見。假設 X=<x1, x2,...,xn> 和 Y=<y1, y2,...yn>，目標是指示 X=Y 或 X>=Y、X>Y、X<=Y 中的一種情況。我們注意到 X>=Y 是 X<Y 的反相，因此我們只需要考慮兩種情況（同時變數也可以互換）。

$X=Y$

和

$X<Y$

基本比較器

這張圖展示了一個基本比較器，因為 xi=yi 透過一個簡單的異或門和一個反相器來實現。當兩個訊號都為高電平或都為低電平時，輸出為高電平，因此當它們相等時輸出為高電平。

X=Y

這張圖展示了一個用於 X=Y 的 4 位比較器。如果任何一對位不同，它們的異或門將產生一個高電平訊號。當比較數字時，檢查任何一個異或門是否處於高電平就足夠了，因為這意味著數字不相等。如果任何一個異或門處於高電平（即表示這對位不相等），則非門處於低電平，這意味著如果非門處於高電平，則數字相等。

X<Y

這張圖展示了一個用於 X<Y 的比較器。如果從最高位開始，觀察到 x1'y1=1，則立即有 X<Y。如果 w2=x1'+y1=1（這意味著 x1y1=00、01 和 11，因此相等或小於）並且 x2'y2=1，則也有 X<Y。因此 Wi 表示需要檢查下一位，看看 xi<yi 是否成立。

ALU 元件

ALU 代表“算術邏輯單元”，是 CPU 中執行算術計算（尤其是加法和減法）的部分。

基本加法器

這張圖展示了一個基本加法器，它是一個單獨的異或門。兩個一位數字的加法在透過異或門後就完成了。但是缺少兩件事，第一是進位產生，當兩個數字都為高電平時，這是一種溢位。進位產生可以透過一個使用與門的簡單加法器來實現，該與門在兩個位上工作。這可以用 1+1=0 表示，進位為 1（由於與門），用於下一位。全加器 (FA) 還會處理是否從低位加法中產生了進位，並將此高電平訊號（當進位時）傳遞到下一個單元。我認為這個事實很簡單，就像如果最低位都為高電平，則按位加法為零，但有進位。現在進位被加到下一位，使進位和按位加法為二進位制 10（即 2），如果還要加進位，則結果為二進位制 11（即 3），因為按位加法（包括進位）現在為 1。我對這一點有點不確定，但它確實有效。也許你可以把它看成是每次加法實際上都是一個異或運算，因此如果兩個位都為高電平，則異或運算產生一個低電平輸出，將進位和此輸出輸入到一個新的異或運算，使訊號變為高電平。

全加器 (FA)

我已經在上面描述過了，但為了連續性在這裡顯示它。雖然我已經描述過它了，但我只是提供和與進位產生的公式（這些訊號來自使用卡諾圖的影像）。

$s_{i}=c_{i}'x_{i}'y_{i}+c_{i}'x_{i}y_{i}'+c_{i}x_{i}'y_{i}'+c_{i}x_{i}y_{i}=c_{i}\oplus x_{i}\oplus y_{i}$

和

$c_{i-1}=x_{i}y_{i}+c_{i}y_{i}+c_{i}x_{i}=x_{i}y_{i}+c_{i}(x_{i}\oplus y_{i})$

全減器 (FS)

這張圖展示了一個全減器 (FS)，它的理論和實現。假設數字是正數。如果數字是

Y=<y1, y2,...,yn>

和

X=<x1, x2,...,xn>

從 X 中減去 Y（D=X-Y）。

我不會深入研究這個問題，因為減法通常使用二進位制補碼加法來完成。但是，我的圖中“清楚地”顯示了這個原理，但我不會描述它，因為我的英語水平不是很好。但是，我將強調結果是二進位制補碼，並向您展示公式。

$d_{i}=x_{i}\oplus y_{i}\oplus d_{i}$

和

$b_{i-1}=x_{i}'y_{i}+b_{i}(x_{i}\oplus y_{i})'$

永久儲存器 (ROM)

CPU 需要某種永久儲存器（ROM，只讀儲存器）來獲取指令。然而，這種 ROM 只能程式設計一次。我使用 6 個 EPROM（27C512）作為我的指令暫存器（IR）和一個作為程式儲存器。由於使用的是 EPROM，如果需要，我可以重新程式設計它們，因為我並不擅長。

基本 ROM

這幅圖展示了一個基本的永久儲存器（ROM），它使用與門和或門來實現。X 表示 3 位地址匯流排，W 表示選擇的字線，b 表示位，也就是資料匯流排。如果地址是 010（w2），則資料是 0110。

NAND-NAND 結構的 ROM

這幅圖展示了一個 ROM，它可以稱為 MROM，即機械可程式設計只讀儲存器。在這裡，二極體被用於你想要設定為高的位置。因此，如果地址仍然是 010，那麼 W2 將為低電平，連線到 W2 的所有二極體將向輸出反相器提供低電平輸出，使其輸出為高電平。因此，我們與上述情況相同，但在這裡我們可以使用二極體設定我們想要的資料。然而，一個 8 位資料輸出（匯流排）最多需要 256 個二極體。所以這種 ROM 只能滿足窄匯流排（或者如果資料大多數情況下是低電平），但它有效！

可程式設計邏輯陣列 (PLA)

這幅圖展示了一個 PLA，它是一個可程式設計的永久儲存器或 PROM（可程式設計只讀儲存器）。程式設計非常簡單，因為在與部分和或部分都使用了二極體功能。對於非常小的儲存器，可以使用二極體進行程式設計，如所示。如果我們看 w0，我們可以看到 x1'x3=1 選擇它為高電平，現在 b1 和 b2 在或部分為高電平，這僅僅意味著資料輸出可以使用二極體進行“或”操作。

我認為 PLA 是所有型別可程式設計電路（如 CPLD 和 FPGA）的更平滑的名稱。

實現

一個非對稱的 8x16 位架構（一個不對稱的架構，意味著它在中心軸兩側沒有映象）被認為是最佳的，因為程式可以以清晰的方式編寫（讀取兩個十六進位制符號表示資料，四個表示地址），並且很容易獲得外圍電路，例如 EPROM 和 RAM 等。也沒有什麼可以阻止人們擴充套件到任意非對稱架構模型 16x32。唯一的障礙可能是外圍電路。無論如何，人們可以利用所選架構走得很遠，例如，一個典型的 32kB 大程式，不僅僅是一個演示的角度來看。非對稱架構的唯一問題是處理器比必要時稍微複雜一些。

高階架構

這幅圖展示了我第一次嘗試設計 CPU。這款 CPU 還實現了索引暫存器（X-Reg）。我個人沒有看到使用索引暫存器的真正意義，所以它在下面更簡單的 CPU 中被刪除了。有趣的是，索引暫存器直到 1949 年之後才開始使用（根據維基百科）。然而，根據我目前的知識，累加器 A（ACC_R + ACC_L）已被準確地實現。據我所知，累加器是三件事：可並行載入的暫存器、移位暫存器和資料的中間儲存器。移位暫存器功能透過使用 LSL（邏輯左移）進行乘法或使用 LSR（邏輯右移）進行除法來使用，其中只有乘以 2 的冪和除以 2 的冪是可能的（左移一次意味著乘以 2，右移一次意味著除以 2）。因此，MUL 和 DIV 在正常的 CPU 中以硬體方式實現。使用 LDA（載入累加器 A）的儲存功能是最常見的，當需要將值寫入 RAM 或 I/O 時，你執行 STA（儲存累加器 A）。

簡單架構

在這個更簡單（並且使用）的架構中，我們刪除了索引暫存器，刪除了清除進位 (C_CL) 的可能性，並將累加器 A 簡化為僅包含兩個可並行載入的移位暫存器 (SR_R 和 SR_L)，也簡化了堆疊指標暫存器 (SP)。刪除 C_CL 的意義在於，將製作兩種型別的加法指令，一種是普通的 ADD，它將兩個整數相加，不考慮進位（儲存在 CCR 中），另一種是 ADC（帶進位相加），它將兩個數字相加，考慮進位（意味著如果前一次加法產生了進位，則將考慮進位）。所以，如果你例如將 PC_LB 與一個相對的（二進位制補碼）分支跳轉（例如 BEQ）相加並得到進位輸出，那麼你就可以新增 0+C+PC_HB（透過設定 ADD_00+ADC）並得到新的 PC_HB 輸出。0 來自於加法必須相對於某物進行（加法器有兩側）。由於我們簡化了操作，簡單的指令 INCA（累加器 A 加 1）和 DECA（累加器 A 減 1）必須使用全加器 (FA) 來完成。這可以在微指令級別完成，例如，首先我們將累加器 A 載入為例如值 $FE，然後該值使用訊號 ALU 放置到 ALU 總線上（並且可以在 FA 的頂部訪問），然後 ADD_01（在 FA 的底部）被設定為高電平（而 ADC 被設定為低電平），這意味著 $01 被新增到 ALU 總線上的值（因此累加器 A 中的值）。在下一個時鐘脈衝 (CP) 時，累加器 A 被載入為增加後的值（這裡 LDA 為高電平，並且 FA 操作的結果理論上位於 D 總線上，由於 LD_FA 需要額外的 CP）。如果我們想減 1，我們可以用類似的方式完成，但使用 ADD_FF（-1）代替。這會導致 CPU 速度變慢，但目標是建立一個能工作的系統，而不是一個速度快的系統。

CPU 閒聊

下面我將討論如何設計 CPU。即使這些圖可能不相關，我將使用當前的圖，一些圖我確實計劃更改。這些閒聊不會非常準確，只是對我的瑞典語書籍的翻譯，因此可能具有一些基本的理論用途。

架構閒聊

當研究更簡單的架構時，你發現 E 時鐘的產生是錯誤的。它應該只延遲到足以使資料在記憶體被定址時在資料匯流排（或輸出）處有效（這稱為訪問時間）。當你看 74HC 的速度有多快時，連續四個反相器（典型的 tpd 為 80ns）不足以使用舊的記憶體（典型的 27C256-15 EPROM 為 150ns）。解決方案可以是：讓 E 時鐘成為 CP 時鐘的（對稱）反相，這使得所選 EPROM 的最大頻率為 3MHz，或者我們可以讓 E 時鐘由外部產生。

這裡我補充說明一下，Spartan CPU 的最大頻率取決於全加器（FA）的設計方式。如果使用不帶進位加速且只有 8 位資料的全加器，則 FA 的傳播延遲（tpd）將為 16*tpd，而 Spartan 的 tpd 僅為 4ns。因此，如果我們使用 CP 時鐘的反轉技巧作為 E 時鐘，則 CP 的週期時間必須是兩倍，這意味著 32tpd，得出最大 CP 時鐘頻率為 1/(32*4ns)=8MHz。現在我看到，選擇的 EPROM 會進一步限制它，降至 3MHz (1/2x150ns)。然而，這主要與外部指令暫存器（6 個 27C512）有關，該暫存器計劃整合到 Spartan 中。雖然外部程式儲存器的預留型別相同，但最大 CP 為 3MHz。結論是，如果我使用最快的儲存器，最大頻率仍然只有 8MHz（我在資料手冊中看到 27C512 實際上可以製造到 100ns，但我相信還有更快的版本）。

條件碼暫存器（CCR）指示算術運算的結果。它使用稱為標誌的訊號來指示結果是否為零（Z=1）、負數（N=1）、過大（C=1）或溢位（V=1），其中 V 標誌是最神秘的，它處理運算元可能都為正但結果仍然為負（由於補碼）的特殊情況。例如，想象一個位元組的數字範圍是 -128 到 +127。如果將 30 加到 100，就會導致溢位。一開始我很難理解補碼，但現在我覺得它很簡單。例如，NEGA 指令將累加器中的數字取反並加 1，這給了我們補碼。除了溢位之外，該數字將以正數和負數形式都正確顯示。該數字的值僅取決於你如何看待它。例如，將 2 (0010) 與 C (1100) 相加，C 為 -4 或 12。結果是 E，它為 -2 或 14。

我還使用一個 H 標誌，但它不是真正的半進位標誌（可能被稱為“半位元組標誌”），而是用於嗅探分支偏移的極性（它總是注入到 FA 的頂部），因此 H 是偏移的第 7 位（或 a7），它告訴我們是否應該增加（a7=0）或減少（a7=1）程式計數器（PC）的高位元組。增加是透過將 PCHB 放在 FA 的頂部並新增 00h (ADD_00) 以及進位（來自之前的 LB+偏移加法）來完成的。這裡 a7=0 表示正偏移。如果 a7 被置位（偏移為負），我們將 PCHB 與進位和 FFh (ADD_FF) 相加，使 PCHB 減少一步。

我不知道這是否有效，但我們可以看看幾個例子（只使用 4 位）：如果偏移量為 3，輸入 LB (LB') 為 6，透過簡單的加法得到新的 LB 為 9（或 -7），這裡 a3=0，所以這是一個正加法，新的 HB 則為 HB+C+00（其中 C 來自 LB 與偏移的加法）。如果我們有 PC'=0010 0110 (HBLB) 並且 LB' 與 3 相加，LB 就會變成 1001。這裡沒有進位（<15），所以 PC 應該變成 0010 1001。然後我們有 PC'=26h 和 PC=29h，因此 +3 是由於偏移！如果偏移量為 8（或 -8），LB' 為 2，LB 就會變成 10（或 -6），這裡 a3=1，所以這是一個負加法，HB' 必須減少，新的 HB 為 HB+C+FF，使 HB' 減少一步（例如，從 2 減少到 1）。在我看來，當 a3 為高時，HB 總是減少一步，但是假設你有 PC'=0010 0010 (HBLB) 並且偏移量為 1000，偏移量 + LB 將為 1010 (-6)，如果我們現在減少（C=0）HB，我們最終會得到 0001，所以新的 HBLB 將變為 PC=0001 1010，而我們已經減去了 6。原始的 HBLB 為 22h (34)，新的 HBLB 為 1Ah (26)，差值 34-26 實際上是 8！然而，我對進位（C）的使用有點不確定，但如果你想新增兩個數字，進位總是必須存在，例如，將 Fh 與 2h 相加將得到結果 1 + 進位，其中進位需要處理。

堆疊指標暫存器（SP）是一個可並行載入的向上/向下計數器。它在復位/上電覆位時被預初始化為 00FF。在使用子程式（JSR）和堆疊操作（PSHA）時，使用它。它等待某種推送/彈出指令，例如 JSR（跳轉到子程式），該指令最初將低位元組（PC_LB）返回地址儲存在地址 00FF 上，將 PC_HB 儲存在 00FE 上。

累加器（SR_R+SR_L 或 AC）由兩個可並行載入的移位暫存器組成。它被分成兩部分，以便能夠向右移位（除以 2 的倍數）和向左移位（乘以 2 的倍數）。真正的累加器還應該能夠 INC/DEC，這表示向上/向下計數功能。然而，我們使用全加器（FA）而不是它來解決 INC/DEC。由於需要雙向移位，因此在（我的世界中）累加器必須由兩個獨立的移位暫存器組成。它已經實現了記憶體功能（L/R'+LD_D）來記住使用哪個單元。可能存在可以雙向移位的移位暫存器，但我還沒有找到任何。最後，我認為累加器值的移位並不重要，因為“精度”很差，我只想要我 LSHR/LSHL 指令中的功能。在 STA 訊號的幫助下，累加器值被放到內部資料匯流排（D）上，在 ALU 訊號的幫助下，該值被放到 ALU 匯流排（A）上。因此，所有算術和邏輯（AND、OR、XOR）運算都有一個由累加器控制的專用內部匯流排。INV（或 NOT）邏輯函式被硬連線到全加器（FA）。

程式計數器（PC）由一個可並行載入的向上計數器組成。它專門針對新 PC 地址的 HB（高位元組）和 LB（低位元組）設定了兩個獨立的載入暫存器。它還有兩個輸出三態緩衝器，將選定的 PC 位元組放到內部 D 匯流排（當 D 匯流排用於其他用途時，它們必須處於三態）上，該匯流排用於計算分支跳轉，例如 BEQ。PC 之後是地址暫存器（AR），它也由兩個位元組組成。這些暫存器可以分別使用 HB 和 LB 載入（因為我們使用的是非對稱架構）。還有一個控制訊號（EXT，表示擴充套件），這意味著地址匯流排（AB）可以暫時由指令（例如 STA $AAFF，表示將累加器 A 中的值儲存在 RAM（或 I/O）的該地址上）接管，並在之後將地址匯流排的控制權返回給 CP。

資料匯流排（DB）不包含暫存器。這是因為我認為不需要它，而且它甚至會破壞資料流，因為資料仍然只有在 t_acc（訪問時間）之後才能使用，即在記憶體被定址之後，也稱為 DAV（表示資料有效）。一個暫存器將意味著需要等待另一個時鐘週期。現在想象記憶體被定址，並且記憶體地址在 CP（時鐘脈衝）的正邊沿被輸出，同時我們有一個指令暫存器（IR）在 E 時鐘（它應該是其正邊沿延遲至少 t_acc 或 CP/2 的時鐘，在我的情況下）下工作。在 E 時鐘下，我們就可以安全地讀取資料（只要 CP/2>t_acc）。例如，PC 首先被加 1，然後 AR 被載入新的地址（延遲一個時鐘週期），並且記憶體被定址。在這個 CP 沿上，有一個 t_acc 的延遲，然後是 DAV，但在這裡，指令暫存器的 E 時鐘會在 CP/2 之前等待，然後讀取資料值。

指令暫存器（IR）由四部分組成。它們是兩個可並行載入的暫存器（IRR+BR）、一個計數器（IRC）和一個 ROM 記憶體，其中選定的指令以微指令的形式實現。所有指令以操作碼的形式進入指令暫存器暫存器（IRR），它始終識別這些指令。人們可能想知道為什麼，但它僅僅與馮·諾依曼機的開始有關（即按順序執行指令的機器），其中復位必須成功，並且程式儲存器中的操作碼必須與 IR 中的操作碼列表匹配，除此之外，你必須使用正確的運算元數量來為操作碼程式設計。我們的處理器使用三種運算元數量，分別是 0、1 和 2。操作碼 + 運算元構成一條指令。然後，操作碼是指令暫存器（IR）地址的一部分，在本例中是 ROM 的高位元組。在分支指令（由分支作為微程式碼執行）時，N 和 Z 標誌被載入到分支暫存器（BR）中，這成為 IR 地址的下一部分。由於我們的解決方法，這些輸入在復位後將保證為零，然後在 IR 檢測到分支時從 NZ 標誌獲取其值。在分支完成後，NZ 標誌會被複位（由就緒作為微程式碼執行）。這樣，BR 預設為 00。現在，如果有分支，NZ 的四種組合都是可能的，我們需要處理所有這些組合，除了 NZ=11 不能發生，因為一個數字不可能既為負又為零（也許這也要處理？）。指令暫存器計數器（IRC）有 16 個步驟。它透過在不同的訊號（如上圖中的 LDA）中抖動來依次遍歷順序微指令。所有這些都（初步）被程式設計到 6 個 EPROM（這裡稱為 ROM）中。據我所知，這些 EPROM 可以在我的 Spartan FPGA 中實現，這也是我的計劃，但我會逐步進行。

微指令漫談

這裡，一直在鬥爭，可能離正確很遠。然而，在嘗試進行微程式設計時，你最突出的感受是指令深度變得很大，這意味著所有指令都需要比 HCS08 多得多的時鐘週期。例如，EOR $ 需要十五個時鐘週期，而 HCS08 在四個時鐘週期內完成。我們在 3 個時鐘週期內完成 NEGA，而 HCS08 只需要 1 個時鐘週期，等等。所以，我們正在構建一個慢速處理器。但感覺它應該能夠執行並完成我們想要做的事情。總的來說，作者希望我們能夠在 CPLD 中程式設計這些微指令，這樣我們就不需要外部的 41 位記憶體。當我們決定構建一些有用的東西時，複雜度飛速上升，真是太可怕了。

作者再次擔心的是時序。我們無法充分控制取指令到達時會發生什麼。就目前而言，始終執行的微指令 AR，它更新地址暫存器，應該將 PC 移動到下一條指令，同時允許讀取該指令。但是時鐘呢？如果 Ready 完成了指令的執行，它也可以用來載入下一條指令（因為如果我們正確地執行，當 Ready 到達時，總會有一條新的指令在等待）？我們有一個同步，其中 E 時鐘在 CP 的中間變為高電平，這似乎給了我們一個很好的功能，我們可以同時做兩件事，因為我們可以同時使 OE 啟用並時鍾輸入結果，因為 OE 有時間在 CP 經過半個時鐘週期後輸出其訊號。然而，作者對此非常不確定。

加速處理器的其中一種方法是新增一個臨時暫存器，它只用於內部，並且可以在 ALU 匯流排和 D 匯流排輸出資料。一個問題是，在我們獲取到兩個位元組（例如，在 ORA $ 指令中）之前，我們不能更改地址暫存器（AR）。因此，我們必須將 HB 儲存在 A 中，這導致 A 必須在儲存之前被推到堆疊上，然後在我們獲取到值並可以執行操作時再拉回來。使用臨時暫存器，我們可以將處理器的速度至少提高 30%。另一種加速處理器的辦法是，透過引入幾個三態暫存器，使處理器能夠到達加法器（FA）的“頂部”。始終透過 FA 也給了我們一個額外的功能，即所有數字都可以進行 CCR 檢查（Z=1 表示零，等等）。

分支的實現有點特殊。當四個選定的分支操作碼中的任何一個被載入到指令暫存器 (IR) 中時，標誌 N 和 Z 將始終在 Branch 變為高電平的同時立即被載入。因此，我們似乎有四種不同的狀態需要解碼。但是，NZ=11 是無效的，因為 N 作用於 b7，而 Z 是所有位上的 NOR，所以該數字不能同時為負數和零，這就是為什麼 NZ=11 被排除在外的原因。我們剩下 NZ=00、01 和 10。NZ=00 表示該數字不是負數且不為零，即 >0。NZ=01 表示該數字為零，而 NZ=10 表示該數字 <0。例如，對於 BPL，我們應該在 NZ 為 00 時執行分支，但在另外兩種情況下退出並生成 Ready。但是，對於 BNE，我們必須對兩種組合（00 和 10）執行分支，只在 01 時退出。

我們現在將嘗試解釋一些註釋。AR 表示，如前所述，地址暫存器被更新（使用 LD_AR_HB 和 LD_AR_LB）。在從擴充套件定址 (EXT) 或步進 PC (EN_PC) 切換時，必須始終執行此操作。我們假設操作碼已正確載入，因此我們始終（除了在固有情況下）需要向前一步到第一個運算元（PC+1，AR）。我們想澄清一下，我們的程式計數器 (PC) 每次只步進一個位元組，根據上面的記憶體配置，我們約定最高地址向下。因此，PC 始終從低地址開始，在圖中向下步進（儘管我們始終向上計數）。復位後，它從第一個操作碼開始，在最極端的情況下，它需要再步進兩個位元組才能讀取所有運算元。PROM 中的儲存，根據 PC 的步進方向，是操作碼（1 位元組）、運算元 1（1 位元組）和運算元 2（1 位元組），其中運算元 1 始終是高位元組 (HB)，運算元 2 是低位元組 (LB)。當從外部進行分配時，它用右箭頭表示。內部分配，如累加器中的儲存，始終用左箭頭表示。資料匯流排上可能存在的任何東西都標記為 M（表示記憶體）。

乘/除雜談

我沒有在硬體上實現乘法 (MUL) 或除法 (DIV) 指令，因此我的 CPU 只能使用二進位制補碼進行加減運算。我選擇不這樣做，因為這相當複雜。真正的 CPU 確實必須實現這些指令，而我對此思考了很久。現在我認為可能可以用另一種方式來實現。

考慮一下，一個以指數形式表示的數字可以透過只加指數來進行乘法，對於除法，你只需減去指數。因此，如果這個數字可以用指數形式表示，那麼 MUL/DIV 就很容易實現。

我也有這樣的想法，我的 8 位只能表示大約 +/-128，但是如果位元組用指數形式表示，那麼可以表示像 +/-E38 這樣大的數字。我的想法（不使用尾數）的問題是解析度，因為每個相鄰數字將相差 2 倍，而我的表示方式計劃為

$Number=m\cdot 10^{e}=2^{bin}$

也就是說，在 CPU 中沒有尾數。

如果 bin 為 128，則該數字大約為 E38，但下一個較小的數字是它的二分之一 (bin-1)。

我計算出這可能有用，因為假設你想要表示 3，最接近的 2^bin 值是 4 (bin=2) 或 2 (bin=1)，併產生以下差異

$4/3=+33\%$

或

$2/3=-33\%$

如果我們想要表示 48（介於 64 和 32 之間），最接近的 bin 值是 6 或 5，因此差異仍然是 +33%/-33% 作為最大值。

對於涉及非常大或非常小的數字的物理學來說，這非常有效。例如，我經常加減指數並將數字四捨五入到半個數量級（3.16），因此 +/-33% 接近我認為必要的精度（只要不涉及私人的經濟學）。

問題是如何在將數字放入 CPU 之前對其進行轉換。這必須手動完成才能獲得某種精度。我的第一個公式

$Number=m\cdot 10^{e}=2^{bin}$

可以重新排列為

$binlg(2)=e+lg(m)$

或

$bin={\frac {e+lg(m)}{lg(2)}}$

這意味著要放入 CPU 的 bin 值是顯示的那個，然後 MUL 透過簡單的加法完成，DIV 透過簡單的減法完成，這樣 MUL/DIV 就不用硬體實現，至少這是我的想法。

當然，輸出也必須轉換，但你只需將輸出從 2 提高到獲得數字。

在 CPU 中使用一個普通的 8 位數字，可以透過簡單的移位來進行乘法和除法。在這種情況下，8 位數字僅在 +128/-128 範圍內。

左移一位表示乘以 2，右移一位表示除以 2，每次移位表示 2 的冪，因此左移兩位表示乘以 4，等等。

雖然只使用 8 位的數字範圍很小，但在實用性方面，這相當學術。

不過，最糟糕的情況是，假設你想要用 3 進行 MUL/DIV，而最接近的可能性是 4 或 2，那麼最大差異就是 +/-33%。

我得出的結論是，我的想法根本行不通。如果我們忽略數量級的尾數，那麼數字的指數將必須乘以 1/log2（3.32），而這個數字無法透過移位來實現（你只能得到 2 或 4）。使用線性表示（沒有二進位制尾數），你無法比 3 更接近，而當我們談論指數時，差異太大了。

我們可以看一個例子，假設第一個數字是

$10^{11}$

而另一個數字是

$10^{15}$

我們希望將它們相乘。

用紙筆很簡單，因為結果就是簡單地加指數，比如

$10^{11+15}=10^{26}$

但是，如果我們希望用 CPU 將它們轉換為二進位制形式，CPU 必須首先將指數乘以 3.32，而這無法實現，最接近的是 4（左移兩位），因此如果我們現在將 44 加上 60，我們將得到

$2^{104}$

這大約等於 E31，比它高 10000 倍（這個值也必須在輸出時轉換為十進位制形式）。

如果我們使用我的方法，我們可以線性地設定二進位制指數（但不包含小數），3,32 * 11 = 37 和 3,32 * 15 = 50，所以這個數字近似為

$2^{37+50}=1,5*10^{26}$

這個數字相當接近，但計算二進位制指數意味著將十進位制指數乘以 3,32，而我目前使用的 CPU 只能手動完成這個操作，3,32 只能透過移位來計算，但這顯然會導致很大的偏差。

所以這種方法行不通。

另一方面，如果你看一個 8 位 CPU，如果兩個運算元相等（操作是無符號的），它能處理多大數字？

256 的平方根只有 16。

因此，運算元的值（通常）必須很小，比如 16，對於 CPU 來說沒什麼用。

所以我得出結論，MUL/DIV 指令是沒必要的。

此外，CPU 最重要的指令是 ADD/SUB，因為這些指令是 CPU 依賴的指令，比如為 PC 跳轉新增分支偏移量等等。

我認為（觀察到）即使沒有 MUL/DIV，CPU 也能做很多事情。

我決定繼續我的想法，公式在這裡重複一遍

$m10^{e}=2^{bin}$

這意味著

$bin=(lg(m)+e)*3,32$

一個 MUL（微型）指令可能看起來像這樣（使用兩個累加器，我沒有，也不會有）

1) LDA #bin_1

2) LDB #bin_2

3) ADD (B+A->A)

4) STA $[bin_1+bin_2]（儲存指數和的地址）

5) LSRA #2（將 A 右移兩位，從而除以 4 而不是 3,32，得到 e'）

6) STA $[e']（e' 輸出，如 10^e'）

第 4 點不能完全實現，因為 bin 是線性的，沒有小數，最大的偏差是

${\sqrt {2}}$

對於要相乘的每個數字，對於兩個數字，偏差可能高達 2，但這是最壞的情況。偏差的計算方法是

${\frac {2^{4}}{2^{3,5}}}$

並且總是會差 2 的平方根，但這兩個數字必須都離整數 1/2，才能出現這種“災難”，你可以計算機率，因為每個數字都有三種可能的值（低、中、高），所以機率是 1/9，也就是大約 10%，但最壞情況下，兩個數字相乘時的偏差是 2，所以 4 點能提供最佳容忍度（如果值是手動轉換的）。

在第 5 點，我只是右移兩位，除以 4（應該除以 3,32），得到 e，並將 m 設定為 1，這會導致 1,6 的額外偏差，比如

$2^{4-3,32}$

所以輸出最多會偏離正確值 3,2（2 * 1,6），我用半個十年（3,16）作為計數單位，所以這不像看起來那麼糟糕。

為了簡單起見，我建議將 bin 值乘以 4 後放入 CPU，這樣從一開始就會有額外的偏差，但使用計算器來計算要相乘的數字的步驟使得這個想法變得毫無意義，因為用紙筆更容易完成。一個完整的指數乘以 4 很容易放入 CPU。

除了第 5 點，我認為偏差會變成

$({\sqrt {2}}\cdot 2^{4-3.32})^{2}=5,1$

所以最好在將 bin 值放入 CPU 之前使用計算器，但請記住，2 是最壞的情況，如果數字更匹配，偏差只有 2,6，而且我的最大偏差只有 10% 的風險。

然而，這是在“移位生成”輸出之前，如果它沒有手動完成，就會產生額外的 1,6 的偏差。

我也想擁有 DIV（除法）指令，這裡我需要減去指數，而我現在唯一能做到這一點的方法是使用二進位制補碼。這意味著 MUL 也必須使用二進位制補碼。我現在還不確定如何做到這一點。我在課程資料中看到浮點數實際上使用單獨的符號位表示，但我的計劃是使用二進位制補碼，具體方法我不確定。

由於我無法使用微編碼來程式設計值，MUL 將必須是一個單獨的程式。此外，如果 CPU 需要中繼結果，結果必須以二進位制程式碼形式給出。

例如，如果你想稍後新增結果，結果必須以二進位制程式碼形式給出（在 CPU 範圍內）。

所以，如果我們將 CPU 內的值定義為“CPU”，將 ADD 值定義為“bin”，同時我們想要相乘，從而新增指數，我們可以寫成

$bin=2^{CPU}$

這裡我們有加值（bin）的表示形式是 2^CPU，這意味著 CPU 儲存著指數版本，而我使用 8 位，CPU 值最多可以是 8（n）。

現在，如果我們透過新增兩個 CPU 指數來相乘兩個數字，我們可以說這個新數字是 CPU'，所以現在 bin' = 2^CPU'

這裡我們需要建立一個表，CPU' 不能大於 8，我們只能表示線性 n，所以我們需要將中間值設定為沒有小數的 n，比如 [0;1] = 0，[>1;2] = 1 等等，這種情況下最大的偏差是 2。

輸入時也會發生同樣的情況，CPU 只能有整數值。在輸入時，CPU 可以定義為

$lg(bin)=CPUlg(2)$

或

$CPU={\frac {lg(bin)}{lg(2)}}$

我們需要一個lg(bin)的表格，但是我的CPU無法進行計算。

所以我們需要兩個表格，例如：

$2^{CPU}$

和預備的：

$lg(bin)$

實際上，如果你使用：

$lg_{2}=3,32lg_{10}$

就可以消除lg2，從而可以寫成：

$CPU=lg_{2}(bin)$

所以我們需要一個lg_2(bin)的表格，其中bin小於255。

一個這樣的程式看起來像是：

MUL(bin_1, bin_2)

CPU=lg2(bin) [需要表格]

ADD CPU(bin_1, bin_2)

Bin=2^CPU [需要表格]

這可以在CPU中進一步傳遞，因為它是純HEX程式碼，這意味著結果可以稍後使用。

然而，我的最初想法是將一個10進位制指數數字替換為一個2進位制指數數字（其中2進位制數字缺少尾數）。在這裡，我們可以透過簡單地將指數相加來將兩個2進位制數字相乘。此外，可以表示相當大的數字（~E38）。對於加法，我們只需使用具有最大指數的數字（並跳過另一個）。

為了能夠在CPU內部傳遞一個數字，它必須是純8位HEX型別，而且不可能用二進位制程式碼寫出E38，所以這個值無法在CPU外部顯示。

如果我們堅持使用“128”，我們就可以操作它並將其呈現給外部世界，唯一的問題是這個數字不能大於128。

雖然我們可以在CPU內部正式表示E38，但我們不能在CPU外部使用它，但只要我們將其保持在CPU內部，它就可以工作，但在外部它只能表示為指數。

我得出的結論是，DIV不能用我的想法實現。原因是我只能使用二進位制補碼進行減法，而這根本行不通。我正在考慮浮點數的結構，它似乎有一個符號位，而其餘部分始終是一個正數。這對於MUL來說很好，因為指數只需要相加，但是對於DIV來說，指數需要相減，而我無法對不是二進位制補碼的數字進行減法。

可能存在一種解決方法，可以將無符號數字轉換為二進位制補碼，但是當使用8位和7位時，它們是正數（使用浮點數），而二進位制補碼的數字表示範圍僅在+/-64左右。

這是因為我們有一個符號位（b7），它給出其餘部分的二進位制補碼為+/-64。

我不知道如何或是否可以將正數轉換為二進位制補碼，除了如果b6=1，則該數字為負數，所以要使用的數字是該數字的反轉+1嗎？

此外，對於MUL和DIV，我都需要使用表格來轉換

$bin=2^{CPU}$

和

$CPU=lg_{2}(bin)$

而且這些表格遠非精確的。

雖然我已經得出的結論是DIV不能使用二進位制補碼，但我決定使用相同的數字表示方法來進行MUL/DIV，即最初使用二進位制補碼，計算過程中使用符號大小，最後使用二進位制補碼作為輸出。

使用二進位制補碼錶示“bin”的原因是我的CPU在內部使用它，因此生成的數字可以在CPU內部稍後使用，另一個原因是我喜歡正數和負數。實際上，摩托羅拉似乎在其超級MC6809中使用硬體實現的MUL/DIV，僅使用無符號數字，所以在這個方面（僅限於此）我的版本更好。

以下是我的MUL（8位）演算法：

MUL(bin1, bin2)

b7=1=>NEG(bin)+1=abs, s=1 [8位]

b7=0=>bin=abs, s=0

s1 XOR s2=s [儲存]

s.abs=Number [符號大小，8位]

Number'=Number AND 7Fh [7位，<64]

CPU=lg2 Number' [表格，我們的指數]

ADD CPU(Number1', Number2') [指數相加]

abs=2^{ADD} [表格，我們的量級]

s=0=>out=abs [來自上面儲存的s]

s=1=>out=NEG(abs)+1

out=7位二進位制補碼

這種解決方案的缺點在於，它僅涵蓋+/-64的數字範圍（但我認為可以透過乘數來增加，但數字之間的步長將是乘數），部分原因是，雖然我的CPU無法正確計數，我必須使用表格，但精度很差。但是，我已經計算出最大誤差為2.8，這低於我在進行物理計算時允許的半個十年的3.16。

以下是我的DIV演算法：

DIV(bin1, bin2)

b7=1=>NEG(bin)+1=abs, s=1 [8位]

b7=0=>bin=abs, s=0

s1 XOR s2=s [儲存]

s.abs=Number [符號大小，8位]

Number'=Number AND 7Fh [7位，<64]

CPU=lg2 Number' [表格，我們的指數]

SUB CPU(Number1', Number2') [指數相減]

abs=2^{SUB} [表格，我們的量級]

s=0=>out=abs [來自上面儲存的s]

s=1=>out=NEG(abs)+1

out=7位二進位制補碼

以下是我的第一個表格（二進位制數字的2的對數）：

CPU=lg2 bin Table [7位]

bin=[(>0);1]->CPU=0

bin=[>1;2]->CPU=1

bin=[>2;4]->CPU=2

bin=[>4;8]->CPU=3

bin=[>8;16]->CPU=4

bin=[>16;32]->CPU=5

bin=[>32;64]->CPU=6 [2^6=64]

這裡的誤差為2，而CPU是指數，2^1=2，但這是一個最壞情況。

以下是我的第二個表格（CPU從2開始的bin）：

bin=2^{CPU} Table [7位]

CPU=0->bin=1

CPU=[>0;1]->bin=2

CPU=[>1;2]->bin=4

CPU=[>2;3]->bin=8

CPU=[>3;4]->bin=16

CPU=[>4;5]->bin=32

CPU=[>5;6]->bin=64

這裡的誤差顯然是2，當然這是最壞的情況。

因此，總最大誤差為4（而不是我之前計算的2.8）。但是，4並沒有比我允許的3.16大很多，所以我的想法仍然可以使用。

新想法

我認為我現在有了另一個更簡單的解決方案，關鍵是建立一個3.32(1/lg2)的因子，用於乘法和除法。二進位制指數必須除以3.32才能得到十進位制指數，十進位制指數必須乘以3.32才能得到二進位制指數。雖然這些是指數，但如果我們例如將數字左移兩次來進行四倍的乘法，那麼誤差會變得相當大。

那該怎麼辦呢？我們需要用大約3.32進行乘法和除法。我的朋友們，解決方案可能在於兩個外部模擬乘法器/除法器，這樣我們就不需要單獨的數字乘法器或除法器了！

我的I/O記憶體對映為16kB，我的計劃是僅使用此區域內的1個I/O地址，以便能夠輸入（鍵盤）和顯示（顯示）值，在同一個地址進行讀寫。

但是，如果我想實現這個新想法，我需要使用兩個額外的I/O地址（一個用於模擬乘法器，另一個用於模擬除法器），並且需要重新配置I/O晶片使能。如果你問我，這是一個相當不錯的想法，這裡有一個例子

$10^{x}=2^{e}$

這意味著

$x=e\cdot lg2$

其中

${\frac {1}{lg2}}=3,32$

唯一的問題是x將變成一個分數值（即不是整數），因此輸出x不是整數，而我們習慣讀取尾數乘以整數指數。但是x可以轉換為整數並得到一個尾數，但這意味著使用計算器。另一方面，保留在CPU內部的值可以傳遞給其他指令。我不知道我是否正確，我只是寫下了我的新想法。

另一個讓我印象深刻的是，例如，如果你將兩個無符號的半位元組數相乘，不同的數字必須在 16 的範圍內才能不溢位 256。但我可能在這裡理解錯誤了，實際上這些相當小的數字是一種解析度，比如 1/16-16/16，就像尾數在 0-1 的範圍內一樣，這種解析度是 6.25%，實際上並不算太糟糕，因為假設我們使用 5V ADC，6.25% 意味著 LSB 為 0.3V。我不知道我們是否可以這樣計算，但我認為在實際情況下，這種較差的解析度並不算太糟糕，並且系統將適應更大的值，即使存在更大的絕對誤差。

今天我突然想到了一件微不足道的事情，CPU 外部的值是十六進位制 (Hex)，對於正常使用來說，這與 CPU 內部 (CPU) 的值相同！我最終理解這一點的方式是，對程式儲存器進行程式設計意味著純粹的十六進位制程式碼，我們必須將十進位制數字轉換為二進位制程式碼。因此，我們在這裡不使用十進位制數字，來自鍵盤的外部數字 (觀察) 雖然是十進位制的，但我們在 CPU 工作時會將它們轉換。現在我的計劃是透過加減指數來實現乘除，所以我必須將上面的公式改為

$Hex=2^{CPU}$

雖然 Hex 只有 8 位，因此最大值為 256，但 CPU 必須具有最大值為 8 的值，這意味著 3 位，而 CPU 是線性二進位制程式碼。對於相同的二進位制“寬度”，Hex 使用所有 8 位，而 CPU 僅使用 8 位中的 3 位。雖然 CPU 是線性二進位制程式碼，每一步都是一個整數，但中間的值將不得不被四捨五入，但兩個值都可能在整數之間，無論如何，誤差不能超過

${\frac {2^{2}}{2^{1}}}$

也就是 2。我計劃使用外部模擬 2.32 乘除和對數/指數實現，這些實現將非常精確，因此這裡沒有額外的誤差。同時，這個誤差也是最壞的情況，因為看一個實際情況，比如 CPU 值在 1 和 2 之間，這個實際的最壞情況意味著這個值應該是 1.5，但碰巧是 1 或 2，現在這個實際的差異小於 sqrt(2)，但最好不要期望超過這個值。

我已經找到了一種方法可以進一步減小這個誤差（我得到了 4%），方法是在指數中注入尾數，比如

$Hex=2^{m/n+CPU}$

其中 m 是尾數，n 是尾數的二進位制寬度，產生 m/n 在 [0;1] 的範圍內。我最近發現，用數字的寬度相除實際上意味著將 m 右移 n 次。這裡我們只需要處理移位出去的位。讓我覺得有趣的一件事是，我們如何知道移位實際上給出了一個分數？但我認為我已經得出了結論，我們不知道，就像 LSB 不需要是權重 2^0 一樣，而這只是我們對數字的簡化檢視，2^0 可以很容易地是 2^10，但相對來說，它仍然是正確的，因為位不知道它們的值！

但是，我不會關心 sqrt(2) 的最大差異，因為這樣一切都變得更簡單。我堅持使用純指數形式，而我的計劃是將指數相加以進行乘法。在這裡，我想出了一個類似於

$CPU=3,32lgHex$

所以我的步驟是
Hex->D/A->模擬對數=>3.32lgHex->A/D->CPU
CPU/3.32->D/A->模擬指數=>10^(CPU/3.32)->A/D->Hex

在這裡，我必須將 CPU 的 A/D 限制為僅 3 位/8h，但 Hex 輸出的 A/D 可以具有完整的 8 位解析度。現在我可以使用僅指數（CPU）來乘除數字。然而，一切都從我的第一個假設改變了，現在我需要兩個模擬裝置來實現

$3,32lg(x)$

和

$10^{(y/3,32)}$

我非常確定增益部分可以用相同的模組實現。我計劃使用 LM13700，我手頭有一些，但我並沒有完全理解這個神奇的 OTA（輸出跨導放大器），但我已經用它設計了一個 RMS 電壓計。需要注意的是，對數和指數函式也可以用一個簡單的二極體來模擬。

最後，我當然可以在數字上實現 MUL/DIV，但經過認真研究，我並沒有完全理解它們，我遵循的原則是我不使用我不理解的小工具（因為調整將是無望的）。正如我所說，我也不理解 OTA，但我對模擬裝置更熟悉。

今天我醒悟了，雖然上面在理論上是可行的，但我認為在實踐中它行不通，因為存在幾個問題，如果我從 CPU 可以根據上面的方法從 Hex 中獲得一個正確的值（帶有容差）這一事實開始。因此，我們在這裡被一個值困住了，而 CPU 的表示是按位進行的，所以如何將一個數字轉換為位流？用紙筆很簡單，但自動呢？例如，看最高位，這個位被計算為儘可能精確地表示這個數字。在我的世界裡，你會從原始值中減去這個新的值，並逐位繼續這個過程。但最初的測試怎麼辦？這個測試不是數字的，而僅僅是原始值的截斷，同時估計 n_max。雖然我的原始 CPU 只能加減，但這聽起來相當不可能。另一個問題是，我真正想要的是二進位制補碼形式的數字，那麼真的存在能夠處理這種情況的 ADC 和 DAC 嗎？我知道我最喜歡的 ADC（TDA8703）可以，但偏置怎麼辦？我認為連線用於二進位制補碼的 ADC 必須具有等於轉換範圍一半的直流輸入偏置。對於 DAC，如果存在二進位制補碼 DAC，則模擬輸出值也必須等於轉換範圍的一半，這意味著輸出總是直流的。

專業 MUL/DIV 演算法

在這裡，我將嘗試解釋兩種分別用於 MUL 和 DIV 的演算法。這些演算法可以用於在 CPU 內部實現硬體 MUL/DIV，但我將嘗試建立一個“軟體”版本。這當然會使我們的 CPU MUL 和 DIV 比必要的速度慢，但它可能是實現它們的一種更具教育意義且更簡單的方法。

MUL（羅伯遜演算法）

我將用一個圖片示例來展示這一點，但這裡我只是隨意談談。

如果我們將一個數字稱為被乘數 (y)，另一個數字稱為乘數 (x)，那麼我們有

y=被乘數 <y0, y1, y2...yn>
x=乘數 <x0, x1, x2,...xn>

這裡 x 乘以 y，所以如果 x 為 0，則不新增任何內容，但如果 x 為 1，則新增整個被乘數。

我在我的《數字技術》書中發現了一種名為 Robertson 演算法的演算法，該演算法闡述了

$p^{0}=0$
$p^{i+1}=(p^{i}+y\cdot x_{n-i})2^{-1}$
$i=0,1,2...n-1$
$p=p^{n}-y\cdot x0$

其中 p 是部分積，最後一個是積。該演算法實際上使用二進位制補碼中的數字，n 然而不包括“符號位”，因此如果一個數字是 8 位二進位制補碼，n 是 7。

使用我書中的示例，我得到了一個解釋，如下所示（小數點左側表示符號）

1) p^0=0.0 (sign.2n)
2) 與 x(n)*y 相加（y 向左移位 n 次）
3) 取和
4) 向右移位一步，得到 p^1
5) 與 x(n-1)*y 相加
6) 取和
7) 向右移位一步，得到 p^2
8) 重複此操作直到最後一位 (p^n)，然後減去 y*x(0)

如果 n 為 4（兩個 4 位資料，不包括符號位），2n 將為 8 位，因此 p(0) 為 8 位長，我們需要將被乘數左移 4 位，並建立一個由乘數決定的值（乘以被乘數），即，如果乘數中的乘位為 0，則新增 0，但如果乘位為 1，則新增整個被乘數 (y)。然後位置 8 就很有意思了，因為如果乘數的符號位 (x(0)) 為 0，則該數字為正，我們只需將 0 新增到 p^4，但如果符號位為 1，則 y 在新增之前取反，從而產生二進位制補碼乘法。

在進一步研究 Robertson 演算法的過程中，我首先得出結論，負值並不必要，因為您可以自己識別它們，其次，如果我的資料匯流排是 8 位（並且我們使用無符號數），則結果將為 16 位型別。因此，雖然我只能處理 8 位，但被乘數和乘數必須分別最多為 4 位。現在，16 的值並不大，但通常情況下，透過使用尾數+指數，我們只需要將尾數相乘，而在實踐中，尾數是一個不超過 1 的小數，而 1/16 (0,063) 是一個相當好的步長近似值。雖然我的數字只是整數，但這種情況在我的情況下卻無法使用。

另一方面，我認為我在這裡錯了，雖然我們可以識別數字是負數還是正數（並進行轉換），但 CPU 本身卻無法識別，因此，如果 CPU 給出一個負值，並且該值隨後用於乘法，則 CPU 必須能夠處理負數。然而，摩托羅拉公司在其出色的 MC6809 中，僅為無符號數硬體實現了 MUL/DIV。因此，似乎僅使用無符號數是有道理的。二進位制補碼也存在一個問題，因為“數字”此時僅由 7 位表示，這使得兩個運算元都需要為 3.5 位。

我還得出結論，我無法用我當前的 CPU 實現 Roberson，因為我無法使用進位右移（或 1），只能移入 0。但是，我有一個鬆散的計劃來實現一些新的指令，我稱之為 CSRA（進位右移累加器 A），但我確實不想重新編譯我的 Spartan。雖然我不使用尾數，但這有點沒有意義，還是我錯了？

如果被乘數和乘數在理論上分別為 16（4 位），則積將為 256（8 位），那麼我們有一個最大為 256 的積。現在，我們想要達到的值大約為 1/h~E34，對於 E34，我們需要 113 位。因此，使用 4+4 位來達到 E34 是沒有意義的，唯一的方法是改為只將尾數相乘，然後將指數相加。這被稱為使用浮點數，但我不想實現它。

如果我不實現浮點數（或尾數+指數），那麼 MUL 對我來說就沒有什麼實際用途，DIV 可能也沒有，因為會有餘數需要處理，我想。然而，Robertson 演算法很有趣，我會盡力解釋它，並想出一種彙編程式（可能使用我沒有的指令）。

看看我的圖片，我們可以發現如何進行乘法，我也列出了我的方法。Robertson 演算法實際上也適用於二進位制補碼，但展示它需要做太多工作，所以我只展示了正數的 Roberson。正如我們在這裡已經看到的，存在一個“問題”，因為進位必須得到處理（而我只能移入 0）。然而，最左側的基本演算法非常有趣。唯一的問題是要新增四個（左移的）數字，但我不知道這有什麼大不了的。下面是一個偽彙編程式嘗試：我在這裡放棄了，因為我實際上需要將乘數的有效位與被乘數相乘，而我沒有實現 MUL。然而，移位部分不是問題，因為我可以移入 0（LSLA/LSRA）。

但也許
LDA $y [四位，從 I/O 載入]
STA $y_value [儲存 y 以供日後使用]
LDA $x [四位，從 I/O 載入]
AND #$01 [A<-A AND M]
STA $bit4，即 bit4 的地址
LDA $x
AND #$02
STA $bit3
LDA $x
AND #$04
STA $bit2
LDA $x
AND #$08
STA $bit1
LDA $bit4
CMP #$01
BEQ $04 (JMP 地址為兩個位元組)
JMP Next1 (在 BNE 處完成)
JSR $Add_x_with_y，A<-x+y，將和儲存在 $sum4 中
JMP Next2
Next1:JSR $Add_0_with_y，A<-0+y，將和儲存在 $sum4 中
Next2:LDA $bit3
CMP #$02
BEQ $04
JMP Next3
JSR $LSLA_y_and_add_with_$sum4，將和儲存在 $sum3 中
JMP Next4
Next3:JSR $LSLA_y_and_add_with_0，將和儲存在 $sum3 中（這裡對 y 進行了正式移位）
Next4:LDA $bit2

等等

這不是一個快速的“演算法”，但我可能會完成它。摩托羅拉在其 MC6809 的資料手冊中沒有說明需要多少個時鐘週期，但它一定超過了 8 個。我使用了 26(+12) 個指令，其中最快的約為 5 個時鐘週期。假設 32 個指令用於兩個無符號四位數，如果我們使用 1MHz，那麼大約需要 32*5*1us=160us。然而，不需要等待，就像 FA 操作一樣，因此只需要 160us，這並不算太糟糕。但是，我還沒有計算出不同子例程的速度，因此 160us 是低估了。

我現在發現，HCS08(MUL) 對於兩個 8 位數只需要 5 個時鐘週期。令人驚訝的是，MUL 是硬體實現的。

我做了一些更改，因為子例程中的 RTS 會使程式返回並執行下一個地址。因此，如果下一個地址意味著另一個條件，那麼也會執行該條件。換句話說，我們不能同時執行 y+x 和 y+0 的加法。

MUL（Booth 演算法）

Booth 演算法在硬體實現方面更流暢，因此我也研究了該演算法。我得出結論，我需要進行乘法和除法。雖然我只使用了一些 4 位解析度的整數，但我認為與不超過 16（無符號）的數字相乘似乎毫無意義，但請看您是如何例如繪製一個函式來了解它的形狀。我認為您很少用超過十的“x”來繪製，例如，如果您想繪製一個二極體函式到 200mA，除非我進行縮放，否則我無法處理它，但我也可以繪製到 2 或“16”。您只需進行縮放！因此，重點更多在於解析度，例如您需要多少個步長？16 個步長是一個相當好的近似值。我現在想在硬體中實現 Booth，也許還會建立一個新的 Mathlab :-D

另一個要建立的是函式的泰勒展開式，考慮到二階，您需要進行乘法和除法（用 2!），並且您通常在接近於零的某個點評估泰勒展開式。因此，這些數字並不大。

我將繼續我的 CPU 任務，主要測試我當前的指令，只有當我能夠使所有 33 個指令都能正常工作時，我才會在硬體中實現 MUL/DIV，而我之前用軟體實現它們的方法似乎不起作用（而且速度會很慢）。原因是我大約 10 年前編譯了我的 Spartan，除非遇到任何指令的故障，否則我不想重新編譯。

演算法是這樣的

$x_{5}=0$
$p^{(0)}=0$
$p^{(i+1)}=(p^{(i)}+y\cdot (x_{5-1}-x_{4-1}))2^{-1}$
$i=0,1,2,3$
$p=p^{(}4)+y\cdot (x1-x0)$

這兩個二進位制補碼數字都是 5 位。

加法器中的不同單元有五個訊號：進位輸入、進位輸出、x 輸入、y 輸入和和輸出。進位是一個鏈，貫穿每個單元，但 x、y 和和始終可以在本地訪問。我已經在上面的書中寫過全加器 (FA) 的工作原理。

DIV（Burk 演算法）

除法可以使用 Burk 演算法進行，其過程如下

$r^{(0)}=x$
$z_{i-1}=(r_{0}^{(i-1)}\oplus y_{0})'$
$r^{(i)}=2r^{(i-1)}+(1-2z_{i-1})y$
$i=1,2,3,4$
$q=z+2^{-4}-1=z+1/16-1$
$r=r^{(4)}\cdot 2^{-4}$

其中一個數字/被除數 (x) 可以定義為

x=qy+r

其中 y 是除數，q 是商，r 是餘數。

第一個餘數 r(0) 當然是完整的被除數 (x)，r_0 是餘數的符號位，z 有點特別，但它處理了這樣一個事實：如果前一個餘數為負，則餘數的後續近似值會使新的餘數變小（因為它減去了）。只要除數和餘數為正，z 就為低。z 的權重為 2^(-n)，因此對於 z0，權重為 1；對於 z1，權重為 2^(-1)，依此類推。別問我關於這個 : :)

我一直很難理解這一點，我現在仍然不明白。但我已經看到它有效。關鍵是要理解 r_0 是前一個餘數的符號。

在圖片底部，我展示了一種用順序硬體實現除法的方案（我從我的 Danielsson 數字技術書籍中複製了它，但我很難理解。然而，他似乎知道自己在做什麼，所以我認為這是解決除法問題的正確方案）。但我確實認為順序方案可能緊湊而簡潔，但會依賴於 CPU 時鐘。在我的例子中，我並沒有為高速 CPU 設計，我只想讓它工作，但我認為組合方案更好，因為這裡 CPU 時鐘不會限制速度，而是門的傳播延遲會限制速度。然而，這裡的問題是門的數量會增加。

MUL/DIV 實現

我的計劃是隻使用位元組（雖然我沒有 16 位索引暫存器）。這意味著兩個二進位制補碼數字的乘積必須小於 8 位作為結果。然後每個數字都是 4 位，而值部分可以說只有 +/-7，因為只有 3 位。然後將這些數字合併成一個 8 位數字，以便低半位元組表示例如被乘數的二進位制補碼，另一個半位元組則表示乘數。然後二進位制補碼積是 7 位寬。對於除法，我將使用相同的方法，使用一個半位元組顯示二進位制補碼餘數，使用另一個半位元組顯示二進位制補碼商。

我認為，+/-8 左右的值範圍並不像聽起來那麼糟糕，因為它意味著 1/8 的解析度，即 0.125，因此如果你想表示圓周率，例如，你可以設定為 3+1/8，這相當接近；如果你想表示 4,9，你可以設定為 4+7/8，這也相當接近。

我認為乘法的用途是利用直線的方程式來擊中“斜率”點。斜率來自導數，你需要用類似於

$y=y_{0}+k(x-x_{0})$

的導數來擊中該點，其中 k 是導數，這裡很明顯，如果你想擊中該點，你需要進行乘法運算。但我認為這可以進行縮放，這樣你就不需要任何大的（或小的）數字，因此 3 位可能就足夠了（除了解析度差的情況）。

我已經上傳了 MUL 和 DIV 的兩個組合實現。我仍然沒有完全理解它們的工作原理，只是從我的 Digitalteknik 書籍中複製了原理圖。我現在不明白的一件事是關於 Burk 的 x4+ 是什麼。被除數 x 在值方面只有 4 位，那麼其他位是什麼？也許你在其餘被除數 x/256 不存在時將它們設定為零。前四位表示 x/16 的數量，向右移四位得到 x/256。

我還得出了這樣的結論：這種方法需要相當多的門。每個 FA/FS 由五個以上門組成，而 FA/FS 的數量大約為 20 個。

我將定義一個 FA/FS 只是為了好玩，它是一個相當簡單而有效的模組。然而，在我的 CPU 中，我只設計了一個 FA（全加器），對於減法，我需要對數字進行反轉並加上 1 再進行加法運算。這可以透過使用輸入端的 XOR 門和將進位輸入設定為 1 的組合 FA/FS 單元更容易實現。

然而，所示的 MUL 和 DIV 的組合解決方案相當快。使用早期的順序解決方案，CPU 時鐘將決定在 MUL/DIV 完成之前等待多長時間，這裡我們只需要等待傳播延遲。但是，CPU 時鐘的週期必須大於傳播延遲。

我的方法將類似於一個位元組，如下所示

$x_{0}x_{1}x_{2}x_{3}y_{0}y_{1}y_{2}y_{3}$

對於乘法，x 是乘數，y 是被乘數；對於除法，x 是被除數，y 是除數，所有這些都是二進位制補碼。

乘法的結果將是

$p_{0}p_{1}p_{2}p_{3}p_{4}p_{5}p_{6}$

然而，它只有 7 位，但我計劃將 p0 複製到 b7。

除法的結果將是

$r_{0}r_{1}r_{2}r_{3}q_{0}q_{1}q_{2}q_{3}$

它是 8 位。

那麼問題是如何處理結果。

實際實現

在這裡，我設計了一個稱為 X 暫存器的預暫存器，這是因為結果需要一些（短暫的）時間才能有效，並且你必須保持輸入，直到你能讀取結果。此外，輸入是兩個 8 位暫存器，它們只能按順序載入。

對於乘積 (p)，我將 p6 和 p7 縮短，以保持值對於正常的（8 位）取反完整；對於其餘部分 (r) 和商 (q)，我將它們合併成一個位元組，並將其餘部分作為高 nibble，這是因為我們主要對商感興趣，我們對結果位元組進行 AND 0Fh 操作。因此，其餘部分很特殊，因為它實際上有一個值為 1/64 的值，而商為 1/8。

可以在結果上執行 AND F0h 來獲取其餘部分，也許可以將它向右移四位以獲得正確的值。我認為 4 位數的值部分（3 位）然後被縮放為 1/8。我對這一點非常不確定，但只要我們專注於商，就不會有問題。無論如何，其餘部分都在那裡。

如你所見，此解決方案需要 6 個額外的控制訊號。現在我在我的原始 CPU 中使用 43 個控制訊號。43+6=49，這超出了我的 6 個 27C512 EPROM 的處理能力，因此我思考了一段時間，我是否需要一個額外的 PROM（+ 8 個訊號）。但看起來我並不需要它，因為我可以跳過一個訊號（IE_D_FA）並使用 X 暫存器。目前，我設計了一個 8 位多路複用器，以使用儲存在 FA 暫存器（LD_FA）中的擴充套件地址 HB，選擇 A 匯流排（來自累加器）或 D 匯流排（來自記憶體）來“從上方”進入全加器 (FA)。對擴充套件操作碼進行微編碼意味著，在 PC 加 1 後，它將停留在地址（用於值）的高位元組 (HB) 上，並且需要將此 HB 儲存起來以備後用。到目前為止，我一直在使用 FA 暫存器來臨時儲存 HB。但是，這不是一個很好的解決方案，但我認為它可以工作。我認為一個更好的解決方案是使用我的新 X 暫存器。

但是，我將繼續使用這個舊的解決方案（IE_D_FA）來進行我的 CPU 任務，因為我不想重新編譯（除非出於其他原因必要）。好處是，當我實現 MUL/DIV 時，我可以省略多路複用器並使用我的 x 暫存器，因此我的 6 個 EPROM 就足夠了。

我正在瞄準 MUL/DIV 的組合解決方案，因為我最喜歡它們。下一步將是設計一個組合的 FA/FS，我會盡快做到這一點。主要是在除法器中需要 FA/FS，但我計劃在所有地方使用 FA/FS，因為這樣可以簡單地選擇一直需要什麼。如果你沒有看到你需要什麼型別，那就很尷尬了。使用組合的全加器 (FA) 和全減法器 (FS)，你只需在硬體中設定一個控制位。FA/FS 比單獨的 FA/FS 更復雜一些，但我認為這是值得的。

我決定 X 暫存器將從 D 匯流排進入。這是因為這些值是從記憶體中輸入的。使用所示的版本，我將不得不先載入累加器，然後才能將值放到 X 暫存器中。

我現在對此感到後悔，並將按照圖紙進行，因為我有點喜歡我的 A 匯流排。透過累加器來輸入 X 暫存器的值不會有什麼麻煩。

我的計劃是不使用超過 6 個 IR PROM，這意味著最多有 48 個數據引腳。現在我有 43 個引腳，上面的要求需要 6 個額外的引腳。因此，我將跳過讀取高位元組暫存器，只讀取低位元組暫存器。我認為這不是問題，因為我仍然可以充分利用一個額外的 8 位暫存器，我們可以稱之為 X 暫存器。

FA/FS 組合

使用此單元，我們可以對二進位制補碼數字進行加法和減法運算。上面的全加器 (FA) 再次使用，但不是反轉並加 1，我可以透過將 SUB 設定為高電平來做到這一點。關鍵是 XOR 門會反轉 y，並且進位輸入設定為 1（這意味著加 1）。因此，減法非常簡單。

我將在我的 MUL/DIV 實現中使用這種方法，也許我甚至會更改框圖（它已經缺少一個功能）。

體系結構缺陷

我得出的結論是，我的架構在處理 FA 時無法正常工作。問題似乎在於我有一個 H 標誌（它不是真正的 H 標誌），它嗅探來自頂部的運算元的符號位。我認為嗅探應該針對結果進行。也就是說，嗅探結果的 N 標誌更好。讓我們說明幾個例子，第一個是向下翻滾（對於分支來說，所有這些都特別關鍵）。

假設 PC 的值為 FE02 (HBLB)，偏移量為 -4，那麼我們從 LB 開始，像這樣：

LB + (-4) = LB + 12

02
+
12
或
0000 0010
+
1111 1100
=
1111 1110, FE [-2 (2-4=-2)]

因此新的 LB 是正確的，但 HB 中的 E 必須減少，並且我們沒有進位，那麼該怎麼做呢？我想到一個主意，如果結果的 b7 被設定（讀取 N 標誌），我們只需將 HB 加上 -1，這在偏移量僅為一個位元組大時是可能的，因此我們只需要將 HB 的最低有效位向下計數一步。換句話說，我只用 ADD_HB+ADD_FF+C 將 FF 新增到 HB 中（當 N 被設定時）（C 在這裡為零，但我認為我應該始終帶有進位進行加法）。

讓我們看一下向上翻滾，假設 HBLB 是 FDFE，而加的是 +4，那麼我們有：

FE
+
04
或
1111 1
1111 1110
+
0000 0100
=
0000 0010, 02+進位

這裡我們得到 02h，但帶有進位，這並不奇怪，因為它意味著溢位，並且 HB 的最低位必須增加，這裡我僅將 HB 加上進位 (ADD_HB+ADD_00+C)。到目前為止，我一直在嗅探我的特殊 H 標誌（上運算元的符號），但我將把它改為嗅探結果。

如果我們現在看一下我們的中間結果，我們會發現如果符號位 (b7, N 標誌) 被設定，我們應該加上 FF，如果沒有被設定，我們應該加上 00。

我的加法器存在重大問題。我得出的結論是，我的版本根本無法正常工作，我正在努力弄清楚如何修復它。僅僅檢視 N 標誌並不起作用。我還實現了一個 V 標誌，但我並不完全理解它（除了它嗅探兩個最新的進位，即輸出進位和之前的進位），但類似的東西可能有效。現在我認為 XOR 應該是一個反向 XOR，但我不知道。等我瞭解更多資訊後會再聯絡你。

我想我現在知道該怎麼做了，它比我想象的要簡單。如果偏移量為負 (a7=my H=1)，則將 FF (-1) 加到高位元組 (HB)，如果偏移量為正 (H=0)，則將 00 加到高位元組。請注意，您還必須將 HB 加上進位，對此我有點不確定，但如果您看一下，如果我們使用 16 位 FA，進位始終存在。因此我們需要處理進位以使其正確。

檢視我上面的解決方案，我唯一需要改變的是在兩種情況下都強制執行 ADC（帶進位加法）。這可以透過在嘗試更改 HB (ADD_HB) 時在控制訊號 ADC 旁邊放置一個 OR 門來實現。

現在，我仍然不想重新編譯（因為距離上次編譯已經很久了），這意味著我將不得不跳過所有四個分支，集中驗證其餘部分。只要沒有 HB 操作（即分支），我似乎能夠使用 FA 來進行 INCA/DECA（遞增/遞減），因為這些僅僅是 "LB" 操作。

也許我還沒有解決問題。如果您檢視我上面的 FA/FS 電路，減一意味著偏移量完全反轉，並且進位設定為高。我們希望將 HB 減一。那麼偏移量一應該僅反轉，並加上進位以使 HB 向下翻滾。如果我們加上 FF（和進位），我們加多了，可以這麼說。我現在認為我們應該加上 FE，因為這是一的反轉。然而，一個正常的數值將透過加上 FF 來遞減，但在這裡我們需要處理進位。

等等，在我上面的 FA/FS 中，進位被強制為減法的 1（偏移量僅反轉）。但如果我們跳過進位的強制設定，HB 應該加上 FF。然而，在這裡我們知道我們想要減法。我得再想想這件事。

我想我現在明白了。當偏移量的 a7 被設定時，你將 HB（PC 的 HB）加上偏移量的二進位制補碼。這意味著你只需將 ADD_FF 和 HB 以及進位一起執行。如果偏移量的 a7 為零，則將 ADD_00 和 HB 以及進位一起執行。因此，我唯一遺漏的是加上進位。在我上面的原理圖中，加上進位似乎不起作用，但我仍然可以將控制訊號 ADC 設定為 1 以加上前一個進位。因此，我不需要重新編譯，我仍然可以實現分支！

我將一步一步地進行，使用我當前的架構。雖然我使用 43 個控制訊號，我的 MUL/DIV 解決方案需要 6 個額外的控制訊號，但看起來我需要另一個 27C512。但是，當/如果我實現 MUL/DIV 時，我可以省略訊號 IE_D_FA，因為該訊號只是在那裡用於啟用 A 匯流排或 D 匯流排從上面進入 FA。雙匯流排在您臨時希望儲存例如 PC 的高位元組以進行分支跳轉時非常有用，並且沒有其他地方可以儲存 PCHB（它首先出現在程式記憶體中）。然而，如果我在 MUL/DIV 中實現一個 X 暫存器，我可以將 PCHB 儲存在那裡，而 IE_D_FA 就會變得過時。因此，我認為我會繼續使用僅 6 塊 27C512。

缺點是，如果我使用 IE_D_FA 對指令進行微編碼，那麼當/如果我決定實現 X 暫存器時，我將不得不重新程式設計微編碼，但我認為這不是什麼大問題，我更高興的是我找到了一個不用重新編譯就能實現分支的方法。

CPU 測試程式（偽彙編程式）

讓我們從程式設計 $8000 的復位向量開始，這是我們的程式開始的地方。因此，我們在 $FFFE 中程式設計 $80，在 $FFFF 中程式設計 $00。當為我們的 CPU 通電時，起始地址為 $FFFE，它儲存著 $80，然後讀取 $80，使用我們的 DC 時鐘 (SW2)，我們最終得到 $FFFF，並讀取 $00，這使得我們的起始地址變為 $8000。在這裡，第一個操作碼 (LDA 或 $A6) 被讀取，再次使用 SW2 使它的運算元 #$FE 被讀取。我認為我會省略所有立即數值之前的 # 符號，因為很明顯它是一個立即數值（僅一個位元組）。然而，$ 符號告訴我們該數值是十六進位制的。但我也在地址之前使用 $（它們也是十六進位制的），因此純 $ 可能適合擴充套件定址（RAM 或 I/O），而立即定址（屬於程式記憶體）之前的一個位元組的 $ 之前可能適合 #。

我們現在將嘗試編寫一個程式，根據上面 CPU 助記符一章中描述的 33 條指令進行測試，因此我們從起始地址 $8000 開始。然後，一個測試程式可能看起來像下面這樣，我們為所有指令添加了絕對地址，通常不會這樣做，因為程式可以放置在記憶體中的任何位置（並且由連結器完成，我認為）。由於教學原因，我們選擇了絕對地址。

我們的記憶體對映告訴我們，$4000 位於 I/O 區域內，因此我們可以對同一個地址進行讀寫。由於我們選擇的記憶體對映，不可能有滑鼠。

請注意，可以使用 HCS08 編譯器編寫更復雜的程式。

我的程式僅適用於 “DC 時鐘”，在實際情況下必須有迴圈，但我只想驗證指令（其中 LDS/NOTA 已被省略）。

$8000 LDA #$FE //-2
$8002 ADD #$02 //A 中的值現在為 $00，但已產生進位
$8004 ADC #$00 //帶有進位加法
$8006 STA $4000 //$01 在 I/O 輸出
$8009 LDA $4000 //用 HEX-sw 設定 $FE
$800C ADD $4000 //用 HEX-sw 設定 $02
$800F ADC $4000 //用 HEX-sw 設定 $00
$8012 STA $4000 //$01 在 I/O 輸出
$8015 LDA #$FE //-2
$8017 DECA //遞減一步
$8018 CMP #$FC
$801A BNE $FC //(-4)，這將執行兩次
$801C STA $4000 //$FC 在 I/O 輸出
$801F INCA //遞增一步
$8020 CMP $4000 //設定 $FF
$8023 BNE $FB //(-5)，這將執行兩次
$8025 CMP #$FF
$8027 BEQ $01 //下一條指令
$8029 LDA #$00
$802B CMP #$01
$802D BMI $01 //A-M<0，下一條指令
$802F LDA #$02
$8031 CMP #$01
$8033 BPL $01 //A-M>0，下一條指令
$8035 LDA #$01
$8037 EOR #$F0 //$01 XOR $F0=$F1
$8039 STA $4000 //$F1 在 I/O 輸出
$803C EOR $4000 //設定 $01
$803F STA $4000 //$F0 在 I/O 輸出
$8042 JSR $9000 //這是一個子程式
$8045 LDA #$02
$8047 LSRA
$8048 STA $4000 //$01 在 I/O 輸出
$804B LSLA
$804C STA $4000 //$02 在 I/O 輸出
$804F LDA #$01
$8051 NEGA
$8052 STA $4000 //$FF 在 I/O 輸出
$8055 NOP //無操作
$8056 LDA #$F2
$8058 ORA #$F3
$805A STA $4000 //$F3 在 I/O 輸出
$805D ORA $4000 //設定 $F4
$8060 STA $4000 //$F7 在輸出
$8063 PSHA
$8064 PULA
$8065 STA $4000 //$F7 再次在 I/O 輸出
$8068 SUB $4000 //設定 $FF
$806B STA $4000 //$F6 在 I/O 輸出
$806E SUB #$FF
$8070 STA $4000 //$F5 在 I/O 輸出
$8073 LDA #$01
$8075 ADD #$01 //沒有設定標誌
$8077 TPA //CCR->A
$8078 STA $4000 //C、V、Z、N 和 H 應該都為零（即 b7-b3），輸出為 $00
$807B LDA #$0F
$807D AND #$02
$807F STA $4000 //$02 在 I/O 輸出
$8082 AND $4000 //設定 $F2
$8085 STA $4000 //$02 在 I/O 輸出
$8088 JMP $8000 //從頭開始

$9000 RTS //在這個地址，我們暫時只編程 RTS 的操作碼，即子程式返回

$FFFE $80
$FFFF $00 //在這裡，我們程式設計重置向量，它指向程式開始的位置

我在這裡列出測試的指令
1) LDA #, $
2) ADD #, $
3) ADC #, $
4) STA
5) DECA
6) CMP #, $
7) BNE
8) INCA
9) BEQ
10) BMI
11) BPL
12) EOR #, $
13) JSR
14) LSRA
15) LSLA
16) NEGA
17) NOP
18) ORA #, $
19) PSHA
20) PULA
21) SUB #, $
22) TPA
23) AND #, $
24) JMP
25) RTS

這個列表有 25 條指令，但我還測試了立即數和擴充套件指令，因此實際測試指令的數量似乎為 33。我在上面的助記符對映中計算了 33 條指令。

CPU 測試程式（彙編程式）

在這裡，我們指定程式儲存器中每個地址的地址應該發生什麼。我們使用純十六進位制程式碼（不再使用 $ 符號），並省略助記符，但將其保留為註釋，以便跟蹤發生了什麼。我添加了如何使用十六進位制開關（或鍵盤）進行設定，以及在顯示屏上應該顯示什麼。這樣，該程式就可以打印出來，並在我們的 CPU 執行時檢視。

8000 A6 //LDA #
8001 FE
8002 AB //ADD #
8003 02
8004 A9 //ADC #
8005 00
8006 C7 //STA $, 01 輸出
8007 40
8008 00
8009 C6 //LDA $, 設定 FE
800A 40
800B 00
800C CB //ADD $, 設定 02
800D 40
800E 00
800F C9 //ADC $, 設定 00
8010 40
8011 00
8012 C7 //STA $, 01 輸出
8013 40
8014 00
8015 A6 //LDA #
8016 FE
8017 4A //DECA
8018 A1 //CMP #
8019 FC
801A 26 //BNE
801B FC //(-4)
801C C7 //STA $, 1C 輸出
801D 40
801E 00
801F 4C //INCA
8020 C1 //CMP $, 設定 FF
8021 40
8022 00
8023 26 //BNE
8024 FB //(-5)
8025 A1 CMP #
8026 FF
8027 27 //BEQ
8028 01
8029 A6 //LDA #
802A 00
802B A1 //CMP #
802C 01
802D 2B //BMI
802E 01
802F A6 //LDA #
8030 02
8031 A1 //CMP #
8032 01
8033 2A //BPL
8034 01
8035 A6 //LDA #
8036 01
8037 A8 //EOR #
8038 F0
8039 C7 //STA $, F1 輸出
803A 40
803B 00
803C C8 //EOR $, 設定 01
803D 40
803E 00
803F C7 //STA $, F0 輸出
8040 40
8041 00
8042 CD //JSR $
8043 90
8044 00
8045 A6 //LDA #
8046 02
8047 44 //LSRA
8048 C7 //STA $, 01 輸出
8049 40
804A 00
804B 48 //LSLA
804C C7 //STA $, 02 輸出
804D 40
804E 00
804F A6 //LDA #
8050 01
8051 40 //NEGA
8052 C7 //STA $, FF 輸出
8053 40
8054 00
8055 9D //NOP
8056 A6 //LDA #
8057 F2
8058 AA //ORA #
8059 F3
805A C7 //STA $, F3 輸出
805B 40
805C 00
805D CA //ORA $, 設定 F4
805E 40
805F 00
8060 C7 //STA $, F7 輸出
8061 40
8062 00
8063 87 //PSHA
8064 86 //PULA
8065 C7 //STA $, F7 輸出
8066 40
8067 00
8068 C0 //SUB $, 設定 FF
8069 40
806A 00
806B C7 //STA $, F6 輸出
806C 40
806D 00
806E A0 //SUB #
806F FF
8070 C7 //STA $, FE 輸出
8071 40
8072 00
8073 A6 //LDA #
8074 01
8075 AB //ADD #
8076 01
8077 85 //TPA
8078 C7 //STA $, 00 輸出
8079 40
807A 00
807B A6 //LDA #
807C 0F
807D A4 //AND #
807E 02
807F C7 //STA $, 02 輸出
8080 40
8081 00
8082 C4 //AND $, 設定 F2
8083 40
8084 00
8085 C7 //STA $, 02 輸出
8086 40
8087 00
8088 CC //JMP $
8089 80
808A 00

9000 81 //RTS

FFFE 80
FFFF 00

CPU 測試程式（可刻錄的純機器碼）

在這裡，我們列出了上述程式，以便 PROM 燒錄器可以使用。每行/地址包含 8 個位元組。

8000 A6 FE AB 02 A9 00 C7 40
8008 00 C6 40 00 CB 40 00 C9
8010 40 00 C7 40 00 A6 FE 4A
8018 A1 FC 26 FC C7 40 00 4C
8020 C1 40 00 26 FB A1 FF 27
8028 01 A6 00 A1 01 2B 01 A6
8030 02 A1 01 2A 01 A6 01 A8
8038 F0 C7 40 00 C8 40 00 C7
8040 40 00 CD 90 00 A6 02 44
8048 C7 40 00 48 C7 40 00 A6
8050 01 40 C7 40 00 9D A6 F2
8058 AA F3 C7 40 00 CA 40 00
8060 C7 40 00 87 86 C7 40 00
8068 C0 40 00 C7 40 00 A0 FF
8070 C7 40 00 A6 01 AB 01 85
8078 C7 40 00 A6 0F A4 02 C7
8080 40 00 C4 40 00 C7 40 00
8088 CC 80 00 FF FF FF FF FF

9000 81 FF FF FF FF FF FF FF

FFF8 FF FF FF FF FF FF 80 00

未程式設計地址中的資料通常為 FF。為了清晰起見，我添加了 FF 以使行看起來更好。

CPU 測試程式（s 記錄）

這裡我 Dataman S4 燒錄器的語法是
地址、校驗和、要刻錄的位元組
校驗和實際上很簡單，它似乎只是位元組的計數（包括校驗和）。在這裡，我列出了每行/地址 8 個位元組的資料，因此每行的校驗和相同，但在實踐中並非如此（見下文）。

S1 0B 80 00 A6 FE AB 02 A9 00 C7 40
S1 0B 80 08 00 C6 40 00 CB 40 00 C9
S1 0B 80 10 40 00 C7 40 00 A6 FE 4A
S1 0B 80 18 A1 FC 26 FC C7 40 00 4C
S1 0B 80 20 C1 40 00 26 FB A1 FF 27
S1 0B 80 28 01 A6 00 A1 01 2B 01 A6
S1 0B 80 30 02 A1 01 2A 01 A6 01 A8
S1 0B 80 38 F0 C7 40 00 C8 40 00 C7
S1 0B 80 40 40 00 CD 90 00 A6 02 44
S1 0B 80 48 C7 40 00 48 C7 40 00 A6
S1 0B 80 50 01 40 C7 40 00 9D A6 F2
S1 0B 80 58 AA F3 C7 40 00 CA 40 00
S1 0B 80 60 C7 40 00 87 86 C7 40 00
S1 0B 80 68 C0 40 00 C7 40 00 A0 FF
S1 0B 80 70 C7 40 00 A6 01 AB 01 85
S1 0B 80 78 C7 40 00 A6 0F A4 02 C7
S1 0B 80 80 40 00 C4 40 00 C7 40 00
S1 0B 80 88 CC 80 00 FF FF FF FF FF

S1 0B 90 00 81 FF FF FF FF FF FF FF

S1 0B FF F8 FF FF FF FF FF FF 80 00

CPU 測試程式（一次一條指令）

我希望一次測試一條指令，而不是多個 EPROM（或重新程式設計），我們可以使用一個 EPROM，但需要像這樣進行程式設計

LDA $I/O [將 I/O 地址輸入上的值載入到累加器 A 中，我將此行和地址定義為“開始”]

CMP $#00 [將該值與 00h 進行比較，需要將其設定為繼續]

BNE -6 [只要 I/O 不是 00h，它就會重複/等待，預計跳轉地址的 LB 將使其退出迴圈]

PSHA [跳轉地址的低位元組（LB）被壓入堆疊，以便稍後獲取]

LDA $I/O [設定 00h 以進行參考，否則該值為 LB]

CMP $#00 [檢查該值是否為 00h]

BNE -6 [當該值不為 00h 時，它會重複]

LDA $I/O [設定跳轉地址的 HB，I/O 現在處於 00h]

CMP $#00 [檢查該值是否為 00h]

BEQ -6 [當該值不為 00h 時，它將繼續執行並將儲存在 A 中的“正確”HB 用於跳轉地址]

PSHA [跳轉地址的高位元組（HB）被壓入堆疊]

RTS [從堆疊中拉出 HBLB，並使 PC=HBLB]

在子程式中，你只需使用 JMP $start 結束，然後重複所有操作。下次，你將輸入另一個 HBLB，程式計數器（PC）將跳到該地址，該地址是新子程式/程式的開頭。輸入正確的 HBLB 至關重要，因為否則我們將跳到沒有程式（因此沒有 JMP）的地址區域。但是，在這種情況下，我們只需開啟和關閉電源即可。

等待迴圈沒有必要，因為我們有一個以外部時鐘形式的“進入”。因此，外部值僅在按下回車鍵時才被鎖存到 CPU 中，然後 CPU 只要有時間就會讀取鎖存的值。但是，我將保留此程式，因為它很有趣，它說明了如何在外部 I/O 值的幫助下設定新的 CP 值。

另一個小問題是，我們需要在測試指令之前測試所有這裡使用的指令。因此，此程式被丟棄，我將使用盡可能少的指令的程式，從原始測試程式開始。

CPU 測試程式（原始）

在這裡，我列出了原始測試程式，其中至少 JMP 指令可以正常工作。

$9000 LDA$ //C6
$9003 CMP# //A1
$9005 BNE //26
$9007 STA$ //C7
$900A LDA$ //C6
$900D CMP# //A1
$900F BNE //26
$9011 STA$ //C7
$9014 JMP$ //CC

我只能在這裡猜測，因為我沒有完整的程式，但也許

$9000 LDA$ $4000，設定 $01 [測試資料匯流排的讀取部分]
$9003 CMP# $01 [測試全加器 FA 的減法部分]
$9005 BNE -6 或 $FA [測試分支是否有效，以及 PC 是否可以相應地更改]
$9007 STA $4000，$01 輸出 [測試地址匯流排的寫入部分]
$900A JMP $9000 [測試 PC 是否可以更改]

我在這裡對程式進行了簡化，旨在突出最重要的部分，S 記錄為

S1 06 90 00 C6 40 00
S1 06 90 03 A1 01 FF
S1 06 90 05 26 01 FF
S1 06 90 07 C7 40 00
S1 06 90 0A CC 40 00

微指令程式設計示例

為我們的 CPU 程式設計微指令的方式如下：如果我們檢視第一個 EPROM (M0) 以及僅 RST 指令，它可能會像這樣程式設計

0000 00
0001 00
0002 00
0003 00
0004 00
0005 00
0006 00
0007 01

或作為 S 記錄
S1 0B 00 00 00 00 00 00 00 00 00 01

為了比較，ADC# 可以像這樣程式設計
A900 00
A901 00
A902 00
A903 88
A904 00
A905 01

或作為 S 記錄
S1 09 A9 00 00 00 00 88 00 01

然後，IR EPROM 的程式設計可以壓縮為（程式設計兩個指令）
S1 0B 00 00 00 00 00 00 00 00 00 01
S1 09 A9 00 00 00 00 88 00 01

我不喜歡不同的校驗和，因此在實踐中，這會導致
S1 0B 00 00 00 00 00 00 00 00 00 01
S1 0B A9 00 00 00 00 88 00 01 FF FF

其中我用 FF 填充了最後兩個位元組（如同在未程式設計的單元格中）。

CPU 靈感

CPU（中央處理器）是計算機的大腦。然而，指令暫存器（IR）是 CPU 內部的“大腦”。沒有 IR（或圖中的 ROM），就不可能解釋或執行指令。指令也必須以預定義的形式出現，否則“大腦”會迷路。有趣的是，這裡實際上存在兩種“大腦”。也許你可以將 CPU 稱為“大腦”，將指令暫存器稱為“小腦”？

基本 CPU

這幅圖顯示了最簡單的機器，它可以代表一個非常簡單的 CPU（實際上是我的靈感來源，據說它代表一臺洗衣機），內部指令（操作碼或 OP-kod）在這裡得以實現。資料輸出實際上可以控制要做什麼以及按什麼順序。該機器使用分頁記憶體，這意味著每個操作碼或指令都被分配了一個特定的記憶體區域以供遍歷。這是因為計數器（Räknare）遍歷 IR 地址的低位。我在上面將這個計數器稱為 IRC，代表指令暫存器計數器。“Klar”表示準備就緒。

現代 CPU

這幅圖顯示了一個比較現代的 CPU 的架構。它包含一個用於算術和邏輯運算的單元，稱為 ALU（算術邏輯單元），一個累加器（AC），一個程式計數器（PC），一個數據暫存器（DR），一個地址暫存器（AR）和一個指令暫存器（IR），以及一些控制訊號。

結語

以上是對理解和設計 CPU 的嘗試。並非總是能夠完全理解，因此我經常在嘗試理解的過程中偏離方向。隨著時間的推移，某些事情變得清晰起來，為本書提供了一些結構。就目前的感覺而言，存在很少的差異。現在存在的差異是那些考慮微指令編碼的差異。我認為第一次嘗試讓他們工作起來相當困難。

嘗試寫下我所知道、所思以及有時所相信的東西非常有趣。唯一有點令人悲傷的是所有這些閒聊，但我感覺我既沒有動力也沒有想要對此做些什麼。很大程度上是因為它是開發和自學的一部分。

來源

http://www.freescale.com/files/microcontrollers/doc/ref_manual/HCS08RMV1.pdf
Per-Erik Danielsson，Lennart Bengtsson，Digital Teknik，第三版，1986 年，瑞典
John P. Hayes，計算機體系結構與組織，第二版，1988 年，新加坡