元胞自動機/列出原像

本文描述了兩種用於列出當前配置的原像的演算法。第一個演算法在 Andrew Wuensche 的許多文字中都有描述，第二個演算法是本書中介紹的。

原像網路

為了便於根據圖中路徑描述反向演算法，引入了新的圖，即原像網路。

單個單元格的原像圖是該單元格的原像網路。就像序列中單元格的原像矩陣 $\alpha =c_{0},c_{1},\dots ,c_{x},\dots ,c_{l-1}$ 長度 $l$ 對齊成一條鏈並相乘，每個單元格的原像圖可以對齊形成原像網路。如果考慮了 De Bruijn 圖中的所有連結，那麼只有那些對映到觀察到的單元格的鄰域的連結才是有效連結。圖中節點之間的每個連結或路徑，由許多連結組成，都是一個區域性有效路徑。

元素 $d_{o_{L}o_{R}}$ 在相乘的原像矩陣 $D(\alpha )$ 中統計從左側重疊之一 $o_{L}=o_{0}$ 開始，並以右側重疊之一 $o_{L}=o_{l}$ 結束的原像數。同理，原像網路中兩個重疊之間有 $d_{o_{L}o_{R}}$ 條不同的有效路徑。

全域性有效的定義取決於有限格是有界還是迴圈。

在有界格上，全域性有效路徑連線左側邊界上的任何重疊到右側邊界上的任何重疊。
在迴圈格上，全域性有效路徑必須始於並止於相同的重疊值。

區域性有效路徑上的節點是區域性有效節點。全域性有效路徑上的節點是全域性有效節點。

指向連結以增加位置索引方向的箭頭可以省略。

連結權重

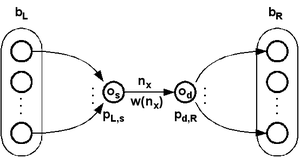
原像網路中的重疊和鄰域可以根據透過它們的全域性有效路徑的數量進行加權。權重可以在原像網路上以節點大小（在示例中未使用）和線粗細來表示。由於原像的數量可能呈指數級增長，因此粗細可能是權重的對數。

w_{log}=\log _{|S|}w

取決於有限格是有界還是迴圈，有兩種不同的方法來定義和計算權重。

有界格

連結 $n_{x}=o_{s}c_{s}=c_{d}o_{d}$ 在位置索引 $x$ 的權重是

從左邊界 $b_{L}$ 到源重疊 $o_{s}$ 的路徑數量 $p_{b_{L},o_{s}}$ 和
從排水重疊 $o_{d}$ 到右邊界 $b_{R}$ 的路徑數量 $p_{o_{d},b_{R}}$ 的乘積。

w(n_{x})=p_{b_{L},0_{s}}\cdot p_{o_{d},b_{R}}

乘積的兩個部分都包含在原像向量中，左側為 $b_{s}$ ，右側為 $b_{d}$ 。

b_{s}=b_{L,x}=b_{L}D(c_{0}c_{1}\dots c_{x-1})

b_{d}=b_{x+1,R}=D(c_{x+1}c_{x+2}\dots c_{l-1})b_{R}

迴圈格

在迴圈格上，連結 $n_{x}=o_{s}c_{s}=c_{d}o_{d}$ 在位置索引 $x$ 的權重是重疊的乘積之和。

從一個左側重疊 $o_{L}$ 到源重疊 $o_{s}$ 的路徑數 $p_{o_{L},o_{s}}$ ，以及
從排水重疊 $o_{d}$ 到右側邊界 $b_{R}$ 的路徑數 $p_{o_{d},o_{R}}$ 。

w(n_{x})=\sum _{o=0}^{|S|^{k-1}-1}p_{o,o_{s}}\cdot p_{o_{d},o}

由於邊界重疊必須區分，因此原像向量是不夠的，路徑數量的資訊包含在原像矩陣中。

D_{L,x-1}(c_{0}c_{1}\dots c_{x-1})\qquad D_{x+1,R}(c_{x+1}c_{x+2}\dots c_{l-1})

計算權重

為了計算所有連線權重，需要從左側邊界到每個單元格的原像計數，以及從右側邊界到每個單元格的原像計數。對於有界格，計數儲存在原像向量中，對於迴圈格，計數儲存在原像矩陣中。

有界格

對於有界格，原像計數儲存為原像向量。左側第一個計數為 $b_{L,0}$ ，右側第一個計數為 $b_{l,R}$ ，它們是邊界向量。

b_{L,0}=b_{L}\qquad b_{l,R}=b_{R}^{T}

左側計數 $b_{L,x}$ 是從左到右計算的，位置 $x$ 的向量是由位置 $x-1$ 的向量計算得來的。右側計數 $b_{x,R}$ 是從右到左計算的，位置 $x$ 的向量是由位置 $x+1$ 的向量計算得來的。

b_{L,x}=D(c_{0}c_{1}\dots c_{x-1})b_{R}^{T}=b_{L,x-1}D(c_{x-1})

b_{x,R}=D(c_{x}c_{x+1}\dots c_{l-1})b_{R}^{T}=D(c_{x})b_{x+1}

所有原像的總數是透過應用兩個邊界計算得出的。

p=b_{L}D(\alpha )b_{R}^{T}=b_{L}b_{0,R}=b_{L,l}b_{R}^{T}

從左到右計數的演算法虛擬碼

b[0] = b_L                     # the left preimage vector b[0] is initialized to the left boundary b_L
for ( x=1; x<=l; x++ )         # run the position index from the left (x=0) to the right (x=l-1)
  b[x] = b[x-1]*D[C[x-1]]      # the new preimage vector is calculated from the old using the
end                            # preimage matrix D[C[x-1]] of the cell value C[x-1] at position x-1

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += b[l][o] * b_R[o]        # the last right preimage vector b[l] and the right boundary vector b_R
end                            #

從右到左計數的演算法虛擬碼

b[l] = b_R                     # the right preimage vector b[l] is initialized to the right boundary b_R
for ( x=l-1; x>=0; x-- )       # run the position index from the right (x=l-1) to the left (x=0)
  b[x] = D[C[x]]*b[x+1]        # the new preimage vector is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += b_L[o] * b[0][o]        # the last left preimage vector b[0] and the left boundary vector b_L
end                            #

示例:

規則 110 中兩個序列的原像圖

迴圈格

對於迴圈格，計數被儲存為原像矩陣，這對於區分連線邊界處每個重疊的計數是必要的。由於格是迴圈的，因此不需要像在有界格中那樣應用邊界向量。

左側計數 $D_{L,x}$ 是從左到右計算的，位置 $x$ 的矩陣是由位置 $x-1$ 的矩陣計算得來的。右側計數 $D_{x,R}$ 是從右到左計算的，位置 $x$ 的矩陣是由位置 $x+1$ 的矩陣計算得來的。

D_{L,x}=D(c_{0}c_{1}\dots c_{x-1})=D_{L,x-1}D(c_{x-1})

D_{x,R}=D(c_{x}c_{x+1}\dots c_{l-1})=D(c_{x})D_{x+1,R}

在每個連線邊界處的 $|S|^{k-1}$ 重疊處，必須分別統計原像的數量 $o_{L}=o_{0}=o_{l}=o_{R}$ 。一個迴圈原像（行）向量 $b_{\circ }(\alpha )$ 是根據原像矩陣 $D(\alpha )$ 的對角元素構建的。

D(\alpha )=D_{0,R}=D_{L,l-1}

b_{\circ }(\alpha )=\left[d_{0,0}(\alpha ),d_{1,1}(\alpha ),\dots ,d_{|S|^{k-1},|S|^{k-1}}(\alpha )\right]

所有原像的總數是迴圈原像向量 $b_{\circ }(\alpha )$ （行）中元素的總和，即與無限制邊界向量 $b_{u}$ （行轉置為列）的標量積。

p=b_{\circ }(\alpha )b_{u}^{T}

從左到右計數的演算法虛擬碼

D[0] = I                       # the left preimage matrix D[0] is initialized to the identity matrix
for ( x=1; x<l; x++ )          # run the position index from the left (x=0) to the right (x=l-1)
  D[x] = b[x-1]*D[C[x]]        # the new preimage matrix is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += D[l-1][o][o]              # the sum of the diagonal elements of the right preimage matrix D(l-1)
  b_0[o] = D[0][o][o]          # the diagonal are copied into the cyclic preimage vector b_0
end                            #

從右到左計數的演算法虛擬碼

D[l] = I                       # the right preimage matrix D[l] is initialized to the identity matrix
for ( x=l-1; x>=0; x-- )       # run the position index from the right (x=l-1) to the left (x=0)
  D[x] = D[C[x]]*b[x+1]        # the new preimage matrix is calculated from the old using the
end                            # preimage matrix D[C[x]] of the cell value C[x] at position x

p = 0                          #
for ( o=0; o<|S|^(k-1); o++ )  # the number of all preimages p is the scalar product of
  p += D[0][o][o]              # the sum of the diagonal elements of the left preimage matrix D(0)
  b_0[o] = D[0][o][o]          # the diagonal are copied into the cyclic preimage vector b_0
end                            #

示例:

規則 110 中兩個序列的原像圖

字串操作

原像網路中的路徑用鄰域和重疊來描述，它們都是細胞序列。由於全域性有效路徑上的鄰域相互重疊，每個細胞可以在 $k$ 個鄰域中找到，也可以在 $k$ 個重疊中找到。

鄰域用原像圖和網路中的連結表示。圍繞細胞 $c_{x}$ 的鄰域 $n_{x}$ 定義為

n_{x}=c_{x-k_{0}}c_{x-k_{0}+1}\dots c_{x}\dots c_{x+k-k_{0}-1}

在原像圖和網路中，重疊用節點表示。包圍單元格 $c_{x}$ 的重疊 $o_{x}$ 定義為：

o_{x}=c_{x+1-k_{0}}c_{x+2-k_{0}}\dots c_{x}\dots c_{x+k-k_{0}-1}

序列可以透過兩種方式表示和操作：

緊湊表示使用代數運算（乘法、除法（無餘數商）和模運算）進行操作
位陣列使用布林邏輯運算（移位、與 OR 融合和與 AND 掩碼）進行操作，每個單元格消耗 $m=top(\log _{2}|S|)$

提取觀察到的單元格

從鄰域提取

代數表示法

c_{x}=n_{x}/|S|^{k-k_{0}-1}\mod |S|

邏輯表示法

c_x = (n_x >> m*(k-k_0-1)) AND (2^m-1)

從重疊提取

代數表示法

c_{x}=o_{x}/|S|^{k-k_{0}}\mod |S|

邏輯表示法

c_x = (o_x >> m*(k-k_0)) AND (2^m-1)

重疊和鄰域之間的轉換

將重疊擴充套件為鄰域

一個鄰域 $n$ （長度 $k$ ）是由一個重疊 $o$ （長度 $k-1$ ）透過在左側或右側新增一個單元格 $c$ 建立的。

字串表示法（單元格字串的連線）

n_{x}=o_{x}c_{x+k-k_{0}-1}

n_{x-1}=c_{x-k_{0}-1}o_{x}

代數表示法

n_{x}=o_{x}\cdot |S|+c_{x+k-k_{0}-1}

n_{x-1}=c_{x-k_{0}-1}\cdot |S|^{k-1}+o_{x}

邏輯表示法

n_x = (o_x << m) OR c

n_x-1 = (c << m(k-1)) OR o_x

將鄰域縮短為重疊

一個重疊 $o$ （長度 $k-1$ ）是由一個鄰域 $n$ （長度 $k$ ）透過在左側或右側刪除一個單元格 $c$ 建立的。

字串表示法

$\alpha \,/\,a$ 表示字串 $\alpha$ 去掉最右側符號 $a$
$b\setminus \beta$ 表示字串 $\beta$ 去掉最左側符號 $b$ )

o_{x}=n_{x}\,/\,c_{x+k-k_{0}-1}\quad \Rightarrow \quad n_{x}=o_{x}c_{x+k-k_{0}-1}

o_{x+1}=c_{x-k_{0}}\setminus n_{x}\quad \Rightarrow \quad n_{x}=c_{x-k_{0}}o_{x+1}

代數表示法

o_{x}=n_{x}/|S|

o_{x+1}=n_{x}mod|S|^{k-1}

邏輯表示法

n_x = o_x >> m

n_x+1 = o_x AND (2^(m*(k-1))-1)

追蹤和回溯演算法

該演算法透過原像圖追蹤路徑。它從最左側未被左側邊界條件遮擋的第一個節點開始。根據位置索引值以及是否存在右側連線，有四種選擇

追蹤第一個未被使用的有效連線到下一個節點，並記錄所選路徑
如果到達的節點在右側邊界，則測試邊界的有效性，並將路徑儲存為原像
如果沒有未被使用的右側連線，則回溯到當前路徑上的前一個節點
當回溯到達左側邊界時，追蹤從下一個有效節點重新開始，直到所有節點都已遍歷。

該演算法可以從右側開始，向左追蹤，獲得相同的原像。方向追蹤的選取方式是為了讓列出的原像按其緊湊表示的升序排序。

形式化演算法描述

該演算法的大部分內容在有界和迴圈格子上是相同的，只有在邊界處有所不同。

主迴圈和左側邊界

主迴圈遍歷可用的追蹤起點。該演算法從左側的第一個重疊開始追蹤 $o=o_{L}=0$ （在有界格子上，被左側邊界遮擋的重疊 $b_{L}$ 會被跳過）。當所有從該重疊開始的追蹤都已遍歷（回溯到達左側邊界 $x=0$ 並且連線索引超過可用連線的數量 $c=|S|$ ）時，追蹤將繼續到下一個有效重疊 $o_{L}=o_{L}+1$ ，直到到達最後一個重疊 $o_{L}=|S|^{k-1}-1$ 。當最後一個重疊的追蹤都已遍歷時，演算法結束。在有界格子上，重疊可能是無限制的，也可能是被邊界向量 $b_{L}$ 遮擋的。在迴圈格子上，所有重疊都被使用。

追蹤

跟蹤會增加當前位置索引 $x=x+1$ 。每次跟蹤步驟都從當前重疊 $o_{x}$ 開始，該重疊位於位置 $x$ ，並跟蹤第一個尚未被跟蹤的連結到排水重疊 $o_{d}$ ，該重疊位於位置索引 $x+1$ 。需要跟蹤 $|S|$ 個連結，如果當前重疊尚未回溯，則跟蹤從連結 $c=0$ 開始，否則回溯提供的連結會被遞增。必須驗證跟蹤步驟的有效性，每個連結都代表一個鄰域 $n=o_{s}c$ ，該鄰域必須指向當前單元格的值 $f(n_{x}^{t-1})=c_{x}^{t}$ 。

如果連結有效，則其索引 $c$ 會被儲存為當前跟蹤路徑上的一個新單元格 $c_{x+k-k_{0}-1}=c$ ，演算法將從排水節點 $o_{d}=c_{x-k_{0}}\setminus o_{x}c_{x+k-k_{0}-1}$ 繼續。
如果連結無效，則跟蹤必須繼續進行下一個連結 $c=c+1$ ，如果沒有剩餘連結 $c=|S|$ ，則演算法將切換到回溯。

回溯

回溯是指在當前路徑上返回，直到找到可用於跟蹤的可用連結。當前沒有進一步路徑的重疊是 $o_{x}$ ，每次回溯步驟都沿著當前路徑上的連結 $n_{x-1}$ 向後移動到位置索引 $x-1$ 處的重疊 $o_{s}$ 。向後的連結 $n_{x-1}=c_{x-k_{0}-1}o_{x}$ 和源重疊 $n_{x-1}=c_{x-k_{0}-1}o_{x}\;/\;c_{x+k-k_{0}-2}$ 是當前路徑上的序列。當回到源單元格時，向前跟蹤的連結從最後一個跟蹤的連結 $c=c_{x+k-k_{0}-2}+1$ 遞增。

右邊界和原像列表

當跟蹤到達右邊界時，列出原像可以開始。

對於迴圈格，當前重疊 $o_{x}$ 與左側的起始重疊 $o_{L}$ 進行比較，如果它們相等，則將長度為 $l$ 的原像 $C^{t-1}=c_{0}c_{1}\dots c_{l-1}$ 新增到原像列表中。
對於有界格，當前重疊 $o_{x}$ 被右邊界向量 $b_{R}$ 掩蓋，如果被接受，則將長度為 $l+k-1$ 的原像 $C^{t-1}=c_{-k_{0}}\dots c_{l+k-k_{0}-1}$ 新增到原像列表中。

對於每個新的原像，原像計數器 $p$ 遞增。

演算法虛擬碼

p=0                               # the preimage counter is initialized to 0
x=0                               # the position index is initialized to 0
c=0                               # the link index is initialized to 0
o_L=0                             # the tracing starts at the first left overlap
while (bounded) then              # if the lattice is bounded
  if ( b[o_L]>0 ) then            # boundary conditions must be checked
    o_L++                         # to ensure the start point is valid
  end_if                          #
end_while                         #
o=o_L                             # the current overlap is initialized

while (o_L<|S|^(k-1)) then        ## main loop ##

if ( c<|S| ) then                 # tracing and right boundary

  if ( x<l ) then                 ## tracing ##
    n=o*|S|+c                     # the neighborhood is created
    if ( f(n)==c_x ) then         # checking it the neighborhood is valid
      o=(o*|S|+c)/|S|^k           # stepping to the new overlap at the right
      C[x+k-k0-1]=c               # storing the link selection cell
      x++                         # incrementing the position index
      c=0                         # at the new overlap start with the first link
    else                          # the selected link is not valid
      c++                         # try the next link
    end_if                        #
  end_if                          #

  else                            ## right and cyclic boundary conditions ##
    if (bounded)                  # for bounded lattices
      if ( b[o]>0 ) then          # check masking of the current overlap with the right boundary vector
        store(C)                  # list the preimage consisting of cells on the current path
      end_if                      #
    end_if                        #
    if (cyclic)                   # for cyclic lattices
      if ( o==o_L ) then          # check if overlaps at the left and right boundary are equal
        store(C)                  # list the preimage consisting of cells on the current path
      end_if                      #
    end_if                        #
    c=|S|                         # to prevent further tracing from the boundary
  end_if                          #
 
else                              # backtracking and left boundary

  if ( x==0 ) then                ## left boundary conditions ##
    o_L++                         # move to the next start point for tracing
    if (bounded) then             # for bounded lattices
      if ( b[o_L]>0 )             # check masking of the left overlap by the left boundary vector
        c=0                       # move to the next start point for tracing
      else                        # else if the current overlap is not valid
        o_L++                     # move to the next start point for tracing
      end_if                      #
    else_if (cyclic) then         # for cyclic lattices
      c=0                         #
    end_if                        #

  else                            ## backtracking ##
    o=(C[x-k0-1]*|S|^(k-1)+o)/|S| # backtracking to the previous overlap
    c=C[x+k-k0-1]                 # restoring the last used link at this overlap
    c++                           # at the backtracked overlap continue with the next link
    x--                           # decrementing the position index
  end_if                          #

end_if

end                               # if all start points are exhausted end the algorithm

演算法複雜度

該演算法可以分為兩個耗時的操作

追蹤和回溯
列出原像

該演算法訪問從起始邊界開始可訪問的所有連結和節點。重疊和鄰域的可訪問性定義為歸納法。

基礎: 起始邊界 $b_{L}$ （這裡指左側）處的重疊 $o$ 可訪問，如果它們是有效的 $b_{L}(o)>0$ 。
歸納: 每個源自可訪問節點的鄰域都是可訪問的。每個指向可訪問且有效鄰域的排放重疊都是可訪問的。

有效的可訪問連結恰好被訪問兩次（第一次在追蹤時，第二次在回溯時），無效連結只被訪問一次（它們的有效性在追蹤時被評估）。追蹤時間的簡單近似值是計算所有可訪問的重疊，必須對邊界處的每個重疊進行計數，因此必須使用原像矩陣進行計數。

任意的重疊 $o_{x}$ 從左側邊界處的有效重疊 $o_{L}$ 可訪問，如果兩者的之間至少有一條有效路徑 $p_{o_{L},o_{x}}>0$ 。位置索引為 $x$ 的重疊的可訪問性可以從原像矩陣 $D_{L,x}$ 中提取，方法是將其元素轉換為布林值或使用布林乘法來計算原像矩陣 $D^{B}$ 。追蹤的演算法複雜度是所有可訪問重疊的總和。

T_{trace}=\sum _{x=0}^{l-1}b_{L}D_{L,x}^{B}b_{u}^{T}

處理時間的上限是觀察到的配置大小 $l$ 的線性函式，但隨著鄰域大小（原像圖大小）的增加而呈指數增長。

T_{trace}=O(l\cdot |S|^{2(k-1)})

列出原像所需的時間 $T_{list}$ 是原像數量 $p$ 的線性函式，其中計算單個原像的時間是配置長度 $l$ 的線性函式。

T_{list}=C_{list}lp=O(lp)\,

演算法的記憶體消耗非常小，只儲存了原像網路中的當前路徑，並在找到有效原像時用於列出。

計數和列出演算法

該演算法包含一個第一階段的反向或計數傳遞，用來計數原像，以及一個第二階段的正向或列出傳遞，用來列出原像。跟蹤和回溯演算法必須追蹤每條連結才能知道它是否會導致有效的原像，而另一方面，計數傳遞會生成關於每個連結是否存在原像以及原像數量的資訊。所有原像都可以在不回溯的情況下列出。

列出傳遞的方向可以反轉，但這裡選擇的方向是為了使列出的原像按照它們的緊湊表示升序排列，計數傳遞則相反。

正式演算法描述

正向（從左到右，生成 $b_{L,x}$ 向量）和反向（從右到左，生成 $b_{x,R}$ 向量）的計數傳遞已經在上面描述，同時計算了原像網路的權重。只需要其中一個傳遞，這裡使用的是反向傳遞。

列出傳遞可以分為初始化和主迴圈中的幾個步驟。

初始化

由於原像的數量 $p$ 已經在計數傳遞中計算出來，因此可以提前為它們分配記憶體。起始重疊陣列 $o_{L}$ 儲存了每個原像（原像網路中的有效路徑）的起始點的值。使用每個起始重疊的原像數量被計算為左側邊界重疊的權重向量。對於有界格，使用左側邊界和從右端到左端的原像計數。

w_{0}(o)=b_{L}(o)b_{0,R}(o)\,

對於迴圈格，使用整個序列的原像矩陣。

w_{0}(o)=D_{0,R}(o,o)\,

起始重疊陣列被複制到當前位置索引 $o_{x}$ 處的重疊陣列中，列出過程可以開始了。

列出

列出從左側邊界 $x=0$ 開始，到右側邊界 $x=l$ 結束。在位置索引的每次遞增中，都會為 $p$ 個原像中的每一個計算一個單元格。

為了簡化演算法，鄰域 $n_{x}$ 中的右側單元格 $x+k-k_{0}-1$ 被儲存。有界格上原像的第一個單元格 $-k_{0}\leq x\leq k-k_{0}-1$ 可以從起始重疊 $o_{0}$ 計算。對於迴圈格，右側的最後一個單元格可以環繞到開頭。

演算法虛擬碼

C = malloc( p * (l+k-1) * |S| )            # reserve memory for the counted amount of preimages
                                           #
i = 0                                      # start with the first preimage
for ( o=0; o<|S|^(k-1); o++ )              # for all overlaps
  for ( j=0; j<b_L[0][o]*b_R[0][o]; i++ )  # for each overlap the number of preimages is calcuated
    o_x[i] = o                             # i-th preimage path begins with overlap o
    i++                                    # to the next preimage
  end_for                                  #
end_for                                    #
if (cyclyc)                                # for bounded lattices there is no need to know the starting points
  o_L = o_R = o_x                          # copy the current array of overlap to the array of starting overlaps
end_if                                     #

for ( x=0; x<l; x++ )                      # run from the left to the right
  i = 0                                    # start with the first preimage
  while ( i< p )                           # check if all preimages have been finished
    for ( c=0; c<|S|; c++)                 # check all links for each source overlap
      o_x[i] = (o_x[i]*|S|+c) / |S|^(k-1)  # calculate the drain overlap
      elseif (bounded)                     # for bounded lattices
        w = b_R[x+1][o_x[i]]               # the count from the drain node to the right end is used
      if (cyclic)                          # for cyclic lattices
        w = D_R[x+1][o_x[i],o_L[i]]        # the count from the drain node to the end node (same as left)
      end_if                               #
      for ( j=0; j<w; j++ )                # use the count
        C[i][x+k-k0-1] = c                 # and write a cell for each of them
        i++                                # increment the preimage counter
      end_for                              #
    end_for                                #
  end_while                                #
end_for                                    # end of algorithm

演算法複雜度

計數的複雜度是配置長度 $l$ 的線性函式。對鄰域大小 $k$ 的依賴關係不是立方的，因為單個單元的前像矩陣中最多有 $k$ 個非零元素。如果格是有界的，計數將儲存為向量，複雜度為線性；對於迴圈格，計數將儲存為向量，複雜度為二次。

T_{count,bounded}=C_{count}lk\,

T_{count,cyclic}=C_{count2}lk^{2}\,

列出的複雜度仍然是配置長度 $l$ 和前像數量的線性函式。

T_{list}=C_{list}l\cdot p

矩陣乘法計數處理前像圖中的所有節點，而先前演算法中的跟蹤和回溯避免了一些節點，從而平均獲得了更低的複雜度。另一方面，該演算法更容易最佳化。

記憶體消耗是另一個缺點，它與計數的時間一樣快地增長。

證明

參考文獻

Andrew Wuensche 和 Mike Lesser，Cellular Automata 的全域性動力學 一維 Cellular Automata 吸引盆域圖集
Wuensche,A.，(1997)，離散網路的吸引盆域，薩塞克斯大學認知科學研究論文 461，D.Phil 論文
Vladimir Batagelj，用於引文網路分析的高效演算法 (2003)
J. C. Seck Tuoh，G. Juárez 和 H. V. McIntosh，計算一維 Cellular Automata 中的祖先，現代物理學國際期刊 C，第 15 卷，第 8 號，第 1151-1169 頁，2004 年 10 月
MathPages
- Cellular Automata
- Cellular Automata 的全域性可逆性
Iztok Jeras，Andrej Dobnikar，計算 Cellular Automata 配置前像的演算法 (PDF)

軟體

DDLab 用於研究 Cellular Automata、隨機布林網路、多值離散動力系統等等的工具；由 Andy Wuensche 提供。
Iztok Jeras，計算 Cellular Automata 配置前像的演算法 TAR.BZ2