元胞自動機/鄰域

一維鄰域

由於在一維中沒有形狀，鄰域的定義通常非常簡單。

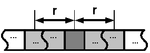徑向鄰域

徑向鄰域

通常一維中的鄰域由其半徑 $r$ 描述，表示從中心細胞向左和向右使用多少個細胞作為鄰域。輸出細胞位於中心。

正式定義

正式來說，徑向鄰域是鄰居的集合

$N=\{-r,-(r-1),\dots ,-1,0,1,\dots ,r-1,r\}$

或者僅僅是鄰域大小 $k=2r+1$，中心為輸出細胞 $k_{0}=r$。

對稱性

• 反射對稱

斯蒂芬·沃爾夫勒姆的記號

在沃爾夫勒姆和其他許多人的著作中，可用的細胞狀態數 $|S|$ 和半徑 $r$ 被組合成一對

$(|S|,r)\,$

另請參閱

• 斯蒂芬·沃爾夫勒姆，元胞自動機的統計力學 (1983)

磚牆鄰域

磚牆鄰域

一個未對齊的鄰域，通常是最小的 $k=2$。輸出細胞位於 $k_{0}=0.5$，位於鄰域的兩個細胞之間。它通常透過交替地將輸出細胞移到 $k_{0}=0$ 和 $k_{0}=1$ 之間來處理。

二維鄰域

馮·諾依曼鄰域

馮·諾依曼鄰域

它是最小的對稱二維對齊鄰域，通常用指南針上的方向描述 $N=\{N,W,C,E,S\}$，有時會省略中心細胞。

正式定義

正式來說，馮·諾依曼鄰域是鄰居的集合

$N=\lbrace \{0,-1\},\{-1,0\},\{0,0\},\{+1,0\},\{0,+1\}\rbrace$

或者矩形鄰域大小的一個子集 $k_{x}=k_{y}=3$，其中輸出單元在中心 $k_{0}x=k_{0}y=1$。

對稱性

• 反射對稱
• 四重旋轉對稱

另請參閱

• [mathworld] - [馮·諾依曼鄰域]

摩爾鄰域

摩爾鄰域

是一個簡單的正方形（通常是 3×3 個單元格），其中輸出單元在中心。通常，鄰域中的單元格由指南針方向描述 $N=\{NW,N,NE,W,C,E,SW,S,SE\}$，有時會省略中心單元格。

正式定義

形式上，摩爾鄰域是鄰居的集合

$N=\lbrace \{-1,-1\},\{0,-1\},\{1,-1\},\{-1,0\},\{0,0\},\{+1,0\},\{-1,+1\},\{0,+1\},\{1,+1\}\rbrace$

或者僅僅是大小為 $k_{x}=k_{y}=3$ 的正方形，其中輸出單元在中心 $k_{0}x=k_{0}y=1$。

對稱性

• 反射對稱
• 四重旋轉對稱

另請參閱

• [mathworld] - [摩爾鄰域]

馬戈盧斯鄰域

可逆的

另請參閱 [1]

未對齊的矩形鄰域

未對齊的矩形鄰域

未對齊的（磚牆）矩形鄰域，通常是最小的 $k_{x}=k_{y}=2$。輸出單元格位於 $k_{0x}=k_{0y}=0.5$ 鄰域的四個單元格之間。它通常透過交替地將輸出單元格移到 $k_{0x}=k_{0y}=0$ 和 $k_{0x}=k_{0y}=1$ 來處理。

六邊形鄰域

六邊形鄰域

六邊形鄰域

對稱性

• 反射對稱
• 六重旋轉對稱

小的未對齊六邊形鄰域

非對齊六邊形鄰域

正式定義

在矩形格子上表示的小（3 單元）非對齊六邊形鄰域正式定義為鄰居集

$N=\lbrace \{0,0\},\{1,0\},\{0,1\}\rbrace$

對稱性

• 反射對稱
• 旋轉對稱性 3 重

參考文獻

• [mathworld] - [Neighborhood]