頂點著色器和可程式設計圖形管道中後續階段最重要的任務之一是將圖元(例如三角形)的頂點從原始座標(例如在 3D 建模工具中指定的座標)變換到螢幕座標。雖然可程式設計頂點著色器允許以多種方式變換頂點,但一些變換通常在頂點著色器之後的固定功能階段執行。因此,在程式設計頂點著色器時,瞭解哪些變換必須在頂點著色器中執行尤為重要。這些變換通常作為統一引數指定,並透過矩陣向量乘法應用於輸入頂點位置(和法線向量)。在具有輸入引數 vertex : POSITION 的頂點著色器中,標準變換可以透過此矩陣向量積計算
mul ( UNITY_MATRIX_MVP , vertex )
Unity 的內建統一引數 UNITY_MATRIX_MVP 將標準頂點變換指定為 4x4 矩陣。(但是,在 Unity 中,建議使用函式 UnityObjectToClipPos(vertex) 執行此變換,該函式也適用於立體投影和投影到 360 影像等。)
雖然這對於點和方向來說很簡單,但正如“應用矩陣變換”一節 中所述,對於法線向量來說就不那麼簡單了。
這裡,我們將首先概述座標系以及它們之間的變換,然後討論各個變換。
相機類比:1. 定位模型,2. 定位相機,3. 調整縮放,4. 裁剪影像 用相機類比來思考變換頂點的整個過程非常有用,如右圖所示。步驟和相應的頂點變換是
定位模型 - 模型變換
定位相機 - 觀察變換
調整縮放 - 投影變換
裁剪影像 - 視口變換 前三個變換在頂點著色器中應用。然後,透視除法(可以認為是投影變換的一部分)在頂點著色器之後的固定功能階段自動應用。視口變換也在此固定功能階段自動應用。雖然固定功能階段中的變換無法修改,但其他變換可以被這裡描述的其他型別的變換所取代。但是,瞭解傳統的變換很有用,因為它們允許充分利用裁剪和對變化變數的透視正確插值。
以下概述顯示了各種座標系之間頂點變換的順序,幷包括表示變換的矩陣
物件/模型座標
具有語義的頂點輸入引數(特別是語義 POSITION)
↓
模型變換 : 模型矩陣 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} unity_ObjectToWorld)
世界座標
↓
觀察變換 : 觀察矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} UNITY_MATRIX_V)
觀察/眼睛座標
↓
投影變換 : 投影矩陣 M projection {\displaystyle \mathrm {M} _{\text{projection}}} UNITY_MATRIX_P)
裁剪座標
具有語義 SV_POSITION 的頂點輸出引數
↓
透視除法 (除以 w 座標)
歸一化裝置座標
↓
視口變換
螢幕/視窗座標
請注意,模型、觀察和投影變換在頂點著色器中應用。透視除法和視口變換在頂點著色器之後的固定功能階段應用。接下來的部分將詳細討論所有這些變換。
模型變換指定從物件座標(也稱為模型座標或區域性座標)到公共世界座標系的變換。物件座標通常特定於每個物件或模型,並且通常在 3D 建模工具中指定。另一方面,世界座標是場景中所有物件的公共座標系,包括光源、3D 音訊源等。由於不同的物件具有不同的物件座標系,因此模型變換也不同;即,必須對每個物件應用不同的模型變換。
模型變換可以用 4×4 矩陣表示,我們將其表示為模型矩陣 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} unity_ObjectToWorld)。它的結構是
M object → world = [ a 1 , 1 a 1 , 2 a 1 , 3 t 1 a 2 , 1 a 2 , 2 a 2 , 3 t 2 a 3 , 1 a 3 , 2 a 3 , 3 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]} with A = [ a 1 , 1 a 1 , 2 a 1 , 3 a 2 , 1 a 2 , 2 a 2 , 3 a 3 , 1 a 3 , 2 a 3 , 3 ] {\displaystyle {\text{ with }}\mathrm {A} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{matrix}}\right]} and t = [ t 1 t 2 t 3 ] {\displaystyle {\text{ and }}\mathbf {t} =\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}
A {\displaystyle \mathrm {A} } t 是一個 3D 向量,表示 3D 空間中的平移(即位移)。 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} A {\displaystyle \mathrm {A} } t 結合在一個方便的 4×4 矩陣中。從數學上來說,模型矩陣表示仿射變換:線性變換加上平移。為了使這種方法起作用,所有三維點都由具有第四座標為 1 的四維向量表示
P = [ p 1 p 2 p 3 1 ] {\displaystyle P=\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}
當我們將矩陣乘以這樣的點 P {\displaystyle P}
M object → world P = [ a 1 , 1 a 1 , 2 a 1 , 3 t 1 a 2 , 1 a 2 , 2 a 2 , 3 t 2 a 3 , 1 a 3 , 2 a 3 , 3 t 3 0 0 0 1 ] [ p 1 p 2 p 3 1 ] {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}\;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]} = [ a 1 , 1 p 1 + a 1 , 2 p 2 + a 1 , 3 p 3 + t 1 a 2 , 1 p 1 + a 2 , 2 p 2 + a 2 , 3 p 3 + t 2 a 3 , 1 p 1 + a 3 , 2 p 2 + a 3 , 3 p 3 + t 3 1 ] {\displaystyle =\left[{\begin{matrix}a_{1,1}p_{1}+a_{1,2}p_{2}+a_{1,3}p_{3}+t_{1}\\a_{2,1}p_{1}+a_{2,2}p_{2}+a_{2,3}p_{3}+t_{2}\\a_{3,1}p_{1}+a_{3,2}p_{2}+a_{3,3}p_{3}+t_{3}\\1\end{matrix}}\right]}
除了第四個座標(它應該是點位的 1),結果等於
A [ p 1 p 2 p 3 ] + [ t 1 t 2 t 3 ] {\displaystyle \mathrm {A} \left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\end{matrix}}\right]+\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}
模型矩陣 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} unity_ObjectToWorld。(另請參見 “應用矩陣變換”部分 。)
嚴格來說,Cg 程式設計師不必擔心模型矩陣的計算,因為它以統一引數的形式提供給頂點著色器。實際上,渲染引擎、場景圖和遊戲引擎通常會提供模型矩陣;因此,頂點著色器的程式設計師不必擔心計算模型矩陣。然而,在某些情況下,在開發圖形應用程式時必須計算模型矩陣。
模型矩陣通常透過組合物件的初等變換的 4×4 矩陣來計算,特別是平移、旋轉和縮放。具體來說,在層次場景圖的情況下,將物件的全部父組(父級、祖父母等)的變換組合起來形成模型矩陣。讓我們看一下最重要的初等變換及其矩陣。
表示向量 t = ( t 1 , t 2 , t 3 ) {\displaystyle =(t_{1},t_{2},t_{3})}
M translation = [ 1 0 0 t 1 0 1 0 t 2 0 0 1 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{translation}}=\left[{\begin{matrix}1&0&0&t_{1}\\0&1&0&t_{2}\\0&0&1&t_{3}\\0&0&0&1\end{matrix}}\right]}
表示沿 x {\displaystyle x} s x {\displaystyle s_{x}} y {\displaystyle y} s y {\displaystyle s_{y}} z {\displaystyle z} s z {\displaystyle s_{z}}
M scaling = [ s x 0 0 0 0 s y 0 0 0 0 s z 0 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{scaling}}=\left[{\begin{matrix}s_{x}&0&0&0\\0&s_{y}&0&0\\0&0&s_{z}&0\\0&0&0&1\end{matrix}}\right]}
表示繞歸一化軸 ( x , y , z ) {\displaystyle (x,y,z)} α {\displaystyle \alpha }
M rotation = [ ( 1 − cos α ) x x + cos α ( 1 − cos α ) x y − z sin α ( 1 − cos α ) z x + y sin α 0 ( 1 − cos α ) x y + z sin α ( 1 − cos α ) y y + cos α ( 1 − cos α ) y z − x sin α 0 ( 1 − cos α ) z x − y sin α ( 1 − cos α ) y z + x sin α ( 1 − cos α ) z z + cos α 0 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{rotation}}=\left[{\begin{matrix}(1-\cos \alpha )x\,x+\cos \alpha &(1-\cos \alpha )x\,y-z\sin \alpha &(1-\cos \alpha )z\,x+y\sin \alpha &0\\(1-\cos \alpha )x\,y+z\sin \alpha &(1-\cos \alpha )y\,y+\cos \alpha &(1-\cos \alpha )y\,z-x\sin \alpha &0\\(1-\cos \alpha )z\,x-y\sin \alpha &(1-\cos \alpha )y\,z+x\sin \alpha &(1-\cos \alpha )z\,z+\cos \alpha &0\\0&0&0&1\end{matrix}}\right]}
繞特定軸的旋轉可以很容易地推匯出特殊情況。例如,這些情況對於實現尤拉角旋轉是必要的。但是,尤拉角有多種約定,這裡不會討論。
一個標準化的四元數 ( x q , y q , z q , w q ) {\displaystyle (x_{q},y_{q},z_{q},w_{q})} 2 arccos ( w q ) {\displaystyle 2\arccos(w_{q})} ( x q , y q , z q ) {\displaystyle (x_{q},y_{q},z_{q})}
還有其他基本的變換,但對模型矩陣的計算而言並不那麼重要。這些或其他變換的 4x4 矩陣透過矩陣乘積進行組合。假設矩陣 M 1 {\displaystyle \mathrm {M} _{1}} M 2 {\displaystyle \mathrm {M} _{2}} M 3 {\displaystyle \mathrm {M} _{3}} M 1 {\displaystyle \mathrm {M} _{1}} M 2 {\displaystyle \mathrm {M} _{2}} M 3 {\displaystyle \mathrm {M} _{3}}
M combined = M 3 M 2 M 1 {\displaystyle \mathrm {M} _{\text{combined}}=\mathrm {M} _{3}\mathrm {M} _{2}\mathrm {M} _{1}\,\!}
請注意,矩陣因子的順序很重要。還要注意,這個矩陣乘積應該從右(向量被乘的地方)讀到左,即 M 1 {\displaystyle \mathrm {M} _{1}} M 3 {\displaystyle \mathrm {M} _{3}}
檢視座標系的示意圖。 觀察變換對應於放置和定向相機(或觀察者的眼睛)。 但是,看待觀察變換的最佳方式是,它將世界座標轉換為位於座標系原點的相機的檢視座標系(也稱為眼睛座標系),(按慣例)指向負 z {\displaystyle z} 正 z {\displaystyle z} x z {\displaystyle xz} y {\displaystyle y}
與模型變換類似,觀察變換由一個4×4矩陣表示,稱為檢視矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} UNITY_MATRIX_V); 但是,它通常與模型矩陣 M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}} M object → view {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{view}}}} UNITY_MATRIX_MV)。 由於模型矩陣先應用,正確的組合是
M object → view = M world → view M object → world {\displaystyle \mathrm {M} _{{\text{object}}\to {\text{view}}}=\mathrm {M} _{{\text{world}}\to {\text{view}}}\mathrm {M} _{{\text{object}}\to {\text{world}}}\,\!}
(另請參見部分“應用矩陣變換” 。)
與模型矩陣類似,Cg 程式設計師不必擔心檢視矩陣的計算,因為它是以統一引數的形式提供給頂點著色器的。 但是,在開發圖形應用程式時,有時有必要計算檢視矩陣。
這裡,我們簡要總結了如何從相機的t 位置、檢視方向d 和世界向上向量k (全部以世界座標表示)計算檢視矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} 負 z {\displaystyle z}
1. 計算(在世界座標中)檢視座標系的 z {\displaystyle z} z ,作為負歸一化的d 向量
z = − d | d | {\displaystyle \mathbf {z} =-{\frac {\mathbf {d} }{|\mathbf {d} |}}}
2. 計算(同樣在世界座標中)檢視座標系的 x {\displaystyle x} x ,透過
x = d × k | d × k | {\displaystyle \mathbf {x} ={\frac {\mathbf {d} \times \mathbf {k} }{|\mathbf {d} \times \mathbf {k} |}}}
3. 在世界座標系中計算檢視座標系 y {\displaystyle y} y
y = z × x {\displaystyle \mathbf {y} =\mathbf {z} \times \mathbf {x} }
使用 x 、y 、z 和 t ,可以輕鬆確定逆檢視矩陣 M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}} t ,並將單位向量 (1,0,0)、(0,1,0) 和 (0,0,1) 對映到 x 、y, 、z 。因此,後面的向量必須位於矩陣 M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}}
M view → world = [ x 1 y 1 z 1 t 1 x 2 y 2 z 2 t 2 x 3 y 3 z 3 t 3 0 0 0 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}x_{1}&y_{1}&z_{1}&t_{1}\\x_{2}&y_{2}&z_{2}&t_{2}\\x_{3}&y_{3}&z_{3}&t_{3}\\0&0&0&1\end{matrix}}\right]}
然而,我們需要矩陣 M world → view {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}} M view → world {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}} M view→world {\displaystyle \mathrm {M} _{\text{view→world}}}
M view → world = [ R t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}\mathrm {R} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}
其中 R {\displaystyle \mathrm {R} } t 是一個 3D 向量。這種矩陣的逆矩陣是
M view → world − 1 = M world → view = [ R − 1 − R − 1 t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}^{-1}=\mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{-1}&-\mathrm {R} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}
在本例中,矩陣 R {\displaystyle \mathrm {R} } R {\displaystyle \mathrm {R} }
M world → view = [ R T − R T t 0 T 1 ] {\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{T}&-\mathrm {R} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]} with R = [ x 1 y 1 z 1 x 2 y 2 z 2 x 3 y 3 z 3 ] {\displaystyle {\text{with }}\mathrm {R} =\left[{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right]}
雖然推匯出這個結果需要一些線性代數知識,但最終的計算只需要基本的向量和矩陣運算,並且可以輕鬆地在任何常見的程式語言中實現。
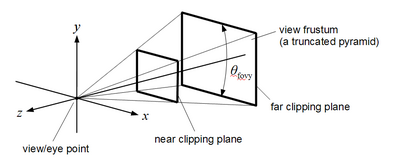
文藝復興時期的透視繪畫:“男人畫魯特琴”由阿爾布雷希特·丟勒創作,1525 年 首先,投影變換決定投影的型別,例如透視或正交。透視投影對應於具有縮短效果的線性透視,而正交投影是不具有縮短效果的正交投影。縮短效果實際上是透過透視除法實現的;但是,控制透視投影的所有引數都在投影變換中設定。
從技術角度來說,投影變換將檢視座標轉換為裁剪座標。(場景可見部分之外的所有圖元部分都在裁剪座標中被裁剪掉。)它應該是頂點著色器中應用於頂點的最後一個變換,在頂點以語義 SV_POSITION 輸出引數返回之前。然後,這些裁剪座標透過 **透視除法** 轉換為歸一化裝置座標,這只是將所有座標除以第四個座標。(歸一化裝置座標之所以被稱為這個名字,是因為它們的值在場景可見部分的所有點的 -1 到 +1 之間。)
與模型變換和檢視變換類似,投影變換也由一個 4×4 矩陣表示,稱為投影矩陣 M projection {\displaystyle \mathrm {M} _{\text{projection}}} UNITY_MATRIX_P)。
與模型檢視矩陣類似,Cg 程式設計師不必擔心投影矩陣的計算。但是,在開發應用程式時,有時需要計算投影矩陣。
這裡,我們展示了三種情況下的投影矩陣(所有情況都是針對 OpenGL 約定,即相機指向檢視座標中的負 z {\displaystyle z}
標準透視投影(對應於 OpenGL 2.x 函式 gluPerspective)
斜透視投影(對應於 OpenGL 2.x 函式 glFrustum)
正交投影(對應於 OpenGL 2.x 函式 glOrtho) 角度 θ fovy {\displaystyle \theta _{\text{fovy}}} 以下是近裁剪平面和遠裁剪平面在 z = − n {\displaystyle z=-n} z = − f {\displaystyle z=-f} 標準透視投影 的特點是
一個角度 θ fovy {\displaystyle \theta _{\text{fovy}}} y {\displaystyle y}
到近裁剪平面的距離 n {\displaystyle n} f {\displaystyle f}
近裁剪平面上中心矩形的寬高比 a {\displaystyle a} 與視點和裁剪平面一起,這個中心矩形定義了視錐體,即對於特定投影變換可見的 3D 空間區域。視錐體外的所有基本圖形和所有基本圖形的部分都被裁剪掉。近裁剪平面和遠裁剪平面是必要的,因為深度值以有限精度儲存;因此,不可能覆蓋無限大的視錐體。
使用引數 θ fovy {\displaystyle \theta _{\text{fovy}}} a {\displaystyle a} n {\displaystyle n} f {\displaystyle f} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ d a 0 0 0 0 d 0 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {d}{a}}&0&0&0\\0&d&0&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]} with d = 1 tan ( θ fovy / 2 ) {\displaystyle {\text{ with }}d={\frac {1}{\tan(\theta _{\text{fovy}}/2)}}}
斜透視投影的引數。 斜透視投影 的特點是
與標準透視投影情況相同,到裁剪平面的距離 n {\displaystyle n} f {\displaystyle f}
座標 r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} a {\displaystyle a} θ fovy {\displaystyle \theta _{\text{fovy}}} 給定引數 n {\displaystyle n} f {\displaystyle f} r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ 2 n r − l 0 r + l r − l 0 0 2 n t − b t + b t − b 0 0 0 n + f n − f 2 n f n − f 0 0 − 1 0 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2n}{r-l}}&0&{\frac {r+l}{r-l}}&0\\0&{\frac {2n}{t-b}}&{\frac {t+b}{t-b}}&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}
正投影的引數。 右圖說明了正投影 ,它沒有透視縮短。引數與斜視投影的情況相同;但是,視錐體(更準確地說,是視體積)現在是一個盒子,而不是一個截斷的金字塔。
使用引數 n {\displaystyle n} f {\displaystyle f} r {\displaystyle r} l {\displaystyle l} t {\displaystyle t} b {\displaystyle b} M projection {\displaystyle \mathrm {M} _{\text{projection}}}
M projection = [ 2 r − l 0 0 − r + l r − l 0 2 t − b 0 − t + b t − b 0 0 − 2 f − n − f + n f − n 0 0 0 1 ] {\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2}{r-l}}&0&0&-{\frac {r+l}{r-l}}\\0&{\frac {2}{t-b}}&0&-{\frac {t+b}{t-b}}\\0&0&{\frac {-2}{f-n}}&-{\frac {f+n}{f-n}}\\0&0&0&1\end{matrix}}\right]}
視口變換的示意圖。 投影變換將檢視座標對映到裁剪座標,然後透過裁剪座標的第四個分量進行透視除法,對映到歸一化裝置座標。在歸一化裝置座標(ndc)中,檢視體積始終是一個以原點為中心的方框,方框內的座標介於 -1 和 +1 之間。然後,該方框透過視口變換對映到螢幕座標(也稱為視窗座標),如相應圖形所示。此對映的引數是視口(螢幕上渲染的矩形)的左下角座標 s x {\displaystyle s_{x}} s y {\displaystyle s_{y}} w s {\displaystyle w_{s}} h s {\displaystyle h_{s}} n s {\displaystyle n_{s}} f s {\displaystyle f_{s}}
glViewport(GLint s x {\displaystyle s_{x}} , GLint s y {\displaystyle s_{y}} , GLsizei w s {\displaystyle w_{s}} , GLsizei h s {\displaystyle h_{s}} );
glDepthRangef(GLclampf n s {\displaystyle n_{s}} , GLclampf f s {\displaystyle f_{s}} );
視口變換矩陣並不重要,因為它在固定功能階段自動應用。但是,為了完整起見,這裡列出它。
[ w s 2 0 0 s x + w s 2 0 h s 2 0 s y + h s 2 0 0 f s − n s 2 n s + f s 2 0 0 0 1 ] {\displaystyle \left[{\begin{matrix}{\frac {w_{s}}{2}}&0&0&s_{x}+{\frac {w_{s}}{2}}\\0&{\frac {h_{s}}{2}}&0&s_{y}+{\frac {h_{s}}{2}}\\0&0&{\frac {f_{s}-n_{s}}{2}}&{\frac {n_{s}+f_{s}}{2}}\\0&0&0&1\end{matrix}}\right]}
傳統的頂點變換在Nvidia 的 Cg 教程第 4 章 中也進行了簡要說明。
傳統的 OpenGL 變換在“OpenGL 4.1 Compatibility Profile Specification”第 2.12 節中進行了詳細描述,該規範可以在Khronos OpenGL 網站 上獲得。Dave Shreiner 編著的“OpenGL Programming Guide”一書的第 3 章(關於檢視)對頂點變換進行了更易懂的描述。該書由 Addison-Wesley 出版。(舊版可在網上 獲得)。
< Cg 程式設計
除非另有說明,本頁上的所有示例原始碼均歸屬公共領域。











![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74f8aaab560e5cb2f74f328599b57b54638f29f6)
![{\displaystyle {\text{ with }}\mathrm {A} =\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}\\a_{2,1}&a_{2,2}&a_{2,3}\\a_{3,1}&a_{3,2}&a_{3,3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dcff6fb39a87563940e5b11f2cd33c100e98d8de)
![{\displaystyle {\text{ and }}\mathbf {t} =\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1762d98b5711974550f359f7b06264db7c931360)

![{\displaystyle P=\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa4c63dd467c6eb272d3b11d2dcb27c641be56bf)

![{\displaystyle \mathrm {M} _{{\text{object}}\to {\text{world}}}\;P=\left[{\begin{matrix}a_{1,1}&a_{1,2}&a_{1,3}&t_{1}\\a_{2,1}&a_{2,2}&a_{2,3}&t_{2}\\a_{3,1}&a_{3,2}&a_{3,3}&t_{3}\\0&0&0&1\end{matrix}}\right]\left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/13d11dfa872a62f11d49f0b7594bea2e57f36ab1)
![{\displaystyle =\left[{\begin{matrix}a_{1,1}p_{1}+a_{1,2}p_{2}+a_{1,3}p_{3}+t_{1}\\a_{2,1}p_{1}+a_{2,2}p_{2}+a_{2,3}p_{3}+t_{2}\\a_{3,1}p_{1}+a_{3,2}p_{2}+a_{3,3}p_{3}+t_{3}\\1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f96ff85224b8f3fb35ccd73c31b54bd69cca25d)
![{\displaystyle \mathrm {A} \left[{\begin{matrix}p_{1}\\p_{2}\\p_{3}\end{matrix}}\right]+\left[{\begin{matrix}t_{1}\\t_{2}\\t_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff6335e75528b3f090325320d6db5f829863e54e)

![{\displaystyle \mathrm {M} _{\text{translation}}=\left[{\begin{matrix}1&0&0&t_{1}\\0&1&0&t_{2}\\0&0&1&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a9ccb86cb24fb7ce0bf772f83efbb7391c312146)






![{\displaystyle \mathrm {M} _{\text{scaling}}=\left[{\begin{matrix}s_{x}&0&0&0\\0&s_{y}&0&0\\0&0&s_{z}&0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b366a6c227cafdd36ec11f98948bc514b42ef014)


![{\displaystyle \mathrm {M} _{\text{rotation}}=\left[{\begin{matrix}(1-\cos \alpha )x\,x+\cos \alpha &(1-\cos \alpha )x\,y-z\sin \alpha &(1-\cos \alpha )z\,x+y\sin \alpha &0\\(1-\cos \alpha )x\,y+z\sin \alpha &(1-\cos \alpha )y\,y+\cos \alpha &(1-\cos \alpha )y\,z-x\sin \alpha &0\\(1-\cos \alpha )z\,x-y\sin \alpha &(1-\cos \alpha )y\,z+x\sin \alpha &(1-\cos \alpha )z\,z+\cos \alpha &0\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68f40eec0dda33d6ffef4c0c25b0586470d62fef)















![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}x_{1}&y_{1}&z_{1}&t_{1}\\x_{2}&y_{2}&z_{2}&t_{2}\\x_{3}&y_{3}&z_{3}&t_{3}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e00ec26b5506a084ce548aef7c370c0097ed34a)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}=\left[{\begin{matrix}\mathrm {R} &\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bcd0a52a1646832fca2af268dd812f7a7cbbc5ca)

![{\displaystyle \mathrm {M} _{{\text{view}}\to {\text{world}}}^{-1}=\mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{-1}&-\mathrm {R} ^{-1}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24280cf60fc5e0c97a0623ca0dea8a080d80b017)
![{\displaystyle \mathrm {M} _{{\text{world}}\to {\text{view}}}=\left[{\begin{matrix}\mathrm {R} ^{T}&-\mathrm {R} ^{T}\mathbf {t} \\\mathbf {0} ^{T}&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c67a2e4ff6d60e39d428d0cac5ab3266f5c1b586)
![{\displaystyle {\text{with }}\mathrm {R} =\left[{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba6f143978631c3e9f3414b755a11e4429c16ee3)






![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {d}{a}}&0&0&0\\0&d&0&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43afae7ea0ce408c5a1a479a265177d988a0fb1c)





![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2n}{r-l}}&0&{\frac {r+l}{r-l}}&0\\0&{\frac {2n}{t-b}}&{\frac {t+b}{t-b}}&0\\0&0&{\frac {n+f}{n-f}}&{\frac {2nf}{n-f}}\\0&0&-1&0\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43a44af0b15159b3378c0d628f98e88f6fa82c86)
![{\displaystyle \mathrm {M} _{\text{projection}}=\left[{\begin{matrix}{\frac {2}{r-l}}&0&0&-{\frac {r+l}{r-l}}\\0&{\frac {2}{t-b}}&0&-{\frac {t+b}{t-b}}\\0&0&{\frac {-2}{f-n}}&-{\frac {f+n}{f-n}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f7345d54b1caa48a201493b48d21f86f2a2321ac)




![{\displaystyle \left[{\begin{matrix}{\frac {w_{s}}{2}}&0&0&s_{x}+{\frac {w_{s}}{2}}\\0&{\frac {h_{s}}{2}}&0&s_{y}+{\frac {h_{s}}{2}}\\0&0&{\frac {f_{s}-n_{s}}{2}}&{\frac {n_{s}+f_{s}}{2}}\\0&0&0&1\end{matrix}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2dccc455d0d455f5128c324abe28d96a952a728d)