電路想法/Deborah Chung 的“表觀負阻”
電路想法:這種排列與負阻現象之間沒有任何聯絡。
1998 年 7 月,Deborah Chung 和 Shoukai Wang 在 布法羅大學 展示了一項實驗的結果,該實驗顯示了裸露的 碳纖維 在壓力作用下表現出表觀絕對負阻。[1]
在實驗中,兩束碳纖維以交叉形狀排列,每束纖維的末端用銅箔和銀漆短路(在影像中的 A、B、C 和 D 處)。電流驅動透過一個分支,電壓測量透過另一個分支。在論文中,電壓除以電流被稱為“表觀電阻”(真正的 電阻 要求電流和電壓在同一位置進行測量。)
論文描述了當纖維被壓縮時,介面表觀接觸電阻如何從正值變為負值。然後,所測量的“負阻”的電流-電壓特性是透過原點的負斜率的直線。表觀負阻也出現在金屬導線(銀包銅)中,但沒有觀察到單根纖維與另一根單根纖維交叉的情況。論文聲稱這種現象很有用,因為同一材料中電子的正向流動和反向流動可以透過外力可重複地控制。
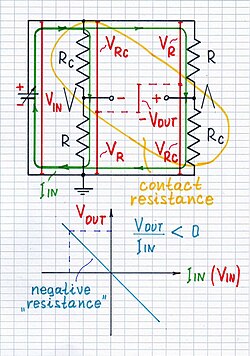
如果我們仔細研究這種奇特的碳纖維排列,我們會意識到它起著某種橋式電路的作用,該電路由兩種電阻組成——穩定的碳纖維電阻 R 和變化的接觸電阻 Rc。以某種方式(目前無法識別),它們被連線到相反的橋臂上。順便說一句,很久以前,我對橋式電路的這個非凡特性印象深刻——反轉輸出電壓。它可以做到這一點,因為輸出電壓是一個差值。它在“飛行”;它是兩個接地電壓之間的差值——VR 和 VRc。根據 R 和 Rc 之間的比例,這個差值可以為零 (R = Rc)、正 (R > Rc) 或負 (R < Rc)。並且,如果我們假設電流 IIN 是輸入量,電壓 VOUT 是輸出量,我們可以將該裝置視為零、正或...“負”跨阻抗轉換器:) 但這不是負阻;它甚至不是阻抗;它是更加抽象的跨阻抗。
 |
 |

|


好吧,讓我們看一下圖 2 並開始思考...... 兩個薄片透過大量接觸電阻 Rc 連線在一起;你可以將中心交叉區域視為一種立方體。電流從正極的頂部薄片流向負極的底部薄片。因此,上面的點 B 是正的,下面的點 D 是負的;輸出電壓 VOUT 具有與圖中所示相同的極性。 “電阻”為正:R = VOUT/IIN > 0。


現在,讓我們看一下圖 3 並繼續一起思考。現在,施加了很大的壓力;因此,兩個薄片透過大量零接觸電阻連線在一起。在這種情況下,中心交叉區域是一個平坦的網格。電流從網格的左側流入,轉向底部,然後從網格的底部流出。在這種情況下,點 D 離輸入電壓源的正極更近,點 B 離負極更近。因此,點 D 比點 D 更正,輸出電壓 VOUT 具有右側圖中所示的負極性。因此,就像 Chung 教授一樣,我們可能會得出錯誤的結論,即“電阻”是“負的”:R = -VOUT/IIN < 0 並開始製造轟動。
最後,我們可以假設在輸出電壓 VOUT 為零的極端限制之間存在一些中等壓力。 “電阻”也為零:R = VOUT/IIN = 0。
那麼,Deborah Chung 教授實際上觀察到了什麼?她做了什麼?讓我們嘗試回答......
很明顯,她製作了一種依賴於施加壓力的奇特橋式電路。實際上,這種碳纖維結構可以充當一個奇特的電壓到電壓轉換器、電流到電壓轉換器,或者充當一個(較差的)壓力到電壓轉換器(壓力感測器)。但在我看來,使用它沒有任何好處;相反,它有許多損失……只要在Google上看看有多少人參與了這個毫無意義的討論,以及浪費了多少精力、時間和金錢……看到人們更多地依賴“信譽”來源而不是他們自己的常識而被誤導,真是令人惋惜!
這個實驗與負阻現象沒有任何聯絡。
這種結構中沒有任何明顯的、絕對的、微分的或動態的電阻;只有普通的、裸露的“19世紀”歐姆電阻。
Chung 的碳纖維網路實際上表現為一個奇特的橋式電路,取決於施加的壓力(就像普通的應變式橋式電路一樣)。
似乎 Chung 的實驗是負阻現象領域的最大誤解。
參考資料
[edit | edit source]- ↑ 碳纖維複合材料中的表觀負電阻 — 王守凱,D.D.L. Chung — 複合材料研究實驗室,紐約州立大學布法羅分校 — 1998 年 4 月 8 日收到;1999 年 3 月 31 日接受
