電路構思/如何產生正弦振盪?
電路構思:將兩個異構能量儲存元件連線在一起,並給其中一個元件充電。

LC 諧振迴路是一個傳奇的電路,在 LC 諧振迴路中產生正弦振盪是一種常見的電氣現象。它在物理、電氣和電子資源中得到了很好的描述(例如,參見網路上關於 LC 諧振迴路的最佳解釋之一[1])。瀏覽這些資源,您可能會了解什麼是 LC 諧振迴路以及它在電氣方面的運作方式。只是,儘管這些資源詳細解釋了 LC 諧振迴路的作用,但它們沒有說明它如何以及為什麼能夠實現這種神奇的效果。
關鍵是 LC 振盪不僅僅是一個特定的電氣現象;它是一個偉大的世界現象。它在“非電氣”世界(力學、氣壓學、液壓學等)中有著許多表現形式。如果您想深入瞭解其本質,您將開始提出許多仍然沒有答案的“哲學”問題。這些問題是什麼?以下列出了一些問題。
為什麼 LC 諧振迴路由兩個“異構”積累元件(電容和電感)組成?為什麼它不由兩個“同構”元件(兩個電容或兩個電感)組成?這些元件在 LC 迴路中的作用是什麼?它們實際上在那裡做什麼?它們是什麼?為什麼 LC 諧振迴路中的能量“永不平靜”?是什麼導致能量在兩個元件之間迴圈(理論上無限迴圈)?是什麼導致積累元件完全放電?為什麼 LC 振盪具有正弦波形?為什麼它不是線性的或其他形狀?為什麼 LC 固有頻率不依賴於“推動”能量的大小?為什麼振盪曲線是對稱的?LC 振盪與其他(RC、弛豫等)振盪有什麼區別?它們之間有什麼相似之處,是什麼?雙元件 LC 諧振迴路與單元件擺之間有什麼聯絡?擺中的“電容”和“電感”是什麼?
在這個故事中,我們將以一種與傳統方式截然不同的方式回答這些問題。在這裡,我們將暫時忘記傳統的“電氣” LC 解釋(例如,“...電感透過電容放電,場崩潰...”);它們並不能幫助我們很好地回答上述問題。因為我們人類不能用具體(電氣)解釋來理解具體(電氣)現象。為了理解具體的電氣概念,我們需要首先揭示具體電氣現象背後的最一般、非電氣概念。
在這個激動人心的故事中,我們,電路構思者和電路哲學家,將嘗試自己找出關於這個偉大世界現象的真相。為此,我們將重新發明並逐步構建著名的 LC 諧振迴路,以便掌握其背後的基本思想。因此,我們將為特定的電氣 LC 現象建立一個通用的、非電氣哲學。
通用源。首先,要在世界上做點什麼,我們需要一個穩定的電源。根據兩種能量 - 動能和勢能,也有兩種電源 - 流狀電源和壓力狀電源(見圖 1a 頂部)。流狀電源保持恆定的流量,而壓力狀電源保持某種物質(空氣、水、油、彈簧張力等)的恆定壓差 - 圖 1b。

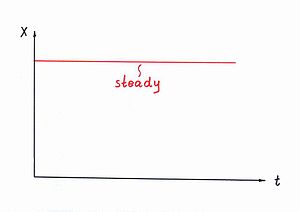
電氣源。類似地,在電氣中,我們也有兩種電源 - 電流源保持恆定電流,而電壓源保持恆定電壓(見圖 1a 底部)。
問題。只是,由於各種原因,我們希望穩定電源的輸出量隨著時間的推移開始週期性變化。當然,我們可以取一個可變電源並開始控制它;但是,我們希望它自發振盪,無需我們的幫助。因此,問題是
首先,我們必須使穩定量依賴於(隨著)時間而變化。此時,它如何隨時間變化並不重要;重要的是它隨時間變化。因此,主要問題是:我們如何產生隨時間變化的數量?
哲學。顯然,我們必須在時間內開始某個過程(但時間是什麼?:)為了使某物發生變化,我們必須從它那裡獲取或賦予它;這意味著要將某物從一個地方移動到另一個地方...一個電源不足以實現此目的,因為它保持其輸出量的穩定性;我們需要兩個元件 - 源和負載相互連線,以開始將能量從源傳輸到負載(以及可能相反)。我們已經有一個電源;剩下的就是選擇負載型別。
積累的需求。電阻在這種情況下是無用的,因為它可以瞬時改變電流(當電壓瞬時改變時)。電阻不能儲存能量,它不能“記憶”。很明顯,我們必須開始將一些量傳輸並存儲在一個積累元件(一個積分器)中。積分器可以積累能量、物質或資訊;它們主要儲存能量。因此,我們可以透過持續向積累器新增能量來使其輸出量增加,並透過持續從積累器中減去能量來使其輸出量減少。根據兩種能量 - 動能和勢能,我們可以構建兩種型別的積分器 - 流到壓力和壓力到流積分器。
流壓積分器。 在這種情況下,我們開始將一個類流量(攜帶動能)轉換為一個類壓力(攜帶勢能),並將其儲存到一個具有包含屬性的累積元件中(參見圖 2a 的頂部)。能量從流動轉移到壓力累積器,類壓力量隨著時間的推移線性變化(圖 2b)。
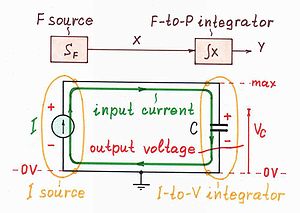

示例: 移動的質量推一個彈簧,一個加速的擺錘升起,一個孩子上緊發條電機,一個弓箭手拉弓,一個飛輪使玩具汽車運動,一個電機舉起一個質量,一個氣泵充氣輪胎,一個水泵填充水庫等等。我們甚至可以為了感受這個過程,想象我們自己在移動(在聯想思維中,這種創造性思維技巧被稱為“移情”)。
請注意,流壓積分器由兩個相互連線的異質元件組成 - 動能源和勢能累積器。如果我們將兩個同質元件相互連線(一個動能源和一個動能累積器),就會出現一個很大的壓力,並且過程會暫時停止;這種安排將進行微分而不是積分。一個機械示例:想象一下,如果一輛移動的汽車撞上一輛靜止的汽車會發生什麼。
電流-電壓積分器。 在電學中,我們有兩種可以累積能量的元件 - 電容器儲存勢能,電感器儲存動能。因此,我們可以構建兩種型別的電積分器 - 電流-電壓積分器和電壓-電流積分器。讓我們從第一個也是最流行的開始。
根據一般流壓佈置,在電流-電壓積分器中,我們開始將電流(攜帶動能)轉換為電壓(攜帶勢能),並將其儲存到電容器中。因此,該電路包括一個為電容器充電的電流源(參見圖 2a 的底部)。結果,電容器兩端的電壓隨時間線性變化(圖 2b)。請注意,電流進入電容器的正極板;因此,電容器在這裡充當負載。
該電路由兩個相互連線的異質電元件組成 - 電流源和電容器。如果我們將兩個同質元件相互連線(一個電流源和一個電感器),它們之間會出現高電壓,並且過程會暫時停止;該電路將進行微分而不是積分。
圓弧...
[edit | edit source]到目前為止,我們已經使穩定量隨時間線性變化。因此,我們獲得了隨時間不斷增加的量。在許多情況下(例如,在斜坡發生器中),這是一個理想的特性;但在這裡,我們需要正弦形狀,而不是線性形狀。所以,新的問題是,“我們如何將線性曲線圓化?”
然後,讓我們仔細檢查當前的線性曲線,試圖找到將其轉換為正弦形狀的補救措施。這意味著什麼?這意味著在量線性變化一段時間後,此時它已經開始改變(減小)其斜率,彎曲,"失去勇氣"(圖 3b)。我們如何實現這樣的效果?
總體思路。 到目前為止,我們已經透過一個對恆定量進行積分的積分器獲得了線性變化。現在,我們問自己,“我們如何使積分器減緩其輸出量的變化?”答案是:“透過減小輸入量。” 這是所需的基本思想 - 減小輸入量。
...透過降低有效電壓...
[edit | edit source]記住不完美的 RC 積分器,其線性曲線自然圓化(呈指數形狀)。


這個積分電路(圖 3a)的“問題”(在這裡,這是一個優點)是電容器正在被一個不完美的“自制”電流源(由電壓源 V 和電阻 R 組成)充電。結果,負載(電容器)上的電壓降 VC 使激勵電壓 V 虛弱;透過這種方式,它會干擾不完美的電流源。在這種情況下,電壓差 VR = V - VC 決定電流 I 而不是激勵電壓 V。隨著建立電流的電壓 VR 隨時間減小,電流也減小。由於這種隨時間減小的電流源,VC 的曲線也開始減小其斜率;這就是我們在這裡想要的。
...透過減小輸入電流...
[edit | edit source]但這裡我們有一個完美的電流源,其電流不依賴於負載(電容器)上的電壓。這意味著,如果負載電壓升高,我們的電流源也會增加其內部激勵電壓,從而消除電壓干擾。[2] 這看起來很奇怪,但這裡的問題恰恰是完美的電流源:) 那麼我們該怎麼辦?我們如何使其表現得不完美?
看著圖 3,我們腦海中可能會開始形成一些新想法的萌芽... 事實證明,我們可以透過某種方式使完美的電流源開始自動減小負載電壓升高時產生的電流,從而設法圓化、改變並最終減小曲線的斜率... 我們可以概括這個斷言
而在不完美的 RC 積分器中,圓化是降低有效建立電流的電壓 VR 的結果,而在這裡,圓化將是降低整個輸入電壓 V 的結果。好吧,這很棒,但我們如何實現這種魔法?
當然,我們可以調節輸入電壓,但這將需要一些電子電路。請不要忘記,在這裡我們“發明”了可以振盪的最簡單的“東西”;因此,我們需要最簡單的“技巧”!是什麼?
...透過耗盡輸入電流源
[edit | edit source]看起來另一個新的想法開始形成... 我們想減少一個量... 它是由電源產生的... 它有一個有限的能量儲備... 哈哈!如果我們開始從電源中取走能量,它的輸出量就會開始減小!這裡有一些例子:推彈簧,移動的質量開始減速;撞到彈性障礙物,我們會減慢你的跑步速度;上升,擺錘開始減速,等等。


正確的想法。 如果以某種方式,輸入電流源開始減弱、消耗、耗盡其能量儲備,電流源的電流也會開始減小(圖 4a)。結果,電容器兩端的電壓將開始緩慢變化,並且其曲線將開始“失去勇氣”(圖 4b)。這個源是不是像上面那樣一個不完美的電流源?不,它不是;它是一個正在耗盡但仍然是完美的恆定電流源,它逐漸降低其輸出量。在這裡,電流的減小不是因為負載電壓(就像不完美的 RC 積分器那樣),而是因為負載消耗!
什麼電氣元件可以充當這樣的耗盡的完美電流源?當然,一個充滿動能的電感器!這看起來很奇怪,但它會產生一個“恆定”的電流(對於快速負載變化),並且該電流會逐漸減小
哈哈!我們已經獲得了所需的佈置(圖 4a);我們幾乎“發明”了 LC 振盪電路
請注意,電流離開電感器的正極引線;因此,電感器在這裡充當源。
停止“運動”
[edit | edit source]我們已經到達了曲線的頂端,現在是時候在這裡停下來了。但是我們如何使積分器的輸出量停止?如果我們停止輸入量,它會停止嗎?不會。即使我們將輸入量顯著降低,積分器也不會停止改變其輸出量。停止積分器輸出量的唯一方法是將輸入量歸零。為了說服你自己相信這種現象,想象你用一個容器裝滿了水:即使你將流量降低到一個微不足道的量,水位仍然會繼續上升。更多例子:如果你用零錢逐漸補足一個存款,那麼金額會隨著時間的推移而緩慢增加(但仍然增加);推彈簧,移動的質量最終會停止;移動的擺錘在頂部停止。


上面提到的“耗盡”流源 above,它產生逐漸減小的流量,已經幫助我們改變了曲線的斜率並使其變得圓滑。現在,在曲線的頂端,它可以幫助我們停止“運動”。實際上,在數量達到最大值時,該源已完全耗盡其動能儲備。實際上,在這個時刻,它不僅僅是一個源;它是一個空源。因此,流量變為零(圖 5a),積分器停止改變其輸出量(圖 5b)。然後,讓我們得出另一個結論
在電氣實現(LC 諧振迴路)中,電感器充當耗盡電流源(圖 5a)。在曲線的頂端,它已完全放電,不再產生電流。因此,電容器兩端的電壓停止變化。
為什麼電感器完全放電?我們已經 said 電感器是一個耗盡的,但仍然是完美的恆流源。此外,電感器是一個自然的、純淨的、整體的電流源;它不是一個人工的電流源,它不像 imperfect RC integrator 中那樣由內部電壓源和電阻組成。這意味著它可以在負載上產生足夠高的電壓來產生所需的電流。換句話說,電感器產生的電流不依賴於電容器兩端的電壓;該電壓不是電流的“阻力”。由於沒有任何東西阻礙電感器產生的電流,無論電感器中剩餘多少能量,電流都會持續流動,直到電感器完全放電。
相反的安排。為了感受這種差異,將這種“放電電感器 -> 充電電容器”的安排與 下面 提到的“放電電容器 -> 充電電感器”的安排進行比較。在後一種情況下,帶電的電容器正在放電,空的電感器正在充電。這樣,這兩個元件最終都帶有一些能量。它們兩端的電壓具有某個中間值 - 系統平衡點。
到目前為止,我們一直在一個方向上“移動”(最初快,然後慢),最後我們在曲線的頂端停了下來。由於我們一直在不斷地將能量“推入”累加器(積分器),因此其輸出量一直在不斷地增加。因此,我們得到一個單調且相當無趣的訊號:) 然而,我們希望得到一個週期性的量;所以,我們在這裡,在曲線的頂端,以某種方式改變“運動”的方向。在這點上必須發生某些事情才能使積分器的輸出量開始減少... 什麼會導致這種情況發生?
檢視許多積分的類比,我們可以得出結論,改變積分器(這裡是一個類似壓力的)輸出量方向的唯一方法是改變其輸入(這裡是一個類似流動的)量的方向,而不是其大小。再次想象水流的類比:當我們給容器注水時,水位會上升;為了讓它下降,我們必須開始清空容器。或者想象一下金錢的類比:當你逐漸增加存款時,隨著時間的推移,金額會增加;為了讓它減少,你開始“清空”存款。當然,我們應該再次提到著名的機械類比:移動的質量停止後,彈簧開始將它擊回;在我們撞擊彈性屏障後,它會反彈我們,它就像一種“反轉器”,改變了我們的運動方向。我們已經準備好得出兩個結論
但是這個積分器不僅僅是一個簡單的累加器... Remember 到目前為止,一個類似流動的源一直在緩慢地耗盡併為這個壓力累加器(一個流到壓力的積分器)充電。因此,在這個過程結束時,積分器已經轉變為相反的壓力源。現在,它是一個充滿能量的累加器;它已經成為一個電源!因此,它可以自行透過負載傳遞電流來改變其輸出量。但這裡的負載是什麼?另一個元件(前源)現在充當負載。它是什麼型別的負載? Remember 它是一個儲存動能的累加元件。
壓到流的積分器。因此,我們現在開始將一個類似壓力的量(攜帶勢能)轉換為一個類似流動的量(攜帶動能),並將其儲存在一個具有慣性特性的累加元件中(見圖 6a 的頂部)。現在,能量以相反的方向移動 - 從壓力累加器到流量累加器,並且類似流動的量應該隨著時間的推移線性變化(圖 6b)。


示例:彈簧(或重力)使質量運動,彈簧馬達驅動玩具,孩子加速飛輪汽車,儲存在儲氣罐中的壓縮空氣旋轉空氣渦輪機,儲存在湖泊中的水旋轉水輪機,巨石從山上滾下來,速度越來越快,“踩油門”使恆功率發動機推動汽車加速,從氣球火箭中逸出的加壓空氣使其加速飛行,水火箭,“用腳推”使腳踏車開始運動,等等。
請注意,這種安排再次包括兩個連線在一起的異類元件 - 一個勢能源和一個動能累加器。如果我們將兩個同類元件連線在一起(現在,一個勢能源和一個勢能累加器),就會產生一個大電流,並且該過程會立即停止。正如 above,這種安排將進行微分而不是積分。
電壓到電流的積分器。根據一般的壓到流安排,在電壓到電流的積分器中,我們開始將電壓(攜帶勢能)轉換為電流(攜帶動能),並將其儲存在電感器中。因此,該電路包括一個為電感器充電的電壓源(見圖 6a 的底部)。因此,電感器中的電流應該隨時間線性變化(圖 6b)。請注意,電流離開電容器的正極板(因此,它在這裡充當源),電流進入電感器的正極板(因此,它在這裡充當負載)。
該電路由兩個連線在一起的異類元件組成 - 電壓源和電感器。如果我們將兩個同類元件連線在一起(一個電壓源和一個電容器),就會有一個大電流流過它們,並且該過程會立即停止;該電路將進行微分而不是積分。
耗盡的電壓源 如 above,為了使曲線變圓滑,我們的源必須具有有限的能量儲備;它必須逐漸耗盡,逐漸減少。電容器恰好充當這種耗盡的電壓源。只是,我們 before 希望在最後部分使曲線變圓滑,而這裡我們希望在初始部分使曲線變圓滑。讓我們看看情況如何。在開始時,電流很小,電感器消耗的能量很少。後來,流經電感器的電流增加,它開始從電壓“源”中消耗越來越多的能量。太棒了!曲線在其初始部分變圓滑,正如我們所期望的那樣!
在這個階段結束時,該源已完全耗盡其勢能儲備。如上所述,在這個時刻,它不是一個源;它只是一個空的源。因此,壓力變為零(見圖 7a 的頂部),壓到流的積分器停止增加其輸出量(圖 7b)。它在這個時候積累了最大的動能。
如果你再次檢視我們最喜歡的類比,你會發現上面所有機械示例中的移動質量都被最大限度地加速(例如,想象一下我們在這個時候跑得有多快:) 這裡,我們必須記住,這些物體有一個有趣的特性 - 慣性。如果它們沒有慣性,它們就會在這個時候停止,並且系統將處於平衡狀態。但它們有慣性;這就是為什麼,它們會越過這個零點(中性位置)並繼續運動... 就好像有一些惡魔般的力:) 使它們繼續越過這個點(記住牛頓運動定律)。


我們已經可以比較兩種不同累加元件的行為。我們 already 已經看到了勢能累加器(電容器)如何充當一種彈性屏障,它會反彈移動的“質量”,從而反轉運動的方向。現在,我們可以看到動能累加器(電感器)由於其固有的慣性,“越過”平衡點(零電平)並繼續“移動”。
不久前,電容器充當著耗盡的電壓源。此時,它已經完全放電,並且在其兩端沒有電壓。電感器中的電流達到最大速率,但它已經停止變化。因此,在這個階段結束時,電流和能量消耗都增加到最大值。
相反的安排。我們已經成功地回答了為什麼 電感器 會透過電容器完全放電 - 因為它是一個自然的真正電流源。現在情況更加有趣。為了回答為什麼電容器會完全放電,讓我們再次考慮 相反的安排 - 一個帶電的電容器連線到一個空的電容器。如果你喜歡類比,想象一下兩個連通的容器,其中一個容器是滿的,另一個是空的。我們知道結果:一開始會有很大的電流;最初空電容器兩端的“相反”電壓(最初空容器的水位)開始迅速上升;結果,它下降並最終停止電流。此時,能量分佈在兩個電容器之間,系統處於靜態平衡(記住牛頓第三定律)。最初帶電的電容器並沒有完全放電。
為什麼電容器會完全放電?相反,如果我們將帶電的電容器連線到一個最初空的電感器(本例中的情況),電流在一開始是微不足道的,電容器開始緩慢地透過電感器放電。隨著時間的推移,電感器允許電流逐漸增加。增加的電流越來越多地放電電容器,從而加快其放電速度;最後,電容器完全放電。形象地說,電感器具有時間相關的行為:在一開始,它消耗的電流很少,但最終它會吞噬大量的電流(電容器具有相反的時間相關的行為 - 一開始,它會吞噬最大的電流,但最終它消耗的電流很少)。
乍一看,似乎系統正在向平衡狀態移動;我們可能會假設它已經成功地到達了這一點,並且居住在 LC 振盪迴路中的能量“已經找到了安寧”...
建立正弦曲線的後半部分
[edit | edit source]到目前為止,我們一直在詳細地考慮如何建立正弦曲線的前半部分(第一和第二象限)。常識表明,我們可以用相同的方式建立後半部分。那麼,讓我們試一試。
第三象限
[edit | edit source]

在第二象限結束和第三象限開始時,情況與第一象限相同。一方面,電感器充滿動能,並且再次從積分器轉變為電流源(圖 8a)。另一方面,空電容器連線到此“電流源”。那麼電感器會開始做什麼呢?當然,它將開始給電容器充電並開始逐漸放電。唯一的區別是電流的方向,它在電容器兩端產生負電壓。結果,曲線開始下降(一開始是迅速下降,然後是緩慢下降)並最終在底部停止。正如我們所期望的,它在最後的部分是圓形的。
第四象限
[edit | edit source]

類似地,在最後第四象限的開始,情況與第二象限相同。一方面,電容器充滿勢能,並且再次從積分器轉變為電壓源(圖 9a)。另一方面,空電感器連線到此“電壓源”。那麼電容器會開始做什麼呢?當然,它將開始給電感器充電並開始逐漸放電。唯一的區別是電容器兩端的負電壓,它會產生具有相反方向的電流。結果,曲線保持在零點以下,但開始上升(一開始是緩慢上升,然後是迅速上升)並最終穿過零點(圖 9b)。正如我們所期望的,它在最初的部分是圓形的。
概括
[edit | edit source]在這個不可思議的故事的結尾,讓我們概括一下我們所做的事情。
基本結構
[edit | edit source]
在一開始,我們組裝了一個系統,該系統由兩個相互連線的異質元素組成,這些元素可以處理兩種不同的能量:它們可以轉換能量(充當真正的能量轉換器)、儲存能量(充當累加器)和供應負載能量(充當源)。其中一個可以將勢能轉換為動能、儲存動能並將此動能逐漸轉移到負載,從而保持逐漸減小的流動量;另一個元素可以將動能轉換為勢能、儲存此勢能並將此勢能逐漸轉移到負載,從而保持逐漸減小的壓力量。第一個元素具有慣性的屬性,而第二個元素具有應變的屬性;因此,第一個元素可以“越過”平衡點並繼續運動,而第二個元素可以反轉“運動”的方向。這些可逆元素中的每一個都可以充當負載,也可以充當逐漸耗盡的源。這些型別的可充電源彼此完美地匹配 - 當一個元素充當流量輸出源時,另一個元素充當流量輸入負載,反之亦然 - 當另一個元素充當壓力輸出源時,第一個元素充當壓力輸入負載。結果,它們可以隨著時間的推移逐漸地彼此交換能量。
電路
[edit | edit source]在電氣中,我們透過將電感器和電容器連線在一起實現了這種安排;因此,我們獲得了著名的LC 振盪迴路。電感器可以將電壓轉換為電流,將移動電子在磁場中的動能儲存起來,並將此動能逐漸轉移到負載,從而保持逐漸減小的電流;電容器可以將電流轉換為電壓,將此勢能儲存到靜電場中,並將此勢能逐漸轉移到負載,從而保持逐漸減小的電壓。簡單地說,電感器充當可充電電流源,而電容器充當可充電電壓源。
操作
[edit | edit source]在一開始(參見圖 11 中的點a),LC 振盪迴路中沒有能量;它處於靜止狀態。然後,我們透過短暫地連線一個電流源來給電感器充電(我們也可以透過短暫地連線一個電壓源來給電容器充電,而這在電子振盪器中是更常見的情況)。在我們斷開電源後,奇蹟開始了...

階段 1。電感器(充當正電流源)透過電容器(充當累加負載)逐漸放電。能量從左向右移動;電壓上升到零點以上。在頂部(點b),電容器成為一個正電壓源。
階段 2。電容器(充當正電壓源)透過電感器(充當累加負載)逐漸放電。能量從右向左移動;電壓下降到零點以下。最後(點c),電感器成為一個負電流源。
階段 3。電感器(充當負電流源)透過電容器(充當累加負載)逐漸放電。能量從左向右移動;電壓下降到零點以下。在底部(點d),電容器成為一個負電壓源。
階段 4。電容器(充當負電壓源)透過電感器(充當累加負載)逐漸放電。能量從右向左移動;電壓上升到零點以上。最後(點e),電感器成為一個正電流源。
組裝。如果電路中沒有損耗,四個階段將連續地一個接一個地重複(1 - 2 - 3 - 4 - 1 - 等),從而形成完整的 LC 正弦振盪(圖 11)。LC 振盪迴路保持最初注入的能量完整,但這種能量並不處於靜止狀態,它“沒有安寧”。居住在 LC 振盪迴路中的能量在兩個元件之間連續地來回移動,並交替地從一種形式變為另一種形式。因此,代表相應能量型別(動能和勢能)的電量(電流和電壓)以正弦方式變化;因此,我們可以將它們用作輸出。
能量獨立性。正如我們所見,在我們將能量注入 LC 諧振電路後,它就開始產生一個具有自然週期的正弦振盪。如果我們注入更多的能量,電壓和電流的振幅會增加,但它們的變化也會更快,反之亦然;因此,自然週期保持不變。這種“能量無關的時間行為”的原因是可變消耗:當我們增加最初注入的能量時,消耗也會增加,反之亦然。在用更多能量為電感器充電的情況下,透過電感器的電流將達到更大的幅度,然後,當我們斷開“推動”電流源時,這個更大的電流將決定更大的消耗;因此,時間保持不變。在另一種情況下,當我們用更多能量為電容器充電,然後斷開“推動”電壓源時,電感器將開始逐漸消耗更大的電流;因此,時間再次保持不變(我們可以在RC 電路中觀察到類似的“時間常數”效應)。因此,我們可以得出結論:LC 振盪的自然頻率不依賴於“推動”能量的多少(電壓和電流的幅度)。
LC 依賴性。相反,如果我們改變蓄能元件(電感器和電容器)的“儲存屬性”(電感 L 和電容 C)的值,自然頻率也會改變。我們可以很容易地從直覺上認識到,儲存屬性的值越大,相應四分之一週期的持續時間就越長(例如,如果電容器“更大”,電感器需要更多時間來為其充電)。
對稱性。但是為什麼振盪仍然是對稱的(TPhase1 = TPhase2 = TPhase3 = TPhase4),即使我們只改變一個儲存屬性(電感 L 或電容 C)的值?答案很簡單。在每個半週期內,兩個元件中的每一個都會兩次改變其“角色”:在第一個四分之一週期內它充當負載,在第二個四分之一週期內它充當電源。這樣,它的儲存屬性決定了相鄰兩個四分之一週期的持續時間;改變該屬性,我們同時改變兩個四分之一週期的持續時間。因此,當我們改變電感 L 或電容 C 或兩者時,曲線保持對稱。
LC 諧振電路是最簡單的可以產生具有完美正弦形狀振盪的電路。這種獨特的電路僅由兩個元件組成,但它可以自行完成產生正弦振盪所需的一切。它是一個幾乎理想的電路,類似於永動機:) - 我們只需要注入初始能量,然後它就可以自行持續執行。
振盪 是維基百科關於自然界振盪的一篇通用文章。
- ↑ 一個電擺 by Tony Kuphaldt 是一個經典但可能是關於 LC 諧振電路操作的最好書面故事,儘管它似乎暗示擺表現出簡諧運動(它們不是,完全)。
- ↑ 透過跟隨激勵電壓保持恆定電流揭示了恆定電流源的原理。
- 振盪器簡介 和
- LC 振盪器 很好地展示了 LC 諧振電路操作的經典“電氣”觀點。
- 並聯 LC 電路如何儲存能量 是另一個優秀的 LC 資源。
- 關於 LC 電路的講座 是一系列包含有用公式的幻燈片。
- LC 諧振電路 是一個關於 LC 諧振電路的有趣且圖文並茂的故事。
- 共振的物理學 是一個經典但寫得很好的關於 LC 諧振電路操作的故事。
- 特斯拉線圈的工作原理 對 LC 諧振電路有一個簡明但資訊豐富的介紹。
- LC 電路 對電氣和機械實現進行了比較。
- 電感器 - 關於電感器行為的優秀材料。
