電路創意/在電阻薄膜上行走

<<< 目錄 - 頁面階段 >>>

透過電壓圖"發明"各種電阻電路 （現在重現著名的歐姆實驗）

電路創意：窺視一個電壓供電的線性電阻器，顯示電阻薄膜上的電壓分佈。

“發明”的器件：運動到電壓轉換器，分壓器，電阻疊加器和減法器，反相放大器.

開始：歐姆實驗

歷史。 幾乎三個世紀前，歐姆進行了他的著名實驗。在那個黑暗時代，物理學家試圖解釋為什麼不同導線之間存在明顯的差異，什麼是電流，以及它與靜電之間的關係；對他們來說，電流和電壓的概念是抽象的，幾乎是上帝自己揭示的。正如他們所說，他拉伸了一段長度為 L、電阻為 R 的銅線；然後，他在導線上施加了電壓差。由於歐姆在 19 世紀初進行了他的實驗，他唯一能用作電源的只有由亞歷山德羅·伏特發明的電池的前身。不幸的是，這個實驗失敗了，因為歐姆使用了一根電阻非常低的導線，因此電源負載過重，普通的伏特電池無法正常工作。因此，歐姆決定利用塞貝克剛剛發明的熱電效應制造一個良好的電壓源。因此，電壓差的來源是一個熱電偶；1820 年代可用的其他電源太不可靠了。歐姆將熱電偶的一端浸入沸水中，另一端浸入放在三腳架上的小容器中的融化的冰中。然後，使用驗電器（請記住，在那個時代他們沒有 3 美元的萬用表：），一塊磁化針，也許還有大量的想象力，歐姆開始研究“電阻器”上的電壓分佈。

重現歐姆定律。 在實驗室中重現歐姆實驗非常有趣、激動人心和重要，因為歐姆定律是電子電路的基礎，電氣工程專業的學生都在學習。這是一個好主意，如果在電子課程的實踐練習和理論課上，學生和老師一起重新發明一切，每一個單一元件（甚至是電阻器）。所以我們開始想象歐姆是如何做他的著名實驗，並找到了電流、電壓和電阻之間的基本關係。這樣，現在使用現代測量儀器和毫不遜色的想象力來重現著名的歐姆實驗，我們可以“發明”各種有價值的無源電阻電路。

搭建實驗室裝置。 為了進行歐姆的真實實驗，我們需要一根電阻絲、導線、一個電源、一個電壓表和一個電流表。一條總電阻為 10 Ω 的加熱器上的 50 釐米長的導線充當電阻絲。絕緣銅線充當導線。一個可變電源可以產生高達 40 V/2.5 A 的電壓。我們將使用兩種電壓表和電流表 - 老式指標式和 VOM 數字式。

水力類比：壓力圖

一個有分支的管道（沒有流動）

讓我們從考慮一個眾所周知的水力類比（管道）開始 - 我們可以在周圍看到它。例如，想象一個裝滿水的巨大容器，它供應一根細長的管道；讓我們先將管道分支（圖 1）。問題是：“管道內的壓力是多少？”更準確地說，“沿管道的區域性壓力是多少？” 不會有太多人能正確地回答這些簡單的問題。

我們可以瞭解，如果我們沿著管道等間隔鑽一些小孔（如果我們想更精確，我們可以垂直地插入一些充當區域性壓力錶的細玻璃管）。結果是我們意料之中的：所有水位（因此，沿管道的所有區域性壓力）都相等。這張圖顯示了沿管道的壓力分佈；我們可以將其稱為“壓力圖”。

一個開啟的管道（有流動）

現在開啟管道（圖 2）；水將開始流動。這是我們日常生活中眾所周知的現象，有人在管道末端開啟水龍頭。在左側，水壓最大；在右側，水壓最小。但是現在沿管道的區域性壓力是多少？我們的直覺告訴我們，區域性壓力將從左到右逐漸減小。

實際上，水柱的高度（因此，沿管道的區域性壓力）從左到右逐漸減小。壓力圖的包絡線是一個三角形。

電氣領域：電壓圖

一個開路的電路（沒有電流）

現在讓我們將這些概念轉移到我們的電氣領域，看看沿電阻絲的電壓是否以相同的方式分佈。這意味著在今天的條件下重現歐姆的真實實驗。

現在，將導線的兩端固定在瓷絕緣端子（支架）上，先對導線的左側施加電壓（例如，10 V）（圖 3）。在這種情況下，我們可以研究什麼？我們用電壓表測量什麼？通常的觀點是將電阻器視為一個點，一個沒有尺寸的東西，一個只有電阻屬性的兩端元件。但在這裡，我們有獨特的機會窺視“電阻器”內部！當你沿著導線“看”時會“看到”什麼？當我們從右到左滑動電壓表時，它會顯示什麼？如果沒有任何電流，沿電阻器的區域性電壓是多少 - 零、10 V 還是其他什麼？

好吧，讓我們試試。首先，將萬用表的黑色測試端連線到地線。然後用紅色萬用表探針接觸電阻絲，並沿著電阻絲移動探針，測量所有電壓降（目前，相對於地線）！如果你累了，可以將鱷魚夾夾在探針上，"咬"住電阻絲，然後沿著電阻絲移動這個"滑塊"！也許，正是用這種方式，在很久以前，有人發明了真正的電位器... 無論如何，結果令人驚歎：無論鱷魚夾在電阻膜上的哪個位置，所有區域性電壓都是 10V！ 顯然，這個電氣現象與我們上面觀察到的液壓現象相同：上面：連線在開路中的電阻絲上測量的區域性電壓相同，都等於輸入電壓。但是為什麼呢？

記住電阻的作用 - 它"阻礙"。它阻礙什麼？它阻礙、阻擋、干擾電流，透過耗散功率。但在開路中沒有電流流動。因此，沒有東西需要阻礙；當沒有電流時，電阻不是電阻。只有當有東西需要阻礙時，電阻才是電阻！

我們可以用壓力圖的概念來類似地表示電阻絲上的電壓分佈。我們可以將電壓視為一種壓力；因此，我們可以用區域性電壓柱來表示區域性電壓，就像我們用區域性水柱來表示區域性壓力一樣（圖 4）！與上面一樣，電壓柱的長度與區域性電壓相對於地線的幅度成正比（我們可以將零電壓水平設定在電阻的高度，然後在電阻水平之上繪製正電壓柱，在之下繪製負電壓柱）。這些電壓柱的集合構成了整個電壓圖。以後，為了簡化影像，我們將經常使用電壓圖的包絡線來代替電壓柱的集合。

閉合電路

"發明"各種電阻器

運動到電壓轉換器。現在，將電阻絲的右端接地。但是要小心；電阻絲很熱！看電流表 - 它顯示為 1A；所以，功率為 P = V.I = V²/R = I².R = 10W。順便問一下，這些計算正確嗎（電阻值是恆定的）？我們看到，對於這根細電阻絲來說，將熱量散發到環境中太困難了，它正在發熱。

現在，再次沿電阻絲移動"鱷魚滑塊"，測量區域性電壓降；歐姆做了完全相同的事情。他將探針從一個位置移動到另一個位置，測量相應的電勢，求出它們的差，並計算比值（V₂ - V₁)/(L₂ - L₁) = (V₂ - V₁)/(r₂ - r₁) = dV/dR = I。因此，他確定這個比值（即電流 I）沿電阻絲是恆定的；因此，歐姆得出結論：V/R = I。

我們可以看到，當移動"鱷魚滑塊"時，電壓降從 10 伏逐漸減小到 0 伏；相應地，電壓圖中的柱子也會逐漸減小它們的長度（圖 5）。對於任何具有某個電阻值並傳遞大電流到功率負載的真實導體，我們都可以繪製這樣的圖。

這裡，輸入量是什麼，輸出量是什麼？歐里卡！以"滑塊"的移動作為輸入，測量電壓降作為輸出，我們就"發明"了傳說中的（但名字錯誤的）電位器、運動到電壓轉換器、感測器... 輸出量和輸入量之間的關係是什麼？我們"發明"的感測器是線性運動到電壓轉換器嗎？如果是，為什麼？提示：電阻沿電阻絲線性分佈。好吧，根據電阻沿電阻絲線性分佈這一事實，我們可以得出結論，該轉換器是線性的。

在哪些地方可以看到這樣的感測器？當然，最流行的應用是燃油箱液位感測器，其中浮子移動這樣的電阻感測器。但是，如果你有一天開啟燃油箱（小心，這很危險！），你就會發現它是非線性的。你能說出原因嗎？

雙極性運動到電壓轉換器。我們已經準備好進行更復雜的實驗... 是否還有其他有趣的點（與無處不在的地線不同）可以固定負電壓探針？當然，我們可以接觸任何電阻絲的點！一種典型的佈置是將正軌（這裡為 +10V）指定為地線。但也許最有趣的點是充當地線的中間點；所以，用黑色（負極）"鱷魚夾" "咬"住它。然後，將紅色（正極）"鱷魚夾"沿電阻絲滑動，移到黑色"鱷魚夾"的左側和右側（圖 6）。但是，首先用雙極性萬用表替換單極性萬用表。為什麼？我們能預期什麼？結果令人驚喜：輸出電壓從 -5V 變化到 +5V！歐里卡！我們獲得了一個雙極性運動到電壓感測器！當然，另一個應用是雙極性可變電壓源。

共模訊號。讓我們繼續實驗... 如果我們同時將兩個萬用表探針向同一個方向移動，會發生什麼？電壓沒有變化。為什麼？他們將這種輸入稱為"共模輸入訊號"。

差分輸入訊號。如果我們同時將兩個萬用表探針向相反方向移動，會發生什麼？電壓的變化速度甚至比上面更快。為什麼？他們將這種輸入稱為"差分輸入訊號"。

用奇特的指示器測量電壓降

我們可以使用更不尋常的指示器來測量電阻絲上的電壓降，例如電燈泡（圖 7）、電機、LED等。你覺得用這種奇特的方式（圖 8）給電燈泡供電會有什麼問題嗎？如果有，什麼時候以及為什麼？

你知道旅行用吹風機和烤麵包機利用了同樣的強大理念，用低電壓為其內部電路（電機、定時器等）供電嗎？然後，讓我們以類似的方式給一個小型的直流電機供電（圖 9）。正如我們所看到的，電機速度與其速度成正比。同樣，如果我們交換兩個鱷魚夾，電機會改變旋轉方向（圖 10）。

研究奇特的"電阻器"

鉛筆石墨。如果我們有足夠的創意，我們就可以研究各種不尋常的電阻材料，以觀察它們上的電壓分佈。例如，我們可以用普通鉛筆石墨上的部分電壓降來給各種負載（包括 LED）供電（圖 11）；這似乎是在網上非常流行的實驗。^[1]

導電泡沫。另一個非傳統但非常吸引人的實驗是研究導電泡沫中的電壓分佈（圖 12）。但是，這需要使用一個完美的萬用表（為什麼？）。但是這裡的電壓分佈是線性的還是表面的呢？

石墨軌跡。最後，如果我們用軟鉛筆在紙上畫一條電阻路徑（鉛越軟，導電性越強），然後沿著這條"電阻器"滑動萬用表探針，我們就可以在我們的實驗中走得太遠了。但你不覺得我們甚至可以測量我們人體的電壓分佈嗎？當然，對於所有這些奇特的實驗，我們需要一個非常、非常完美的（高電阻）萬用表....

如何在螢幕上視覺化電壓圖

基本思想。但是，對於我們人類來說，在電路屬性（電壓和電阻）變化時繪製所有電壓圖太難了，也太無聊了。因為這些圖不能是靜態的、死的影像；它們必須是"活的"圖（動畫），根據電路狀態發生變化。因此，我們需要一臺計算機，它能密切"觀察"我們對被測電路的操作，並在螢幕上構建相應的"活"電壓圖。然後，讓我們構建這樣一個基於計算機的系統，讓它來做這個"苦力"：）。這樣，我們只需要看螢幕上的影像，並思考它背後的電路現象就行了！

元件。首先，我們需要一些計算機。它可以足夠簡單，只要它有一些圖形功能（例如，1986 年用於在這個實驗室構建 *Microlab* 系統的計算機是著名的 Apple II 的一個版本）。然後，我們只需要將一些模擬-數字轉換器 (ADC) 連線到 PC 匯流排，它們充當模擬輸入，以及一些數字-模擬轉換器 (DAC) 充當模擬輸出，我們的基於計算機的系統 *Microlab* 就準備好了（參見圖 13）！

電源。請注意，模擬-數字外設（圖 14）直接從可憐的計算機上“吸收”能量；因此，它不僅充當計算機，還為外設供電。那麼，我們也可以為高電阻物體供電嗎？我們能使用這些 DAC 來為被測電阻供電嗎？這將允許計算機控制物體！只是，這些 DAC 的運算放大器輸出只能提供最大 10 mA 電流。因此，我們無法為低電阻（10 Ω）電線供電！

電阻器。我們可以使用線性高電阻（例如，4.7 kΩ）可變電阻來代替低電阻電線。然後，我們可以使用 DAC 的 10 mA 輸出為電阻器供電，沒有任何問題（計算最大電流）。為了使裝置更復雜，我們可以同時為電阻器兩端供電。因此，將 AO1（DAC1）連線到電阻器右側，將 AO2（DAC2）連線到電阻器左側。

電壓表。你覺得是否應該連線兩個老式但吸引人的雙極性電壓表 V1 和 V2 來觀察輸入電壓？或者只依賴於抽象的數字萬用表和螢幕上的數字測量結果？但是，這些好用的老式儀表是“活的”、移動的、幾何的、空間的和真實的；這就是人們信任它們的原因。請注意，它們也是雙極性的，中間為零。但是，它們具有 20 kΩ 的內部電阻，這會有什麼問題嗎？提示：這兩個 DAC 充當具有幾乎為零輸出電阻的完美電壓源。

接地。現在，我們也來說說接地。但是，什麼是接地？我們可以在維基百科關於虛擬接地的文章中找到可能的答案。簡而言之，接地是參考點，我們根據它測量電壓。複合電壓源內部的任何點都可以充當真實接地（圖 15）。我們使用的 PC 電源是所謂的“分體電源”。它由兩個串聯連線的 12 V 電源組成（- + >>> - +）。中間點在此配置中充當接地。這些 DAC 的接地內部連線到該接地。我們還必須將電壓表的黑色測試端連線到該接地。

軟體。現在，讓我們啟動一個程式，該程式可以將電壓圖視覺化顯示在螢幕上，作為“活的”動畫。為此，程式使計算機“關注”三個關鍵點處的區域性電壓——電阻器左側端點、滑塊中間點和右側端點。然後，讓我們透過連線來滿足它的好奇心：) 首先，將 DAC1 的輸出連線到 ADC1 的輸入，將 DAC2 的輸出連線到 ADC2 的輸入；然後，將 ADC3 的輸入連線到滑塊。我們可以使用鍵盤箭頭控制這兩個 DAC 的輸出電壓；因此，這兩個 DAC 實際上充當可程式設計電壓源。計算機持續測量三個電壓（V_IN1、V_IN2 和 V_IN3），並繪製三個電壓條，它們的長度與電壓大小成正比。最後，它使用一條代表電壓圖包絡的線將它們連線起來。

為了更真實，我們首先可以拆卸可變電阻器（“電位器”）並將測量探頭直接接觸到電阻膜。現在，我們準備繼續進行這些令人驚歎的實驗。我們將使用眾所周知的“發明”各種裝置的技術：一次只改變一個量，同時保持其他量恆定。讓我們開始吧！

改變 V1：左側控制的電壓-電壓轉換器

上面，我們保持兩個電壓恆定，同時改變（移動）滑塊位置；因此，我們“發明”了運動-電壓轉換器。但是，為什麼不改變數的角色呢？

同樣，我們可以將“鱷魚滑塊”停在某個地方（例如，電線中間），然後改變輸入電壓作為輸入，就像之前一樣，測量電壓降（相對於接地）作為輸出。因此，配置如下：我們有兩個電壓源；其中一個（現在是左側的一個）變化，另一個保持恆定。計算機螢幕上的結果（圖 16）令人驚歎——電壓圖的左端上升和下降，沿圖的所有點也以減小的幅度做相同的動作（形象地說，我們可以將電壓圖想象成二等阿基米德槓桿）。我們可以在這種幾何解釋中直接看到歐姆定律

$I_{OUT}={\frac {V_{IN1}}{r1+r2}}={\frac {V_{IN1}}{R}}$

因此，我們“發明”了最簡單的電壓-電流轉換器。但更重要的是，我們“發明”了傳奇的電壓分配器（電壓-電壓轉換器或“電位器”），它在這裡由左側控制！輸入電壓和輸出電壓之間的關係是什麼（所謂的“傳遞比”？我們可以直接從螢幕上“活”的幾何解釋（兩個巢狀的相似三角形）中推匯出它——V_OUT = V_IN1.L₂/(L₁ + L₂)。由於電阻 *r* 與長度 *L* 成正比（電阻器是線性的），我們可以得出結論

如果 V1 變化，電阻器充當左側控制的電壓-電壓轉換器，其傳遞比為 $\ Vout={\frac {r2}{r1+r2}}.Vin1$

改變 V2：右側控制的電壓-電壓轉換器

上面，我們“晃動”了電阻器（電壓圖）的左端，同時保持右端固定在零接地水平。但是，為什麼不透過“移動”右端並保持左端固定在零水平來交換角色呢？讓我們試試！

螢幕上的結果（圖 17）並不比上面遜色——現在，電壓圖的右端在晃動，沿圖的所有點也以與距離成正比的減小的幅度晃動。同樣，我們可以將電壓圖想象成二等阿基米德槓桿，我們從右側轉動它。

因此，我們獲得了另一個電壓分配器（電壓-電壓轉換器或“電位器”），它在這裡由右側控制。輸入電壓和輸出電壓之間的關係是什麼？螢幕上“活”的幾何解釋（兩個巢狀的相似三角形）將再次幫助我們——V_OUT = V_IN2.L₁/(L₁ + L₂)。因此，結論與上一個結論類似

如果 V2 變化，電阻器充當右側控制的電壓-電壓轉換器，其傳遞比為

$\ Vout={\frac {r1}{r1+r2}}.Vin2$

同時改變 V1 和 V2：電阻求和器

在之前的實驗中，當我們改變某些輸入電壓時，我們保持另一個電壓等於零。但是，如果我們將另一個電壓保持為某個（例如，正）電壓，會發生什麼？更重要的是，如果我們同時改變兩個電壓，會發生什麼？讓我們先假設它們具有相同的極性。

螢幕上的結果（圖 18）比之前的更令人驚歎——透過改變兩個電壓，我們可以將左側和右側的電壓圖抬升和下降。沿著電壓圖的區域性電壓從低電壓源逐漸減小到高電壓源。現在，我們可以將電壓圖看作一個從左側和右側同時轉動的雙面二級阿基米德槓桿。

我們現在“發明”了什麼樣的裝置？輸入電壓 V_IN1、V_IN2、滑塊位置 L₁/(L₁ + L₂) 和輸出電壓 V_OUT 之間的關係是什麼？螢幕上“存在”的迷人幾何解釋（梯形）將再次幫助我們。如您所見，梯形的兩條平行邊代表兩個輸入電壓；內部線段代表輸出電壓。您可能可以解決這個常見的幾何學校問題（提示：畫一條輔助對角線）——V_OUT = V_IN1.L₂/(L₁ + L₂) + V_IN2.L₁/(L₁ + L₂)。因此，結論與之前的結論類似。

如果兩個輸入電壓都發生變化，則電阻器充當具有傳輸比的無源電阻夏季。

$\ Vout=\ {\frac {r2}{r1+r2}}.Vin1\ +{\frac {r1}{r1+r2}}.Vin2$

但這並非一個簡單的夏季；如我們所見，這是一個帶有加權係數的夏季。

$\ a={\frac {r2}{r1+r2}}$ 和 $\ b={\frac {r1}{r1+r2}}$

建立虛擬接地

無源電阻減法器

我們終於到達了故事中最有趣的部分……在之前的實驗中，我們使用了極性相同的兩個電壓。但是為什麼不反轉一個輸入源的極性呢？讓我們試試吧！

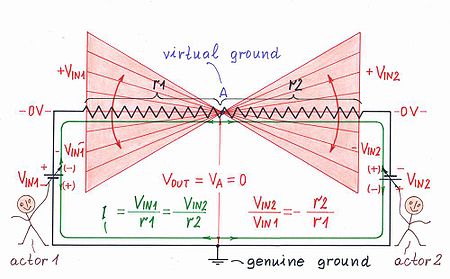
螢幕上的結果（圖 19）令人驚訝且驚歎——一個電壓 V_A = 0（相對於地）為零的點 A 出現在電阻膜上的某個位置！請注意，這個神秘點沒有連線到真實（真實、真正的）地，但它的行為卻像這樣的地！這是一種人工的，虛擬接地……通常，他們在解釋運算放大器電路時會介紹這個概念。但我們可以看到，這不是運算放大器電路的獨特屬性；它是這個只包含兩個電阻的簡單電阻電路的屬性。從這個角度看，歐姆早在 1826 年就可能觀察到虛擬接地現象，如果他只引入了一個第二個電壓源！

再次，螢幕上“存在”的迷人幾何解釋（兩個相似但現在相反的三角形）將幫助我們制定在給定點存在虛擬接地的要求。顯然，兩個輸入電壓 V_IN1 和 V_IN2 必須具有相反的極性，並且它們必須與相應的電阻 r1 和 r2（R₁ 和 R₂，如果它們代表單獨的電阻）之間的比例相同： ${\frac {V_{IN2}}{V_{IN1}}}=-{\frac {r_{2}}{r_{1}}}$

如果您喜歡類比，您可以將這種安排視為一個電氣“拔河”，兩個電壓源“相互對抗”——V_IN1“向上拉”點 A，而 V_IN2“向下拉”點 A。上拉電阻 r1 和下拉電阻 r2 在這裡充當電氣“繩索”。

負反饋遊戲

如果我們開始改變輸入電壓 V_IN1 或 V_IN2 或兩個電壓（保持 V_IN1 = -V_IN2），會發生什麼？看看，虛擬接地點左右移動！我們能把它停在電阻膜上的某個地方嗎？如果我們設法把它停下來，我們將能夠建立著名的帶負反饋的電路……讓我們試試吧！

您是否認為，與其進行枯燥的實驗，不如玩一個有趣的遊戲來模仿負反饋系統？如果您同意這個建議，讓我們來分配角色:) 我們中的一人（“演員”1）可以扮演（成為、控制）主要獨立輸入電壓源 V_IN1。另一個“演員”2 可以代表第二個依賴電壓源 V_IN2；他/她必須保持虛擬接地不動。為此，他/她只需觀察虛擬接地點（一個零指示器可能有助於測量其電壓）並改變 V_IN2，以使虛擬接地電壓始終等於零。

螢幕上的結果（圖 20）簡直太棒了！演員 1 (V_IN1) 試圖移動虛擬接地點，但演員 2 (V_IN2) 將其返回到舊位置。電壓圖圍繞固定虛擬接地點旋轉，V_IN2 始終與 V_IN1 成比例；第二個電壓以相反極性跟隨第一個電壓： $V_{IN2}=-{\frac {r_{2}}{r_{1}}}V_{IN1}$ .

真是個好主意！實際上，我們可以將輸入電壓 V_IN2 視為一個輸出電壓，並且我們可以真正地將其用作輸出電壓！這種安排代表了帶負反饋的最簡單的反相系統。

運算放大器反相放大器

如我們所見，演員 2 對這種“苦力”感到厭倦了——觀察虛擬接地並改變 V_IN2:) 還有什麼可以做嗎？運算放大器似乎是一個不錯的選擇（圖 21）。它具有完美的電氣感；因此，它不需要零指示器來監測虛擬接地電壓。同樣，如果演員 1 也感到厭倦了，我們可以讓計算機在 DAC1 的輸出端產生一個週期性電壓。好吧，我們可以看到運算放大器在數量之間保持與上述相同的比例： $V_{OA}=-{\frac {R_{2}}{R_{1}}}V_{IN}$ ；因此，我們“發明”了著名的運算放大器反相放大器！現在，我們可以透過改變滑塊的位置進行一些實驗：在中點，在中點的左側和右側。運算放大器如何對這種“干預”做出反應？電壓圖會發生什麼變化？我們可以利用所有這些情況來構建電子電路嗎？

另請參見

直流電路中的電壓降
 構建並聯電壓求和器使用更基本的電路構建模組
虛擬接地揭示了這一著名現象的秘密

參考文獻

↑ 電位器作為分壓器由 Tony Kuphaldt 展示了用鉛筆石墨進行有趣實驗

外部連結

紙質電路 (YouTube 影片)
具有電壓輸出的複合無源轉換器
並聯電壓求和器透過使用更簡單的電壓到電流和電流到電壓轉換器來構建電路 (Flash 動畫；需要 Ruffle 擴充套件）。
我們如何建立一個虛擬接地？是關於這一偉大現象的電路故事。

<<< 頂部 - 目錄 - 頁面階段 >>>

[1] 電位器作為分壓器由 Tony Kuphaldt 展示了用鉛筆石墨進行有趣實驗