電路理論/分析方法

電路理論

分析方法

當電路變得龐大而複雜時，擁有各種簡化和分析電路的方法將非常有用。沒有完美的公式來解決電路問題。根據電路的型別，可以採用不同的方法來解決電路。某些方法可能無效，而某些方法在涉及複雜數學運算時可能非常困難。解決電路的兩個最重要方法是節點分析法和網孔電流分析法。這些方法將在下面進行解釋。

疊加

電路分析領域最重要的原則之一是疊加原則。它僅對線性電路有效。

疊加原理指出，多個貢獻源對線性電路的總效應等於每個源單獨作用時的效應之和。

這意味著什麼？用通俗的語言來說，這意味著如果我們有一個具有多個源的電路，我們可以一次“關閉”除一個源之外的所有源，然後僅用一個源啟用的情況下研究電路。我們對每個源依次進行此操作，然後將每個源的效應加在一起得到總效應。在我們使用此原理之前，我們必須瞭解其背後的數學基礎。

必要條件

疊加只能應用於線性電路；也就是說，電路中所有源與電路響應之間都存線上性關係。僅使用幾個代數規則，我們可以構建疊加的數學理解。如果f表示響應，a和b是常數，那麼

f(ax_{1}+bx_{2})=f(ax_{1})+f(bx_{2})\,

就電路而言，它清楚地解釋了疊加的概念；每個輸入可以單獨考慮，然後相加得到輸出。通過幾個額外的代數性質，我們可以看到疊加不能應用於非線性電路。在這個例子中，響應y等於輸入x的平方，即 y=x²。如果a和b是常數，那麼

y=(ax_{1}+bx_{2})^{2}\neq (ax_{1})^{2}+(bx_{2})^{2}=y_{1}+y_{2}\,

請注意，這只是無限多個反例之一……

逐步操作

使用疊加法來找到給定的輸出可以分解為四個步驟

隔離一個源 - 選擇一個源，並將所有剩餘的源設定為零。在開路和閉路電路中解釋了“關閉”這些源的後果。總而言之，關閉電壓源會導致短路，關閉電流源會導致開路。（原因 - 無法透過開路流動電流，短路之間沒有壓降。）
找到來自隔離源的輸出 - 一旦隔離了一個源，可以使用我們到目前為止學習的任何技術來找到該源的響應。
對每個源重複步驟1和2 - 繼續選擇一個源，將剩餘的源設定為零，然後找到響應。重複此過程，直到考慮了所有源。
將輸出相加 - 一旦找到每個源導致的輸出，將它們加在一起即可找到總響應。

衝激響應

可以利用電路的衝激響應來確定電路的輸出。

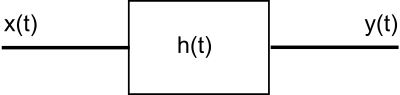
輸出 y 是輸入 x 與衝激響應的卷積 h * x。

[卷積]

y(t)=(h*x)(t)=\int _{-\infty }^{+\infty }h(t-s)x(s)ds

.

如果輸入 x(t) 是衝激 ( $\delta (t)$ )，輸出 y(t) 將等於 h(t)。

通過了解電路的衝激響應，可以將任何源插入電路，然後透過卷積計算輸出。

卷積

卷積運算是一個非常困難且複雜的運算，它將兩個方程組合成一個結果方程。卷積的定義基於定積分，因此求解卷積方程需要積分微積分的知識。本華夏公益教科書不需要讀者事先了解積分微積分，因此不會深入討論這個主題，只提供簡單的定義和一些解釋。

定義

兩個函式 a 和 b 的卷積 a * b 定義為

(a*b)(t)=\int _{-\infty }^{\infty }a(\tau )b(t-\tau )d\tau

記住
星號表示卷積，而不是乘法

星號運算子用於表示卷積。許多計算機系統和經常在計算機上寫數學的人通常使用星號表示簡單的乘法（星號是許多程式語言中的乘法運算子），但在這裡必須做出重要的區分：星號運算子表示卷積。

性質

卷積是可交換的，也就是說 $a*b=b*a$ 。卷積也對加法是分配的，即 $a*(b+c)=a*b+a*c$ ，並且是結合的，即 $a*(b*c)=(a*b)*c$ .

系統和卷積

假設我們有以下的框圖系統

	x(t) = 系統輸入 h(t) = 衝激響應 y(t) = 系統輸出

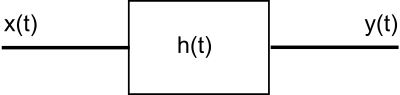其中 x(t) 是電路的輸入，h(t) 是電路的衝激響應，y(t) 是輸出。在這裡，我們可以透過將衝激響應與電路的輸入進行卷積來找到輸出。因此，我們看到電路的衝激響應不僅僅是輸出與輸入的比率。然而，在頻域中，輸出中頻率為 ω 的分量是輸入中具有相同頻率的分量與該頻率下傳遞函式的乘積。故事的寓意是：電路的輸出是輸入與衝激響應的卷積。