電路理論/拉普拉斯變換

拉普拉斯變換

拉普拉斯變換是一種強大的工具，在電氣工程中非常有用。該變換允許將“時域”中的方程轉換為複數 s 域中等效的方程。拉普拉斯變換是一種積分變換，雖然讀者不需要了解積分微積分，因為所有結果都將提供。本頁面將討論拉普拉斯變換，它只是一種用於求解和操作常微分方程的工具。

電路元件的拉普拉斯變換類似於相量表示，但它們並不相同。拉普拉斯變換比相量更通用，並且在某些情況下更容易使用。此外，不要將“複數 s 域”與我們之前討論過的復功率概念混淆。復功率使用變數$\mathbb {S}$，而拉普拉斯變換使用變數 s。拉普拉斯變數 s 與功率無關。

該變換以數學家皮埃爾·西蒙·拉普拉斯（1749-1827）的名字命名。該變換本身直到奧利弗·亥維賽德，一位著名的電氣工程師，開始使用它的變體來求解電路才變得流行。

拉普拉斯域

拉普拉斯域，或“複數 s 域”，是拉普拉斯變換將時域方程變換到的域。s 是一個復變數，由實部和虛部組成

$s=\sigma +j\omega$

拉普拉斯域將實部 (σ) 作為橫軸，將虛部 (ω) 作為縱軸。s 的實部和虛部可以被視為獨立量。

此符號與傅立葉變換理論中使用的符號的相似之處並非巧合；對於$\sigma =0$，如果訊號是因果的，則拉普拉斯變換與傅立葉變換相同。

變換

拉普拉斯變換的數學定義如下

[拉普拉斯變換]

$F(s)={\mathcal {L}}\left\{f(t)\right\}=\int _{0^{-}}^{\infty }e^{-st}f(t)\,dt$

注意
字母s沒有特殊含義，在拉普拉斯變換中使用它是作為一種常見約定。

變換，透過定積分，消除了結果方程中的所有 t，而是留下新的變數 s，它是一個複數，通常寫成$s=\sigma +j\omega$。本質上，該變換取函式 f(t)，並將其“變換”為關於 s 的函式 F(s)。一般來說，函式 f(t) 的變換寫成 F(s)。時域函式用小寫字母表示，而結果的 s 域函式用大寫字母表示。

在
附錄中

有一個拉普拉斯變換對的表格，我們將使用以下符號來顯示函式的變換

$f(t)\Leftrightarrow F(s)$

我們使用這種符號，因為我們可以使用拉普拉斯逆變換將 F(s) 轉換回 f(t)。

逆變換

拉普拉斯逆變換將複數 S 域中的函式轉換為其在時域中的對應函式。它的數學定義如下

[拉普拉斯逆變換]

${\mathcal {L}}^{-1}\left\{F(s)\right\}={1 \over {2\pi }}\int _{c-i\infty }^{c+i\infty }e^{ft}F(s)\,ds=f(t)$

其中 $c$ 是一個實常數，使得所有極點 $s_{1},s_{2},...,s_{n}$ of $F(s)$ 位於區域 ${\mathfrak {R}}\{s_{i}\}<c$ 中。換句話說，$c$ 的選擇使得 $F(s)$ 的所有極點都在與實軸在 $s=c$ 處相交的垂直線左側。

逆變換在數學上比變換本身更困難。然而，幸運的是，拉普拉斯變換及其逆變換的廣泛表格已經計算出來，並且可以方便地瀏覽。

變換性質

拉普拉斯變換性質表在
附錄

拉普拉斯變換最重要的性質（目前）如下

${\mathcal {L}}\left\{f'(t)\right\}=sF(s)-f(0)$

類似地，我們可以用類似的方式表達高階導數

${\mathcal {L}}\left\{f''(t)\right\}=s^{2}F(s)-sf(0)-f'(0)$

或者對於任意導數

${\mathcal {L}}\left\{f^{(n)}(t)\right\}=s^{n}F(s)-\sum _{i=0}^{n-1}s^{(n-1-i)}f^{(i)}(0)$

其中符號 $f^{(n)}(t)$ 表示函式 $f$ 在點 $t$ 處的 n 次導數，而 $f^{(0)}(t)$ 表示 $f(t)$.

通俗地說，拉普拉斯變換將微分運算轉化為多項式運算。唯一需要記住的重要一點是，我們必須新增時域函式的初始條件，但對於大多數電路，初始條件為 0，因此我們不需要新增任何東西。

對於積分，我們得到以下結果

${\mathcal {L}}\left\{\int _{0}^{t}f(t)\,dt\right\}={1 \over s}F(s)$

初始值定理

拉普拉斯變換的**初始值定理**如下所示：

[初始值定理]

$f(0)\Leftrightarrow \lim _{s\to \infty }sF(s)$

這對於求解微分運算變換時所需的函式初始條件很有用（見上文）。

最終值定理

與初始值定理類似，**最終值定理**指出，我們可以找到函式 f 在 t 趨於無窮大時的值，在拉普拉斯域中，如下所示：

[最終值定理]

$\lim _{t\to \infty }f(t)\Leftrightarrow \lim _{s\to 0}sF(s)$

這對於求解電路的穩態響應很有用。最終值定理只能應用於穩定系統。

傳遞函式

如果我們有一個在時域中具有脈衝響應 h(t) 的電路，輸入為 x(t)，輸出為 y(t)，我們可以透過變換所有三個元素來找到電路在拉普拉斯域中的**傳遞函式**。

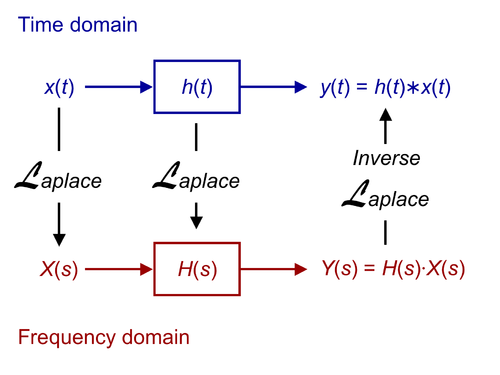
在這種情況下，H(s) 被稱為電路的“傳遞函式”。它可以定義為脈衝響應的變換，也可以定義為電路輸出與其在拉普拉斯域中的輸入的比值。

[傳遞函式]

$H(s)={\mathcal {L}}\left\{h(t)\right\}={\frac {Y(s)}{X(s)}}$

傳遞函式是分析電路的強大工具。如果我們知道電路的傳遞函式，那麼我們就掌握了理解電路所需的所有資訊，而且我們擁有了一種易於操作的形式。當我們獲得傳遞函式時，就可以說電路已完全“解決”。

卷積定理

之前提到過，我們可以透過使用卷積運算來計算系統的輸出，該輸出來自輸入和脈衝響應。作為提醒，給定以下系統：

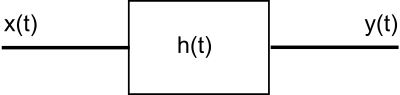
x(t) = 系統輸入 h(t) = 脈衝響應 y(t) = 系統輸出

我們可以使用卷積運算來計算輸出，如下所示：

$y(t)=x(t)*h(t)$

其中星號表示卷積，而不是乘法。但是，在 S 域中，由於拉普拉斯變換的一個特性，此運算變得容易得多。

[卷積定理]

${\mathcal {L}}\left\{a(t)*b(t)\right\}=A(s)B(s)$

其中星號運算子表示卷積運算。這使我們得到了卷積定理的英文表述：

時域中的卷積在 S 域中變為乘法，S 域中的卷積在時域中變為乘法。

現在，如果我們在拉普拉斯 S 域中有一個系統

X(s) = 輸入 H(s) = 傳遞函式 Y(s) = 輸出

我們可以從輸入 X(s) 和傳遞函式 H(s) 計算輸出 Y(s)

$Y(s)=X(s)H(s)$

注意，此屬性與相量非常相似，其中可以透過將輸入乘以網路函式來確定輸出。因此，網路函式和傳遞函式是非常相似的量。

電阻

拉普拉斯變換可以獨立地應用於不同的電路元件，然後可以在 S 域中完全求解電路（這更容易）。讓我們看看一些電路元件

電阻是時間和頻率不變的。因此，電阻的變換與電阻本身的阻值相同

[電阻變換]

$R(s)=r$

將此結果與電阻 r 的相量阻抗值進行比較

$Z_{r}=r\angle 0$

您可以很快地看到，相量和拉普拉斯變換之間的阻值非常相似。

歐姆定律

如果我們將歐姆定律進行變換，我們將得到以下方程式

[歐姆定律變換]

$V(s)=I(s)R$

現在，根據歐姆定律，電路元件的電阻是電壓與電流的比值。因此，我們將求解量 ${\frac {V(s)}{I(s)}}$，結果將是我們的電路元件的電阻

$R={\frac {V(s)}{I(s)}}$

這個比值，即電阻的輸入/輸出比值，是一個重要的量，我們將為所有電路元件找到這個量。我們可以說，阻值為 r 的電阻的變換由下式給出

[電阻變換]

${\mathcal {L}}\{{\text{resistor}}\}=R=r$

電容器

讓我們看一下時間域中電壓、電流和電容之間的關係

$i(t)=C{\frac {dv(t)}{dt}}$

求解電壓，我們得到以下積分

$v(t)={\frac {1}{C}}\int _{t_{0}}^{\infty }i(t)dt$

然後，將這個方程變換到拉普拉斯域，我們得到以下結果

$V(s)={\frac {1}{C}}{\frac {1}{s}}I(s)$

同樣，如果我們求解比值 ${\frac {V(s)}{I(s)}}$，我們將得到以下結果

${\frac {V(s)}{I(s)}}={\frac {1}{sC}}$

因此，電容為 C 的電容器的變換由下式給出

[電容器變換]

${\mathcal {L}}\{{\mbox{capacitor}}\}={\frac {1}{sC}}$

電感器

讓我們看看電感的方程式

$v(t)=L{\frac {di(t)}{dt}}$

將其代入拉普拉斯域，我們得到以下公式

$V(s)=sLI(s)$

求解比值 ${\frac {V(s)}{I(s)}}$，我們得到以下結果

${\frac {V(s)}{I(s)}}=sL$

因此，電感為 L 的電感器的變換由以下給出

[電感器的變換]

${\mathcal {L}}\{{\text{inductor}}\}=sL$

阻抗

由於所有負載元件可以合併成一個依賴於 s 的單一格式，因此我們將所有負載元件的效果稱為阻抗，與我們在相量表示中所稱的一樣。我們用大寫字母 Z 表示阻抗值（但不表示相量 $\mathbb {Z}$）。

確定電路中的電流

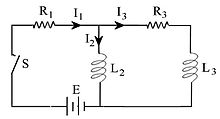電容為零、初始電流為零的 RCL 電路。

在所示網路中，假設每個電流在開關閉合時均為零，確定電流 $I_{1}(t)$、$I_{2}(t)$ 和 $I_{3}(t)$ 的性質。

解

電路中結點的電流流動

由於任何結點處電流的代數和為零，因此

$I_{1}(t)-I_{2}(t)-I_{3}(t)=0$.........(182)

電路上的電壓平衡

將電壓定律應用於左側的電路，我們得到

$I_{1}(t)R_{1}+L_{2}{\frac {dI_{2}(t)}{dt}}\ =E(t)$......... (182-1)

再次將電壓定律應用於外部電路，考慮到 E 是恆定的，我們得到

$I_{1}(t)R_{1}+I_{3}(t)R_{3}+L_{3}{\frac {dI_{3}(t)}{dt}}\ =E(t)$......... (182-2)

電流和電壓方程的拉普拉斯變換

對 (182)、(182-1) 和 (182-2) 進行拉普拉斯變換，我們得到

$i_{1}(s)-i_{2}(s)-i_{3}(s)=0$.........(182-3)

$i_{1}(s)R_{1}+sL_{2}i_{2}(s)={\frac {E}{s}}\$......... (182-4)

$i_{1}(s)R_{1}+(R_{3}+sL_{3})i_{3}(s)={\frac {E}{s}}\$ ......... (182-5)

拉普拉斯變換的實現回顧

三個拉普拉斯變換後的方程 (182-3)、(182-4) 和 (182-5) 展示了 積分變換將微分方程轉換為線性代數方程的優勢，可以求解這些方程以獲得因變數（在本例中為三個電流），然後進行逆變換以得到所需的解。

• 在方程 (182-3) 中，我們利用了拉普拉斯變換的 *求和性質*。
• 在方程 (182-4) 中，我們利用了 *微分導數* 的變換，如下所示。

$si_{2}(s)-I_{2}(0)={\mathcal {L}}\left\lbrace {\frac {dI_{2}}{dt}}\right\rbrace$.........(182-4.1)

由於給定的初始條件替代為：$I_{2}(0)=0$

• 在方程 (182-5) 中，我們也利用了微分導數的變換

$si_{3}(s)-I_{3}(0)={\mathcal {L}}\left\lbrace {\frac {dI_{3}}{dt}}\right\rbrace$.........(182-5.2)

同樣，我們用給定的初始條件替代：$I_{3}(0)=0$

施加的電壓是階躍函式這一事實表明使用了階躍函式的拉普拉斯變換，如下所示

${\frac {E}{s}}={\mathcal {L}}\left\lbrace E\right\rbrace$.........(182-5.3)

求解線性聯立方程

三個線性聯立方程（182-3）、（182-4）和（182-5）有三個未知數 $i_{1}(s)$，$i_{2}(s)$和$i_{3}(s)$，可以透過克萊姆法則等簡單的消元方法求解，如下。

$i_{1}(s)={\frac {\begin{vmatrix}0&-1&-1\\{\frac {E}{s}}\ &sL_{2}&0\\{\frac {E}{s}}\ &0&R_{3}+sL_{3}\\\end{vmatrix}}{\Delta }}={\frac {E}{s}}{\frac {R_{3}+s(L_{2}+L_{3})}{\Delta }}$ ......... (182-6)

其中，矩陣的行列式 ∆ 如下確定

$\Delta ={\begin{vmatrix}1&-1&-1\\R_{1}&sL_{2}&0\\R_{1}&0&R_{3}+sL_{3}\\\end{vmatrix}}={\begin{vmatrix}1&0&0\\R_{1}&sL_{2}+R_{1}&R_{1}\\R_{1}&R_{1}&R_{1}+R_{3}+sL_{3}\\\end{vmatrix}}$

$\Delta =s^{2}L_{2}L_{3}+s(R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3})+R_{1}R_{3}$......... (182-6.1)

由於我們對 ∆ 的因式感興趣，我們考慮方程 ∆ = 0。由於這個方程的所有係數都是正數，因此它不可能有正根。它的判別式為

$(R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3})^{2}-4L_{2}L_{3}R_{1}R_{3}$ ........ (182-6.1.1)

可以寫成

$R_{1}^{2}L_{2}^{2}+2R_{1}L_{2}(R_{3}L_{2}+R_{1}L_{3})+(R_{3}L_{2}-R_{1}L_{3})^{2}$........ (182-6.1.2)

這是一個正數。因此方程 Δ = 0 具有兩個不同的負根 $-\alpha _{1}$ 和 $-\alpha _{2}$，假設。

因此，

$\Delta =L_{2}L_{3}(s+\alpha _{1})(s+\alpha _{2})$ ......... (182-6.2)

其中，$-\alpha _{1}$ 和 $-\alpha _{2}$ 是二次方程 (182-6.1) 的根，如下所示：

$\alpha _{1}={\frac {1}{2}}\left\lbrace {\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}+{\sqrt {\left({\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}\right)^{2}-4{\frac {R_{1}R_{3}}{L_{2}L_{3}}}}}\right\rbrace$ ......... (182-6.2.1)

$\alpha _{2}={\frac {1}{2}}\left\lbrace {\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}-{\sqrt {\left({\frac {R_{1}L_{2}+R_{3}L_{2}+R_{1}R_{3}}{L_{2}L_{3}}}\right)^{2}-4{\frac {R_{1}R_{3}}{L_{2}L_{3}}}}}\right\rbrace$ ......... (182-6.2.2)

因此，方程 (182-6) 和 (186-6.2) 給出

$i_{1}(s)={\frac {E}{s}}.{\frac {R_{3}+s(L_{2}+L_{3})}{L_{2}L_{3}(s+\alpha _{1})(s+\alpha _{2})}}$

$i_{1}(s)={\frac {A_{0}}{s}}+{\frac {A_{1}}{s+\alpha _{1}}}+{\frac {A_{1}}{s+\alpha _{2}}}$ .........(182-7)

常數 $A_{0}$, $A_{1}$, 和 $A_{2}$ 是用 $R_{1}$, $L_{2}$, $L_{3}$, 和 $R_{3}$ 表示的，給出如下：

$A_{0}=-{\frac {ER_{3}}{L_{2}L_{3}\alpha _{1}\alpha _{2}}}$ .........(182-7.1)

$A_{1}=E{\frac {R_{3}\alpha _{2}-\alpha _{1}\alpha _{2}(L_{2}+L_{3})}{L_{2}L_{3}\alpha _{1}\alpha _{2}(\alpha _{1}-\alpha _{2})}}$.........(182-7.2)

$A_{2}=E{\frac {\alpha _{2}(L_{2}+L_{3})-R_{3}}{L_{2}L_{3}\alpha _{2}(\alpha _{1}-\alpha _{2})}}$.........(182-7.3)

電流方程的拉普拉斯逆變換

因此，(182-7) 的拉普拉斯逆變換為：

$I_{1}(t)={\mathcal {L}}^{-1}\left\lbrace {\frac {A_{0}}{s}}+{\frac {A_{1}}{s+\alpha _{1}}}+{\frac {A_{1}}{s+\alpha _{2}}}\right\rbrace =A_{0}+A_{1}e^{-\alpha _{1}t}+A_{2}e^{-\alpha _{2}t}$.........(182-8)

剩餘變數 $I_{2}(t)$ 和 $I_{3}(t)$ 以及相應的電壓由公式 (182)、(182-1) 和 (182-2) 確定。

電路動態分析

公式 (182-8) 中的電流 $I_{1}(t)$ 顯示了一個與時間無關的成分 $A_{0}$ 以及兩個衰減項，當 t 趨於 ∞ 時，這兩個衰減項將達到漸近值。換句話說，三個電路中的電流沒有正弦振盪，主要是因為：（1）施加的電壓是恆定的，（2）電路沒有電容元件。

注意： 此示例可以透過多種方式 修改，使其涉及電壓脈衝、正弦電壓源、電容以及電荷和電流的各種邊界和初始條件。

方法的推廣

在上面的例子中，可以做以下修改

(1) 基爾霍夫方程中施加的電壓可以採用多種形式，例如

• :$E(t)=E_{o}\delta (t)$
• :$E(t)=E_{o}\sin(\omega t)$
• :$E(t)=E_{o}f(t)$

(2) 電容在持續時間內新增電流的積分項，如

• : ${\frac {1}{C}}\int _{0}^{t}I(\tau )d\tau$