電路理論/最大功率傳輸

最大功率傳輸

我們通常希望儘可能多地將源的能量傳輸到其終端上的負載。我們如何確定負載的最佳電阻以實現這一點？

讓我們考慮一個由戴維南等效電路建模的電源（諾頓等效電路將得出相同的結果，因為兩者是直接等效的），並帶有一個負載電阻R_L。源電阻為R_s，源的開路電壓為v_s。

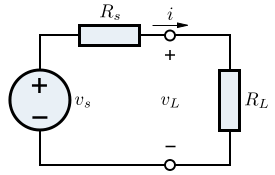
該電路中的電流可以使用歐姆定律計算

$i={\frac {v_{s}}{R_{s}+R_{L}}}$

負載電阻兩端的電壓v_L可以使用分壓器規則計算

$v_{L}=v_{s}\,{\frac {R_{L}}{R_{s}+R_{L}}}$

現在我們可以找到負載中消耗的功率P_L，如下所示

$P_{L}=v_{L}i={\frac {R_{L}\,v_{s}^{2}}{\left(R_{s}+R_{L}\right)^{2}}}$

現在我們可以改寫這個公式以消除頂部的R_L

$P_{L}={\frac {v_{s}^{2}}{\left({\frac {R_{s}}{\sqrt {R_{L}}}}+{\sqrt {R_{L}}}\right)^{2}}}={\frac {v_{s}^{2}}{R_{s}\left({\frac {\sqrt {R_{s}}}{\sqrt {R_{L}}}}+{\frac {\sqrt {R_{L}}}{\sqrt {R_{s}}}}\right)^{2}}}$

假設源電阻不可變，那麼我們可以透過最小化上述公式分母中的括號部分來獲得最大功率。這是一個基本數學結果，即$x+x^{-1}$ 當x=1時，達到最小值。在這種情況下，它等於 2。因此，上述公式在以下條件下達到最小值

${\frac {\sqrt {R_{s}}}{\sqrt {R_{L}}}}=1$

這導致了以下條件

$R_{L}=R_{s}\,$

如果負載電阻與源內部電阻相同，我們將從源中獲得最大功率。這就是最大功率傳輸定理。

效率

效率η是指電路中所有消耗的能量中消耗在負載上的比例。我們可以立即看到，在最大功率傳輸到負載的情況下，效率為 0.5，因為源電阻兩端的電壓是其一半。我們還可以看到，效率會隨著負載電阻的增加而增加，即使傳輸的功率會下降。

效率可以使用以下公式計算

$\eta ={\frac {P_{L}}{P_{L}+P_{s}}}$

其中P_s是源電阻中的功率。這可以透過對P_L公式進行簡單的修改來找到

$P_{s}={\frac {v_{s}^{2}}{R_{L}\left({\frac {\sqrt {R_{s}}}{\sqrt {R_{L}}}}+{\frac {\sqrt {R_{L}}}{\sqrt {R_{s}}}}\right)^{2}}}$

下圖展示了負載功率（佔最大功率 *P_max* 的比例）和效率，負載電阻 *R_L* 的取值範圍是源電阻 *R_s* 的 0 到 5 倍。

需要注意的是，在最大功率傳輸條件下，源端和負載端消耗的功率相等。如果電源是電力供應系統，負載是你的電加熱器，這種情況並不理想。這意味著電力供應公司會浪費掉一半的電力。在這種情況下，發電機、輸電線路等被設計成具有儘可能低的源電阻，以達到更高的效率。最大功率傳輸條件通常應用於（通常是高頻）通訊系統中，其中源電阻無法降低，功率水平相對較低，而且將盡可能多的訊號功率傳輸到系統的接收端（負載）至關重要。