電路理論/網孔分析

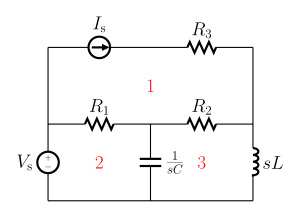
平面電路的非平凡網孔標記為 1、2 和 3。

網孔分析在相量域中進行。

網孔分析方法減少了電路中需要求解的方程和未知數的數量。

基爾霍夫方法求解所有電流和電壓。網孔分析僅求解網孔（迴路）電流。

網孔分析從普通的基爾霍夫迴路方程開始

$\Delta _{k=1}^{n}{V}_{k}=0$

並求解端子方程，使電壓成為電流的函式，然後代入迴路電壓方程

$v=\Delta I*R$

$v={\frac {\Delta I}{C*j\omega }}={\frac {\Delta I}{sC}}$

$v=\Delta I*j\omega L=\Delta I*sL$

$\Delta I$是什麼？它是可能穿過器件的兩個網孔電流之間的差（或和）。如果器件不是兩個網孔的一部分，則它可能只是一個電流。屬於兩個網孔的器件需要將網孔電流相加或相減（取決於方向）。

$\Delta I=I_{meshA}-I_{meshB}$

乍一看，網孔分析似乎很簡單，但在解決問題時，與基爾霍夫方法相比，存在細微的差別。

網孔電流可以透過同一個器件，方向相同或相反。它們不是基爾霍夫方法中單個器件的電流。如果沒有在平面電路圖上仔細標記網孔電流的方向，就無法保持方向的正確性。

• 如果網孔電流與正在編寫的特定基爾霍夫迴路方程的方向相同，則為正，如果導致負電壓，則為負。
• 網孔電流通常為順時針方向，並決定迴路方程的方向。
• 必須在相量域中進行，以便能夠計算節點之間的阻抗。
• 可能方程太少，需要從“超網孔”中找到額外的方程。
• 有些問題無法解決。識別這些問題並非易事。

網孔電流

圖 2：網孔電流標記為 i₁、i₂ 和 i₃ 的電路。箭頭顯示網孔電流的方向。

網孔分析透過在非平凡迴路/網孔中任意分配網孔電流來工作。圖 1 使用 1、2 和 3 標記了基本網孔。

網孔電流可能與任何實際流動的電流不對應，但實際電流很容易從它們中找到。通常的做法是讓所有網孔電流都沿相同方向迴圈。

示例

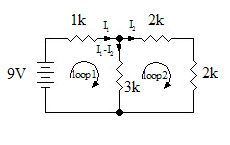用於網孔電流示例問題的電路圖。

該電路有 2 個在圖上所示的迴路。使用 KVL 我們得到

• 迴路 1： $0=9-1000I_{1}-3000(I_{1}-I_{2})$
• 迴路 2： $0=3000(I_{1}-I_{2})-2000I_{2}-2000I_{2}$

簡化後，我們得到聯立方程

$0=9-4000I_{1}+3000I_{2}$

$0=0+3000I_{1}-7000I_{2}$

求解得到

$I_{1}=3.32mA$

$I_{2}=1.42mA$

建立方程

每個網孔產生一個方程。這些方程是網孔電流完整迴路中電壓降的總和。對於比包含電流源和電壓源更一般的電路問題，電壓降將是電子元件的阻抗乘以該回路中的網孔電流。

如果網孔迴路中存在電壓源，則電壓源的電壓根據其是網孔電流方向上的電壓降還是電壓升高而加或減。對於不在兩個網孔之間包含的電流源，網孔電流將取電流源的正值或負值，具體取決於網孔電流與電流源的方向相同還是相反。以下是上面相同的電路，以及求解電路中所有電流所需的方程。

${\begin{cases}{\text{Mesh 1: }}I_{1}=I_{s}\\{\text{Mesh 2: }}-V_{s}+R_{1}(I_{2}-I_{1})+{\frac {1}{sc}}(I_{2}-I_{3})=0\\{\text{Mesh 3: }}{\frac {1}{sc}}(I_{3}-I_{2})+R_{2}(I_{3}-I_{1})+LsI_{3}=0\\\end{cases}}\,$

超級網孔

圖3：包含超級網孔的電路。超級網孔的出現是因為電流源位於基本網孔之間。

當電流源包含在兩個基本網孔之間時，就會出現超級網孔。首先將電路視為電流源不存在。這會導致一個包含兩個網孔電流的方程。一旦形成此方程，就需要一個方程將兩個網孔電流與電流源關聯起來。這將是一個電流源等於其中一個網孔電流減去另一個網孔電流的方程。以下是如何處理超級網孔的一個簡單示例。

${\begin{cases}{\text{Mesh 1, 2: }}-V_{s}+R_{1}I_{1}+R_{2}I_{2}=0\\{\text{Current source: }}I_{s}=I_{2}-I_{1}\end{cases}}\,$