節點分析是在相量域中進行的。
節點分析方法減少了電路中需要求解的方程和未知量。
基爾霍夫方法找到所有電流和電壓。節點分析只找到節點(連線點)的電壓。
節點分析從基爾霍夫節點方程開始

並求解終端方程,使電流成為電壓的函式,然後代入節點電流方程



什麼是  ? 它是在所考慮器件兩側節點相對於地面的電壓。
? 它是在所考慮器件兩側節點相對於地面的電壓。

其中電流從 node_A 流向 node_B。
乍一看這可能看起來很瑣碎,但在做問題時會暴露出一些細微的差異
- 節點電壓是相對於地面的。它們不是基爾霍夫在單個器件上的壓降。
- 假設所有電流都離開節點。
- 終端關係方程更復雜。
- 必須在相量域中進行,以便計算節點之間的阻抗。
- 可能方程太少,需要找到“超級節點”方程。
- 有些問題無法解決。識別這些並不容易。
 具有一個未知電壓 V1 的基本示例電路。
具有一個未知電壓 V1 的基本示例電路。
此電路中唯一的未知電壓是 V1。有三個連線到該節點,因此需要考慮三個電流。計算中電流方向選擇為遠離節點。
- 透過電阻 R1 的電流: (V1 - VS) / R1
- 透過電阻 R2 的電流: V1 / R2
- 透過電流源 IS 的電流: -IS
根據基爾霍夫電流定律,我們得到

此方程可以關於 V1 求解

最後,可以透過用數字值替換符號來求解未知電壓。在已知電路中所有電壓後,任何未知電流很容易計算出來。

實際上, ,這意味著電流透過 R1 流動方向相反,這反映了這樣一個事實:假設電流從節點流出只是為了幫助我們編寫能夠捕獲電路拓撲的方程,以便寫出邏輯一致的方程。它們決不是對最終電流方向的猜測。
,這意味著電流透過 R1 流動方向相反,這反映了這樣一個事實:假設電流從節點流出只是為了幫助我們編寫能夠捕獲電路拓撲的方程,以便寫出邏輯一致的方程。它們決不是對最終電流方向的猜測。
給出下面的電路,找出所有節點的電壓。
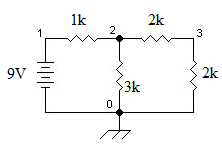 節點分析示例的電路示例。
節點分析示例的電路示例。
- 節點 0:
 (定義為接地節點)
(定義為接地節點)
- 節點 1:
 (自由節點電壓)
(自由節點電壓)
- 節點 2:

- 節點 3:

從而得出以下線性方程組

因此,解為

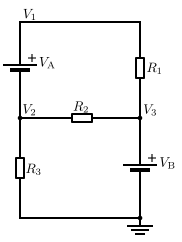 在這個電路中,VA 在兩個未知電壓之間,因此是一個超級節點。
在這個電路中,VA 在兩個未知電壓之間,因此是一個超級節點。
在這個電路中,我們最初有兩個未知電壓,V1 和 V2。由於電壓源的另一端位於接地電位,因此 V3 上的電壓已知為 VB。
流過電壓源 VA 的電流無法直接計算。因此,我們無法編寫 V1 或 V2 的電流方程。但是,我們知道離開節點 V2 的電流必須進入節點 V1。儘管節點無法單獨求解,但我們知道這兩個節點的組合電流為零。這種將兩個節點組合在一起稱為超級節點技術,它需要一個額外的方程:V1 = V2 + VA。
該電路的完整方程組為

將 V1 代入第一個方程,並針對 V2 求解,我們得到






















