電路理論/RLC 電路
外觀
< 電路理論
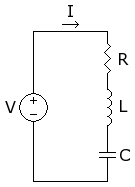
其特徵方程為
其中
當
- 該方程只有一個實根。
- I 對 t 的解為
- I-t 曲線看起來像
當
- 該方程有兩個實根。
- 對於
- I-t 曲線看起來像
當
- 該方程有兩個復根。
- 對於
- I-t 曲線看起來像
阻尼係數是指電路振盪隨時間逐漸衰減的程度。我們定義阻尼比為
| 電路型別 | 串聯 RLC | 並聯 RLC |
|---|---|---|
| 阻尼係數 | ||
| 諧振頻率 |
比較阻尼係數和諧振頻率可以得出不同型別的電路:過阻尼、欠阻尼和臨界阻尼。
[頻寬]
對於串聯 RLC 電路
對於並聯 RLC 電路
[品質因數]
對於串聯 RLC 電路
對於並聯 RLC 電路
由於電感器和電容器對不同的輸入有不同的反應,因此當電路受到某些型別和幅度的輸入時,其響應有可能趨於無窮大。當電路的輸出趨於無窮大時,該電路被稱為不穩定。不穩定的電路實際上可能很危險,因為不穩定的元件會過熱並可能破裂。
當“行為良好”的輸入產生“行為良好”的輸出響應時,電路被認為是穩定的。“行為良好”一詞在不同的應用中含義不同,但通常是指有限且可控的數量。
當 R = 0 時,電路簡化為一個串聯 LC 電路。當電路處於共振狀態時,電路將在共振頻率下振動。
電路會振動,並且可能會產生駐波,具體取決於驅動訊號的頻率、振盪波的波長以及電路的幾何形狀。
當 R ≠ 0 且電路工作在共振狀態時。
- 頻率相關的元件 L 和 C 會相互抵消,即 ZL - ZC = 0,因此電路的總阻抗為
- 電路的電流為
- 工作頻率為
如果將電阻值增加一倍,電流減半,則
- 電路在 頻率範圍內保持穩定。
該電路能夠選擇頻寬,使其在該頻寬內保持穩定。因此,它最適合用作調諧諧振選擇頻寬濾波器。
使用 L 或 C 將電路調諧到共振頻率 。電流達到最大值 。降低電流,高於 ,電路將對比 更窄的頻寬做出響應。降低電流,低於 ,電路將對比 更寬的頻寬做出響應。
結論
[edit | edit source]| 電路 | 通用 | 串聯 RLC | 並聯 RLC |
|---|---|---|---|
| 電路 |  |
 | |
| 阻抗 | Z | ||
| 根 | λ | λ = | λ = |
| I(t) | Aeλ1t + Beλ2t | Aeλ1t + Beλ2t | Aeλ1t + Beλ2t |
| 阻尼係數 | |||
| 諧振頻率 | |||
| 頻寬 | |||
| 品質因數 |













![{\displaystyle I(t)=e^{\left(-\alpha +{\sqrt {\alpha ^{2}-\beta ^{2}}}\right)t}+e^{\left(-\alpha -{\sqrt {\alpha ^{2}-\beta ^{2}}}\right)t}=e^{-\alpha }\left[e^{\sqrt {\alpha ^{2}-\beta ^{2}}}+e^{-{\sqrt {\alpha ^{2}-\beta ^{2}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f57838d46132e8865722793d4fdcfa88a25427d)



![{\displaystyle I(t)=e^{\left(-\alpha +{\sqrt {\beta ^{2}-\alpha ^{2}}}t\right)}+e^{\left(-\alpha -{\sqrt {\beta ^{2}-\alpha ^{2}}}t\right)}=e^{-\alpha }\left[e^{j\left({\sqrt {\beta ^{2}-\alpha ^{2}}}t\right)}+e^{-j\left({\sqrt {\beta ^{2}-\alpha ^{2}}}t\right)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40ff5495f4643e6796703fe2c08f7bc0ce6ba357)













![{\displaystyle Z_{R}+Z_{L}+Z_{C}=R+[Z_{L}-Z_{C}]=R+0=R}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6178efb58a3bb6868624d88437ba9dd10bd92c00)













