電路理論/二階解

== 二階解

本頁將討論二階 RLC 電路的解。二階解相當複雜，要完全理解它需要了解微分方程。本書不需要你瞭解微分方程，因此我們將描述解，而不會展示如何推導它們。推導可能會被放在另一章中，最終。

本章的目的是推導二階電路的完全響應。確定完全響應涉及許多步驟

1. 獲得電路的微分方程
2. 確定諧振頻率和阻尼比
3. 獲得電路的特徵方程
4. 求解特徵方程的根
5. 求解自然響應
6. 求解強迫響應
7. 求解完全響應

我們將逐一討論所有這些步驟。

求解微分方程

二階電路只有在獲得描述電路的二階微分方程後才能求解。我們將在這裡討論一些用於獲得 RLC 電路二階微分方程的技術。

注意

並聯 RLC 電路使用電壓的常微分方程更容易求解（基爾霍夫電壓定律的結果），串聯 RLC 電路使用電流的常微分方程更容易求解（基爾霍夫電流定律的結果）。

直接法

求解電路微分方程最直接的方法是對電路進行節點分析或網孔電流分析，然後求解輸入函式的方程。最終方程應該只包含導數，不包含積分。

變數法

如果我們建立兩個變數 g 和 h，我們可以用它們建立一個二階微分方程。首先，我們將 g 和 h 設定為電感電流、電容電壓或兩者。接下來，我們建立一個只有一個一階微分方程，它有 g = f(g, h)。然後，我們寫另一個一階微分方程，其形式為

${\frac {dh}{dt}}=Kg$ 或 ${\frac {1}{K}}{\frac {dh}{dt}}=g$

接下來，我們將第二個方程代入第一個方程，我們就得到一個二階方程。

零輸入響應

電路的零輸入響應是指當沒有激勵函式（沒有電流輸入，也沒有電壓輸入）時電路的狀態。我們可以將微分方程設定為

${{d^{2}i} \over {dt^{2}}}+2\zeta {{di} \over {dt}}+\omega _{o}^{2}i(t)=0$

這導致了電路的特徵方程，將在下面解釋。

特徵方程

RLC 電路的特徵方程使用下面描述的“運算元法”獲得，其中輸入為零。RLC 電路（串聯或並聯）的特徵方程將是

$s^{2}i+{R \over L}si+{1 \over {LC}}i=0$

特徵方程的根是我們正在尋找的“解”。

求解特徵方程

這種獲得特徵方程的方法需要一點技巧。首先，我們建立一個運算元 s，使得

$sx={\frac {dx}{dt}}$

此外，我們可以將高階運算元表示為

$s^{2}x={\frac {d^{2}x}{dt^{2}}}$

其中 x 是電路源的電壓（在串聯電路中）或電流（在並聯電路中）。我們為電路中的電感電流和/或電容電壓編寫 2 個一階微分方程。我們將所有微分轉換為 s，並將所有積分（如果有）轉換為 (1/s)。然後我們可以使用克萊姆法則求解。

解

特徵方程的解用諧振頻率和阻尼比表示

[特徵方程解]

$s=-\zeta \pm {\sqrt {\zeta ^{2}-\omega _{o}^{2}}}$

如果這兩個值中的任何一個都用於假設解中的s $x=Ae^{st}$並且該解完成了微分方程，那麼它可以被認為是一個有效的解。我們將在下面進一步討論這一點。

阻尼

電路的解取決於電路表現出的阻尼型別，這由阻尼比與諧振頻率之間的關係決定。不同的阻尼型別包括過阻尼、欠阻尼和臨界阻尼。

過阻尼

RLC 串聯過阻尼響應

當滿足以下條件時，電路稱為過阻尼

$\zeta >\omega _{0}$

在這種情況下，特徵方程的解是兩個不同的正數，由以下公式給出

$I(t)=Ae^{\ s_{1}t}+Be^{\ s_{2}t}$，其中

$s_{1},s_{2}=-\zeta \pm {\sqrt {\zeta ^{2}-\omega _{0}^{2}}}$

在並聯電路中

$\zeta =1/(2RC)$

$\omega _{0}=1/{\sqrt {(LC)}}$

在串聯電路中

$\zeta =R/(2L)$

$\omega _{0}=1/{\sqrt {(LC)}}$

過阻尼電路的特點是穩定時間很長，並且可能存在較大的穩態誤差。

欠阻尼

當阻尼比小於諧振頻率時，電路稱為欠阻尼。

$\zeta <\omega _{0}$

在這種情況下，特徵多項式的解是共軛複數。這會導致電路中出現振盪或振鈴。該解包含兩個共軛根

$\lambda _{1}=-\zeta +i\omega _{c}$

和

$\lambda _{2}=-\zeta -i\omega _{c}$

其中

$\omega _{c}={\sqrt {-(\omega _{o}^{2}-\zeta ^{2})}}$

該解決方案是

$i(t)=Ae^{(-\zeta +i\omega _{c})t}+Be^{(-\zeta -i\omega _{c})t}$

其中 A 和 B 是任意常數。使用尤拉公式，我們可以將解簡化為

$i(t)=e^{-\zeta t}\left[C\sin(\omega _{c}t)+D\cos(\omega _{c}t)\right]$

其中 C 和 D 是任意常數。這些解的特點是 指數衰減的正弦響應。品質因數（見下文）越高，振盪衰減所需的時間就越長。

臨界阻尼

RLC 串聯臨界阻尼

如果阻尼係數或實際阻尼與臨界阻尼之比等於 1，則電路稱為 臨界阻尼

$\zeta =1$

在這種情況下，特徵方程的解是二重根。兩個根是相同的（$\lambda _{1}=\lambda _{2}=\lambda$），解為

$I(t)=(A+Bt)e^{\lambda t}$

其中 A 和 B 是任意常數。臨界阻尼電路通常具有較低的過沖、沒有振盪和較快的穩定時間。

串聯 RLC

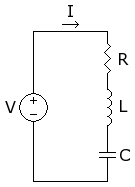一個串聯 RLC 電路。

具有恆定電壓源 V 和電阻 R、電容 C 和電感 L 的簡單串聯電路的微分方程為

$L{\frac {d^{2}q}{dt^{2}}}+R{\frac {dq}{dt}}+{1 \over C}q=0$

因此，特徵方程如下

$Ls^{2}+Rs+{1 \over C}=0$

有兩個根

$s_{1}=-{R \over 2L}+{\sqrt {({R \over 2L})^{2}-{1 \over LC}}}$

和

$s_{2}=-{R \over 2L}-{\sqrt {({R \over 2L})^{2}-{1 \over LC}}}$

並聯 RLC

一個並聯 RLC 電路。

具有電阻 R、電容 C 和電感 L 的並聯 RLC 電路的微分方程如下

$C{\frac {d^{2}v}{dt^{2}}}+{\frac {1}{R}}{\frac {dv}{dt}}+{1 \over L}v=0$

其中 v 是電路上的電壓。因此，特徵方程如下

$Cs^{2}+{1 \over R}s+{1 \over L}=0$

有兩個根

$s_{1}=-{1 \over 2RC}+{\sqrt {({1 \over 2RC})^{2}-{1 \over LC}}}$

和

$s_{2}=-{1 \over 2RC}-{\sqrt {({1 \over 2RC})^{2}-{1 \over LC}}}$

電路響應

一旦我們得到了微分方程和特徵方程，我們就可以組裝電路響應的數學形式。RLC電路的微分方程形式為

$a_{2}{\frac {d^{2}x}{dt^{2}}}+a_{1}{\frac {dx}{dt}}+a_{0}x=f(t)$

其中f(t)是RLC電路的激勵函式。

自然響應

電路的自然響應是指給定電路對零輸入的響應（即僅取決於初始條件值）。電路的自然響應將記為x_n(t)。系統的自然響應必須滿足電路的無激勵微分方程

[無激勵函式]

$a_{2}{\frac {d^{2}x}{dt^{2}}}+a_{1}{\frac {dx}{dt}}+a_{0}x=0$

我們記得這個方程是上面討論的“零輸入響應”。現在我們定義自然響應為指數函式

$x_{n}=A_{1}e^{st}+A_{2}e^{st}$

其中s是電路特徵方程的根。選擇x_n的這個特定解的原因是基於微分方程理論，我們將暫時不加證明地接受它。我們可以使用兩個方程組來求解常數值

$x(0)=A_{1}+A_{2}$

${\frac {dx(0)}{dt}}=s_{1}A_{1}+s_{2}A_{2}$

其中x是電壓（在並聯電路中的元件）或電流（在串聯電路中的元件）。

強迫響應

電路的強迫響應是指電路對輸入激勵函式的響應方式。強迫響應記為x_f(t)。

其中強迫響應必須滿足強迫微分方程

[強迫函式]

$a_{2}{\frac {d^{2}x}{dt^{2}}}+a_{1}{\frac {dx}{dt}}+a_{0}x=f(t)$

強迫響應是基於輸入函式的，因此我們無法給出它的通用解。但是，我們可以針對不同的輸入提供一組解

輸入形式	輸出形式
K（常數）	A（常數）
$M\sin(\omega t)$	$A\sin(\omega t)+B\cos(\omega t)$
$Me^{-at}$	$Ae^{-at}$

完整響應

電路的完整響應是系統強迫響應和自然響應的總和。

[完整響應]

$x_{c}(t)=x_{t}(t)+x_{s}(t)$

一旦我們推匯出電路的完整響應，我們就可以說我們已經“解決了”電路，並完成了工作。

當電路中沒有 R 時，二階電路 (LC) 被認為 a=1/2RC（如果電路並聯）= 0，所以由於 a=0 且 omega 的值大於零，電路將處於欠阻尼狀態。