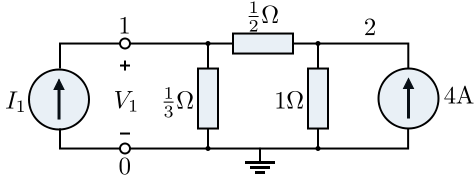電路理論/二埠網路

放大器是現存最有用的電路之一。它們幾乎存在於每個電子裝置中，從收音機和電視到洗衣機和示波器。它們構成了幾乎所有更復雜電路的基礎。放大器是一種接收輸入並輸出與其成比例（但不一定更大）的裝置。我們可以將此表示為一個二埠電路，它具有一個輸入埠和一個輸出埠。

首先，讓我們考慮我們已經熟悉的一埠電路

基本電路元件，如電阻器、電容器、電感器和獨立電源，構成了最基本的一埠電路。更一般地，一個一埠電路可以包含任意數量的無源元件、獨立和受控電源以及節點。通常，一旦設計了這些電路之一，我們就不再關心它是如何工作的，並很樂意用它在埠處的行為來表示它。透過使用我們已經學習的技術，我們可以將其簡化為一個戴維寧或諾頓等效電路。

現在，考慮下面的二埠電路

某些器件具有超過兩個端子，例如具有三個端子的 BJT 和具有三個或四個端子的 MOSFET。在這些情況下，無法將其表示為一埠電路，二埠電路是唯一的選擇。二埠電路與一埠電路具有相同的應用，即它們允許我們只考慮電路的行為，而不是不必要的內部細節。

一埠電路回顧

在本節中，我們將再次研究一埠電路，並考慮一種更系統的方法來尋找諾頓和戴維寧等效電路。

示例 1

考慮以下電路

讓我們計算由節點 $a$ 和 $b$ 構成的埠看進去的戴維寧和諾頓等效電路。為了找到開路電壓，我們使用電流分配規則找到流過 1/3 Ω 電阻器的電流，並乘以 1/3

$v_{oc}={\frac {1}{{\frac {1}{2}}+{\frac {1}{3}}+1}}\times 4\times {\frac {1}{3}}={\frac {8}{11}}{\mbox{ V}}$

透過停用電流源並找到相應的阻抗來找到等效電阻

$R_{eq}={\frac {{\frac {1}{3}}\times \left({\frac {1}{2}}+1\right)}{{\frac {1}{3}}+\left({\frac {1}{2}}+1\right)}}={\frac {3}{11}}\,\Omega$

短路電流可以按如下方式找到

$i_{sc}={\frac {v_{oc}}{R_{eq}}}={\frac {8}{3}}{\mbox{ A}}$

因此，我們有以下戴維寧和諾頓等效電路

戴維寧和諾頓電路是原始電路的簡化：無論原始電路有多少個節點，等效電路只有兩個（這裡，0 和 1）。我們可以將此過程視為消除非埠端子節點（在本例中為節點 2）的過程。我們可以使用節點分析的系統方法來實現這一點。

為此，我們將節點 0 定義為參考節點，並在節點 0 和 1 之間放置一個測試電流源

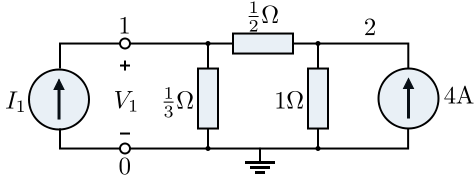
我們現在可以執行逐個檢查的節點分析

${\begin{bmatrix}5&-2\\-2&3\end{bmatrix}}{\begin{bmatrix}V_{1}\\V_{2}\end{bmatrix}}={\begin{bmatrix}I_{1}\\4\end{bmatrix}}$

節點 2 不是埠節點，因此必須將其消除。我們可以使用高斯消元法來實現這一點。關於“3”進行主元操作

${\begin{bmatrix}5&-2\\-2&\mathbf {3} \end{bmatrix}}{\begin{bmatrix}V_{1}\\V_{2}\end{bmatrix}}={\begin{bmatrix}I_{1}\\4\end{bmatrix}}$

${\begin{bmatrix}5-{\frac {(-2)(-2)}{3}}\end{bmatrix}}{\begin{bmatrix}V_{1}\end{bmatrix}}={\begin{bmatrix}I_{1}-{\frac {(-2)4}{3}}\end{bmatrix}}$

${\begin{bmatrix}{\frac {11}{3}}\end{bmatrix}}{\begin{bmatrix}V_{1}\end{bmatrix}}={\begin{bmatrix}I_{1}+{\frac {8}{3}}\end{bmatrix}}$

此結果方程可以用電流或電壓形式表示。

$I_{1}={\frac {11}{3}}V_{1}-{\frac {8}{3}}\quad {\mbox{or}}\quad V_{1}={\frac {3}{11}}I_{1}+{\frac {8}{11}}$

很明顯，這些對應於我們之前找到的戴維南和諾頓等效電路。如果電路沒有獨立電源，我們只會得到一個對應於單個電阻的表示式。

示例 2

現在讓我們考慮以下稍微複雜一點的例子。