通訊系統/噪聲係數

此頁面將討論噪聲對傳輸系統的影響。

噪聲型別

大多數人為的電磁噪聲出現在 500 MHz 以下的頻率。其中最重要的是

• 水力線

• 點火系統

• 熒光燈

• 電機

因此，深空網路被放置在沙漠中，遠離這些干擾源。

還有一些自然噪聲源，不容易避免，例如

•大氣噪聲 - 閃電 < 20 MHz

•太陽噪聲 - 太陽 - 11 年太陽黑子週期

•宇宙噪聲 - 8 MHz 到 1.5 GHz

•熱噪聲或約翰遜噪聲。由於自由電子撞擊振動離子而產生。

•白噪聲 - 白噪聲在指定頻率範圍內具有恆定的頻譜密度。約翰遜噪聲是白噪聲的一個例子。

•高斯噪聲 - 高斯噪聲本質上是完全隨機的，但是，任何特定幅度值的機率都遵循正態分佈曲線。約翰遜噪聲本質上是高斯噪聲。

•散粒噪聲 - 雙極型電晶體

$i_{n}={\sqrt {2qI_{dc}\Delta f}}$

其中 q = 電子電荷 1.6 x 10^-19 庫侖

•過剩噪聲、閃爍噪聲、1/f 噪聲和粉紅噪聲 < 1 KHz 與頻率成反比，與溫度和直流電流成正比

•傳輸時間噪聲 - 發生在電子穿過結的傳輸時間與訊號週期相同時。

在這些噪聲中，只有約翰遜噪聲可以很容易地分析和補償。噪聲功率由下式給出

$P_{n}=kTB$

其中

k = 玻爾茲曼常數 (1.38 x 10^-23 J/K)

T = 開爾文溫度

B = 頻寬，單位為 Hz

此方程適用於銅線繞制電阻器，但對於所有電阻器都足夠接近。當源阻抗和負載阻抗相等時，會發生最大功率傳輸。

噪聲電壓的組合

兩個噪聲電壓的瞬時值只是它們在同一時刻的個體值的總和。

$v_{total\;inst}=v_{1\;inst}+v_{2\;inst}$

此結果在示波器上很容易觀察到。但是，它沒有特別有用，因為它不會產生像電壓表測量的單個穩定的數值。

如果兩個電壓是相干的 [K = 1]，則總的有效值等於各個有效值的總和。

$v_{total\;rms}=v_{1\;rms}+v_{2\;rms}$

如果兩個訊號彼此完全隨機 [K = 0]，例如約翰遜噪聲源，則總功率等於所有各個功率的總和

$P_{total\;random\;noise}=P_{n1\;random}+P_{n2\;random}$

功率為 P = kTB 的約翰遜噪聲可以被認為是透過電阻器施加的噪聲電壓，即戴維南等效。

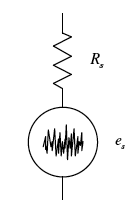
這種噪聲源的例子可能是電纜或傳輸線。從源傳遞到負載（例如放大器輸入）的噪聲功率量是源阻抗和負載阻抗的函式。

如果負載阻抗為 0 $\Omega$，則不會向其傳輸任何功率，因為電壓為零。如果負載具有無限的輸入阻抗，同樣也不會向其傳輸任何功率，因為沒有電流。當源阻抗和負載阻抗相等時，會發生最大功率傳輸。

$P_{L\;\max }={\frac {e_{s}^{2}}{4R_{s}}}$

在最大功率傳輸時，有效噪聲電壓為

$e_{n}={\sqrt {4RP}}={\sqrt {4RkTB}}$

觀察如果噪聲電阻分解成兩個分量會發生什麼

$e_{n}^{2}=4RkTB=4\left({R_{1}+R_{2}}\right)kTB=e_{n1}^{2}+e_{n2}^{2}$

由此可見，隨機噪聲電阻可以直接相加，但隨機噪聲電壓則以向量方式相加

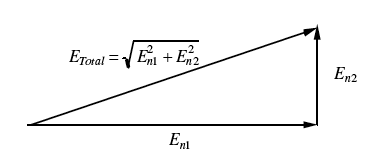
如果噪聲源不是完全隨機，它們之間存在某種相關性 [0 < K < 1]，則組合結果就不那麼容易計算了

$P_{Total\;\left({{\rm {not}}\;{\rm {quite}}\;{\rm {random}}}\right)}={\frac {E_{1}^{2}+E_{2}^{2}+2KE_{1}E_{2}}{R_{0}}}=P_{1}+P_{2}=2K{\sqrt {P_{1}+P_{2}}}$

其中

K = 相關性 [0 < K < 1]

R₀ = 參考阻抗

噪聲溫度

給定傳輸介質中的噪聲量可以等效為熱噪聲。熱噪聲經過充分研究，因此在可能的情況下重複使用相同的方程很有意義。為此，我們可以說，任何數量的輻射噪聲都可以用給定有效溫度的熱噪聲來近似。有效溫度以開爾文為單位。有效溫度通常與標準溫度$T_{o}$，即 290 開爾文進行比較。

在微波應用中，很難用電流和電壓來描述訊號，因為訊號更適合用場方程來描述。因此，溫度被用來表徵噪聲。總噪聲溫度等於所有單個噪聲溫度的總和。

噪聲係數

用來量化噪聲的術語可能有點令人困惑，但關鍵定義是

信噪比：它要麼是無量綱的，要麼以 dB 為單位。信噪比可以在系統中的任何地方指定。

${\frac {S}{N}}={\frac {{\rm {signal}}\;{\rm {power}}}{{\rm {noise}}\;{\rm {power}}}}={\frac {P_{s}}{P_{n}}}$

$\left({\frac {S}{N}}\right)_{dB}=10\log {\frac {P_{s}}{P_{n}}}$

噪聲係數（或噪聲比）：$F={\frac {\left({\frac {S}{N}}\right)_{in}}{\left({\frac {S}{N}}\right)_{out}}}$（無量綱）

噪聲係數：$NF=10\log F=SNR_{in}-SNR_{out}$ dB

此引數在所有高效能放大器中都有指定，它衡量放大器本身對總噪聲的貢獻程度。在理想放大器或系統中，NF = 0 dB。本討論未考慮任何降噪技術，如濾波或動態強調。

Friiss 公式及放大器級聯

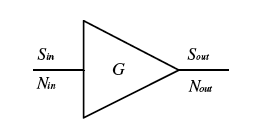
檢查放大器級聯以瞭解噪聲如何在大型通訊系統中累積很有意思。

$F={\frac {\left({\frac {S}{N}}\right)_{in}}{\left({\frac {S}{N}}\right)_{out}}}={\frac {S_{in}}{N_{in}}}\times {\frac {N_{out}}{S_{out}}}$

放大器增益可以定義為：$G={\frac {S_{out}}{S_{in}}}$

因此，輸出訊號功率為：$S_{out}=GS_{in}$

噪聲係數（比）可以改寫為：$F={\frac {S_{in}}{N_{in}}}\times {\frac {N_{out}}{GS_{in}}}={\frac {N_{out}}{GN_{in}}}$

輸出噪聲功率現在可以寫成：$N_{out}=FGN_{in}$

從這裡我們可以觀察到，輸入噪聲在透過放大器時，會隨著噪聲係數和放大器增益而增加。一個無噪聲放大器將具有1的噪聲係數（因子）或0 dB的噪聲係數。在這種情況下，輸入噪聲只會因增益而放大，因為放大器不會產生噪聲。

任何系統都可以接收的最小噪聲是約翰遜噪聲。

$N_{in\left({\rm {minimum}}\right)}=kTB$

因此，任何放大器的輸出端可以出現的最小噪聲為

$N_{out\left({\rm {minimum}}\right)}=FGkTB$

一個理想放大器的輸出噪聲將是（F = 1）

$N_{out\left({\rm {perfect}}\right)}=GkTB$

這兩個值之間的差異是放大器本身產生的（新增的）噪聲。

$N_{out\left({\rm {added}}\right)}=N_{out\left({\rm {minimum}}\right)}-N_{out\left({\rm {perfect}}\right)}=FGkTB-GkTB=\left({F-1}\right)GkTB$

這是出現在輸出端的附加（產生的）噪聲。

放大器的總輸出噪聲由下式給出

$N_{total}=N_{out\left({\rm {perfect}}\right)}+N_{out\left({\rm {added}}\right)}=GkTB+\left({F-1}\right)GkTB$

如果再串聯一個放大器，總的輸出噪聲將包含第一級噪聲經第二級增益放大後的結果，再加上第二級放大器的附加噪聲。

$N_{total}=G_{1}G_{2}kTB+\left({F_{1}-1}\right)G_{1}G_{2}kTB+\left({F_{2}-1}\right)G_{2}kTB$

如果我們將這個表示式的兩邊除以公因子：$G_{1}G_{2}kTB$

得到

${\frac {N_{total}}{G_{1}G_{2}kTB}}={\frac {G_{1}G_{2}kTB+\left({F_{1}-1}\right)G_{1}G_{2}kTB+\left({F_{2}-1}\right)G_{2}kTB}{G_{1}G_{2}kTB}}$

回顧：$F={\frac {N_{out}}{GN_{in}}}={\frac {N_{total}}{G_{1}G_{2}kTB}}$

因此：$F_{overall}=F_{1}+{\frac {F_{2}-1}{G_{1}}}$

這個過程可以擴充套件到包含更多級聯放大器，從而得出

Friiss 公式

$F=F_{1}+{\frac {F_{2}-1}{G_{1}}}+{\frac {F_{3}-1}{G_{1}G_{2}}}+$

這個公式表明，級聯絡統的整體噪聲係數在很大程度上由第一級放大器的噪聲係數決定，因為任何級的噪聲貢獻都被前面級的增益所劃分。這就是為什麼任何通訊系統中的第一級應該是 LNA (低噪聲放大器) 的原因。

接收機靈敏度

在給定的頻寬 W 中，我們可以證明噪聲功率 N 等於

$N=F(kT_{0})W$

從 N，我們可以證明接收機靈敏度等於

$SNR\times N$