通訊系統/有線傳輸

本頁將討論訊號透過物理介質（如電線）傳播的主題。

傳輸線方程

許多型別的通訊系統都需要訊號在某個點透過銅線傳遞。

以下分析需要兩個假設

• 傳輸線可以分解成小的、分散式的無源電氣元件

• 這些元件與頻率無關（即雖然電抗是頻率的函式，但電阻、電容和電感不是）

這兩個假設將以下分析限制在低 MHz 區域的頻率。第二個假設特別難以辯護，因為眾所周知，導線的電阻會隨著頻率的增加而增加，因為導電截面積會減小。這種現象被稱為趨膚效應，很難評估。

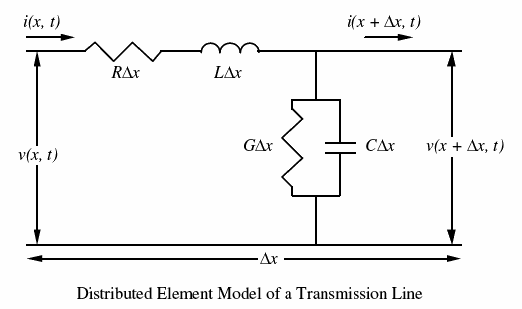
以下數學操作背後的目的是獲得一個表示式，該表示式定義了在任何時間（t）沿傳輸線的任何部分（x）的電壓（或電流）。稍後，這種分析將擴充套件到包括頻域。

回想一下電感器和電容器的特徵方程

$v=L{\frac {\partial i}{\partial t}}$ 和 $i=C{\frac {\partial v}{\partial t}}$

基爾霍夫電壓定律

基爾霍夫電壓定律 (KVL) 簡而言之，就是在一個閉合迴路中，所有電壓勢的總和等於零。或者換句話說，如果你走上山坡，然後走下山坡，淨海拔變化將為零。

在上面的電路中應用 KVL，我們得到

$v\left({x,t}\right)=R\Delta xi\left({x,t}\right)+L\Delta x{\frac {\partial i}{\partial t}}\left({x,t}\right)+v\left({x+\Delta x,t}\right)$

重新排列

$v\left({x,t}\right)-v\left({x+\Delta x,t}\right)=R\Delta xi\left({x,t}\right)+L\Delta x{\frac {\partial i}{\partial t}}\left({x,t}\right)$

但上述方程的 LHS（左側），表示電纜元件 $\Delta v$ 上的電壓降，因此

$\Delta v=R\Delta xi\left({x,t}\right)+L\Delta x{\frac {\partial i}{\partial t}}\left({x,t}\right)$

除以 $\Delta x$，我們得到

${\frac {\Delta v}{\Delta x}}=Ri\left({x,t}\right)+L{\frac {\partial i}{\partial t}}\left({x,t}\right)$

LHS 很容易被識別為導數。簡化符號

${\frac {\partial v}{\partial x}}=Ri+L{\frac {\partial i}{\partial t}}$

此表示式包含電流和電壓。將方程寫成電流或電壓作為距離或時間的函式會很方便。

簡化方程（相信我）

分離電壓和電流的第一步是對位置x求導（**方程式 1**）

${\frac {\partial ^{2}v}{\partial x^{2}}}=R{\frac {\partial i}{\partial x}}+L{\frac {\partial ^{2}i}{\partial x\partial t}}$

下一步是消除電流項，只留下包含電壓的表示式。電流沿線的變化等於透過電容C和電導G並聯到線的電流。透過在電路中應用 KCL，我們可以獲得必要的資訊（**方程式 2**）

${\frac {\partial i}{\partial x}}=Gv+C{\frac {\partial v}{\partial t}}$

對時間求導，我們得到（**方程式 3**）

${\frac {\partial ^{2}i}{\partial x\partial t}}=G{\frac {\partial v}{\partial t}}+C{\frac {\partial ^{2}v}{\partial t^{2}}}$

將（**方程式 2**）和（**方程式 3**）代入（**方程式 1**），我們得到所需的簡化

${\frac {\partial ^{2}v}{\partial x^{2}}}=R\left[{Gv+C{\frac {\partial v}{\partial t}}}\right]+L\left[{G{\frac {\partial v}{\partial t}}+C{\frac {\partial ^{2}v}{\partial t^{2}}}}\right]$

收集這些項，我們得到

電壓的傳輸線方程

${\frac {\partial ^{2}v}{\partial x^{2}}}=RGv+\left({RC+LG}\right){\frac {\partial v}{\partial t}}+LC{\frac {\partial ^{2}v}{\partial t^{2}}}$

該方程被稱為傳輸線方程。注意，它具有任何特定位置x處的電壓作為時間t的函式。

類似地，對於電流，我們得到

電流的傳輸線方程

${\frac {\partial ^{2}i}{\partial x^{2}}}=RGi+\left({RC+LG}\right){\frac {\partial i}{\partial t}}+LC{\frac {\partial ^{2}i}{\partial t^{2}}}$

但我們還沒有完全完成。

求解傳輸線方程

從歷史上看，數學家會透過假設v的解，將其代入方程，並觀察結果是否有意義來求解傳輸線方程中的v。工程師會透過基於一些實驗室實驗的“有根據的猜測”來遵循類似的程式，關於解可能是什麼。如今，有更復雜的技術用於尋找解決方案。在這方面，工程師在尋找數學工具的應用方面可能比數學家落後幾個世紀。

為了求解傳輸線方程，我們將猜測電壓函式的解的形式為

$v\left(t\right)=e^{j\omega t}e^{-\gamma x}$

第一項表示一個以角速度 $\omega$ 弧度每秒旋轉的單位向量，換句話說，是某個頻率的正弦波。第二項表示正弦波被傳輸線修改，即其幅度隨距離呈指數衰減。如果我們讓 $\gamma$ 是一個複數，我們也可以包括訊號沿線路傳播時發生的任何相位變化。

正弦波用作訊號源是因為它易於生成並進行數學操作。尤拉恆等式顯示了指數表示法和三角函式之間的關係

尤拉恆等式

$e^{j\omega t}=\cos \left({\omega t}\right)+j\sin \left({\omega t}\right)$

回到我們的猜測，我們設 $\gamma =\alpha +j\beta$，因此

$v\left(t\right)=e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}=e^{-\alpha x}e^{\left({\omega t-\beta x}\right)j}$

項 $e^{-\alpha x}$ 表示訊號沿線路傳播時的指數幅度衰減。 $\alpha$ 稱為衰減係數，以每米尼泊爾表示。

項 $e^{\left({\omega t-\beta x}\right)j}$ 表示線路任意點上的訊號頻率。 $\beta$ 分量稱為相移係數，以弧度每米表示。

將我們的猜測

$v\left(t\right)=e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$

代入電壓的傳輸線方程，我們得到

${\frac {\partial ^{2}}{\partial x^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=RG\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]+\left({RC+LG}\right){\frac {\partial }{\partial t}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]+LC{\frac {\partial ^{2}}{\partial t^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]$

這個公式看起來很嚇人，但如果你能進行基本微分和代數運算，你就能解決它！

簡化方程式（相信我）

現在我們的目標是逐步進行數學運算，看看能否得到一個合理的解。如果我們得出矛盾的結果或不合理的結論，那就意味著我們的推測是錯誤的，我們需要進行更多的實驗，並提出更好的猜測來解釋電壓和電流在傳輸線上的傳播方式。

讓我們逐項分析這個公式

LHS = RHS Term 1 + RHS Term 2 + RHS Term 3

從左側 (LHS) 開始，我們得到以下簡化結果

${\frac {\partial ^{2}}{\partial x^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]={\frac {\partial }{\partial x}}\left[{-\left({\alpha +j\beta }\right)e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=\left({\alpha +j\beta }\right)^{2}e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$

信不信由你，RHS Term 1 不需要簡化。

簡化 RHS Term 2，我們得到

$\left({RC+LG}\right){\frac {\partial }{\partial t}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=\left({RC+LG}\right)j\omega \left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)$

簡化 RHS Term 3，我們得到

$LC{\frac {\partial ^{2}}{\partial t^{2}}}\left[{e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=LC{\frac {\partial }{\partial t}}\left[{j\omega e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right]=-LC\omega ^{2}e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$

讓我們把所有東西重新組合在一起

$\left({\alpha +j\beta }\right)^{2}e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}=RG\left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)+\left({RC+LG}\right)j\omega \left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)-LC\omega ^{2}\left({e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}}\right)$

請注意，這四個項中的每一個都包含表示式 $e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}$。

因此，我們最終得到

$\left({\alpha +j\beta }\right)^{2}=RG+\left({RC+LG}\right)j\omega -LC\omega ^{2}$

這可以進一步簡化為

衰減和相移係數

$\alpha +j\beta =\gamma ={\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}$

這個結果不矛盾也不不合理。因此，我們得出結論，我們的推測是正確的，我們已經成功地找到了傳輸線上的衰減和相移的表示式，該表示式是其分散式電氣元件和頻率的函式。

無損傳輸線

訊號損耗透過兩種基本機制發生：訊號功率可以在電阻器 [或電導] 中消散，或者訊號電流可以透過電抗並聯到交流地。在傳輸線理論中，無損傳輸線不會消散功率。然而，訊號仍然會逐漸衰減，因為並聯電抗透過接地路徑將電流返回到電源。為了使功率損耗等於零，R = G = 0。當傳輸線非常短時，會發生這種情況。示波器探頭是極短傳輸線的示例。傳輸線方程簡化為電壓方程

${\frac {\partial ^{2}v}{\partial x^{2}}}=LC{\frac {\partial ^{2}v}{\partial t^{2}}}$

和電流方程

${\frac {\partial ^{2}i}{\partial x^{2}}}=LC{\frac {\partial ^{2}i}{\partial t^{2}}}$

為了確定正弦訊號如何受到此類線路的影響，我們可以簡單地將正弦電壓或電流代入上述表示式並像以前一樣求解，或者我們可以採用更簡單的方法。我們可以從一般情況的解開始

$\alpha +j\beta =\gamma ={\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}$

令 *R* = *G* = 0，並簡化

$\alpha +j\beta ={\sqrt {\left({j\omega L}\right)\left({j\omega C}\right)}}=\omega \left({LC}\right)^{2}j$

等式實部和虛部

$\alpha =0$

$\beta =\omega {\sqrt {LC}}$

這個表示式告訴我們，**一個在無損傳輸線上傳播的訊號，會經歷一個與其頻率成正比的相移。**

相速度

一個新的引數，稱為相速度，可以從這些變數中提取出來。

$V_{p}={\frac {1}{\sqrt {LC}}}={\frac {\omega }{\beta }}$ 米每秒

相速度是指波前上固定點看起來移動的速度。在導線傳輸線的情況下，它也是傳播速度，通常：0.24c < Vp < 0.9c。

波前上兩個相同點之間的距離是波長 ($\lambda$)，因為一個週期被定義為 2$\pi$ 弧度。

$\lambda ={\frac {2\pi }{\beta }}$ 並且 $\omega =2\pi f$

因此

$V_{p}=\lambda f$

在自由空間中，相速度為 3 x 10⁸ 米/秒，即光速。在電纜中，相速度略低，因為訊號是由電子傳播的。在波導傳輸線中，相速度超過光速。

無失真傳輸線

無失真線不會扭曲訊號相位，但會引入訊號損耗。由於常見的傳輸線不是超導體，訊號幅度會減小，但會保持與輸入相同的形狀。這種特性對於長電纜系統至關重要。

如果相速度 V_p 在所有頻率下保持恆定，則不會發生相位失真。

根據定義，在一個波長 $\lambda$ 上會發生 2$\pi$ 弧度的相移。

由於

$V_{p}=\lambda f\quad \quad \lambda ={\frac {2\pi }{\beta }}\quad \quad f={\frac {\omega }{2\pi }}$

那麼

$V_{p}={\frac {2\pi }{\beta }}\times {\frac {\omega }{2\pi }}={\frac {\omega }{\beta }}$

這告訴我們，為了使相速度 V_p 保持恆定，相移係數 $\beta$ 必須與頻率 $\omega$ 成正比變化。

回顧

$\gamma ={\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}=\alpha +j\beta$

現在的問題是找到$\beta$. 這可以透過以下步驟完成。

$\gamma ={\sqrt {\left({\frac {R+j\omega L}{j\omega L}}\right)\left({j\omega L}\right)\left({\frac {G+j\omega C}{j\omega C}}\right)\left({j\omega C}\right)}}=j\omega {\sqrt {LC}}{\sqrt {1+{\frac {R}{j\omega L}}}}{\sqrt {1+{\frac {G}{j\omega C}}}}$

看起來我們丟失了$\beta$，但不要放棄。第二和第三個根可以使用二項式展開式展開。

回顧

$\left({1+x}\right)^{n}=1+nx+{\frac {n\left({n-1}\right)}{2!}}x^{2}+{\frac {n\left({n-1}\right)\left({n-2}\right)}{3!}}x^{3}+\cdots$

在本例中，n = 1/2。由於後續項的貢獻迅速減小，$\gamma$僅擴充套件到3項。

$\gamma \approx j\omega {\sqrt {LC}}\left({1+{\frac {1}{2}}{\frac {R}{j\omega L}}-{\frac {1}{8}}\left({\frac {R}{j\omega L}}\right)^{2}}\right)\left({1+{\frac {1}{2}}{\frac {G}{j\omega C}}-{\frac {1}{8}}\left({\frac {G}{j\omega C}}\right)^{2}}\right)$

這看起來可能很複雜，但請記住這只是代數，它最終會簡化為簡單的優雅形式。展開各項後，我們得到

$\gamma \approx j\omega {\sqrt {LC}}\left\{{\begin{array}{l}1+{\frac {1}{2}}{\frac {G}{j\omega C}}-{\frac {1}{8}}\left({\frac {G}{j\omega C}}\right)^{2}+{\frac {1}{2}}{\frac {R}{j\omega L}}-{\frac {1}{4}}{\frac {RG}{\omega ^{2}LC}}\\-{\frac {1}{16}}{\frac {R}{j\omega L}}\left({\frac {G}{j\omega C}}\right)^{2}-{\frac {1}{8}}\left({\frac {R}{j\omega L}}\right)^{2}\\-{\frac {1}{16}}\left({\frac {R}{j\omega L}}\right)^{2}{\frac {G}{j\omega C}}+{\frac {1}{64}}\left({\frac {R}{j\omega L}}\right)^{2}\left({\frac {G}{j\omega C}}\right)^{2}\\\end{array}}\right\}$

由於 $\gamma =\alpha +j\beta$，我們只需要將實部和虛部等式求解即可得到 $\beta$。

$\beta \approx \omega {\sqrt {LC}}\left\{{1+\underbrace {{\frac {1}{8}}\left({\frac {G}{\omega C}}\right)^{2}-{\frac {1}{4}}{\frac {RG}{\omega ^{2}LC}}+{\frac {1}{8}}\left({\frac {R}{\omega L}}\right)^{2}} _{{\rm {Difference}}\;{\rm {of}}\;{\rm {squares}}}+\underbrace {{\frac {1}{64}}\left({\frac {R}{\omega L}}\right)^{2}\left({\frac {G}{\omega C}}\right)^{2}} _{{\rm {Very}}\;{\rm {small}}}}\right\}$

或者

$\beta \approx \omega {\sqrt {LC}}\left\{{1+{\frac {1}{8}}\left({{\frac {R}{\omega L}}-{\frac {G}{\omega C}}}\right)^{2}}\right\}$

注意，如果 ${\frac {R}{\omega L}}={\frac {G}{\omega C}}$，則 $\beta \approx \omega {\sqrt {LC}}$

從這裡我們可以觀察到$\beta$ 與$\omega$ 成正比。

因此，無失真傳輸的必要條件是：

RC = LG

這是寬帶同軸電纜網路的基本設計特徵之一。

如果我們將實數項等同起來，我們得到

$\alpha \approx {\sqrt {RG}}$

所以學習代數終究是有原因的！

頻域

訊號分析通常在頻域進行。這告訴我們傳輸線如何影響它們所傳輸訊號的頻譜內容。

為了確定這一點，有必要找到傳輸線方程的傅立葉變換。回想一下

${\frac {\partial ^{2}v}{\partial x^{2}}}=RGv+\left({RC+LG}\right){\frac {\partial v}{\partial t}}+LC{\frac {\partial ^{2}v}{\partial t^{2}}}$

並回想一下（希望如此）傅立葉變換（它將時域轉換為頻域）

$\mathbb {F} \left\{{f\left(t\right)}\right\}=F\left(\omega \right)=\int \limits _{-\infty }^{\infty }{e^{-j\omega t}f\left(t\right)dt}$

為了防止這種分析“爆炸”，我們必須對電壓函式施加一個規定，即它在沿線的無限距離處消失為零。這包括一個基本邊界條件。

${\text{let}}\quad v\to 0\quad {\text{as}}\quad x\to \infty$

這個規定與實際的實驗室實驗相一致。眾所周知，訊號幅度會隨著路徑長度的增加而減小。

同樣，必須施加一個時間邊界條件，即訊號在遙遠的過去某個時間為零，並且在遙遠的未來某個時間也會為零。

${\text{let}}\quad v\to 0\quad {\text{as}}\quad t\to \infty$

儘管工程師在施加這些限制方面沒有困難，但數學純粹主義者卻有些反感。出於這個原因和其他原因，已經開發了其他限制較少的變換。在這種情況下最值得注意的是拉普拉斯變換，它沒有相同的邊界條件。

為了繼續我們的分析，我們必須在做出必要的讓步之後，找到與以下項相對應的傅立葉變換

$\mathbb {F} \left\{v\right\}\quad \quad \quad \mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}\quad \quad \quad \mathbb {F} \left\{{\frac {\partial ^{2}v}{\partial t^{2}}}\right\}$

${\text{Let:}}\quad \quad \quad \mathbb {F} \left\{v\right\}=V$

然後在導數上應用變換，我們得到

$\mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=\int \limits _{-\infty }^{\infty }{e^{-j\omega t}{\frac {\partial v}{\partial t}}dt}$

可以使用分部積分法求解此方程

$\int {u\,dv}=uv-\int {v\,du}$

${\text{let}}\quad u=e^{-j\omega t}\quad \quad \quad \therefore du=-j\omega e^{-j\omega t}$

${\text{and}}\quad dv={\frac {\partial v}{\partial t}}\quad \quad \quad \therefore v=v$

$\therefore \mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=e^{-j\omega t}\left.v\right|_{-\infty }^{\infty }-\int \limits _{-\infty }^{\infty }{v\left({-j\omega e^{-j\omega t}}\right)dt}$

當 t 趨於無窮大時，應用邊界條件使第一項消失。

$\therefore \mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=j\omega \int \limits _{-\infty }^{\infty }{e^{-j\omega t}v\,dt}$

注意，得到的積分只是傅立葉變換。換句話說

$\mathbb {F} \left\{{\frac {\partial v}{\partial t}}\right\}=j\omega \mathbb {F} \left\{v\right\}=j\omega V$

類似地

$\mathbb {F} \left\{{\frac {\partial ^{2}v}{\partial t^{2}}}\right\}=\left({j\omega }\right)^{2}\mathbb {F} \left\{v\right\}=\left({j\omega }\right)^{2}V$

現在我們可以將傳輸線方程寫成頻域形式

${\frac {\partial ^{2}V}{\partial x^{2}}}=RGV+\left({RC+LG}\right)j\omega V+LC\left({j\omega }\right)^{2}V$

其中

$V=V\left(\omega \right)=\mathbb {F} \left\{{v\left(t\right)}\right\}$

重新排列這些項，我們得到

${\frac {\partial ^{2}V}{\partial x^{2}}}=\left[{RG+\left({RC+LG}\right)j\omega +\left({j\omega L}\right)\left({j\omega C}\right)}\right]V$

或者

${\frac {\partial ^{2}V}{\partial x^{2}}}=\left[{\left({R+j\omega L}\right)\left({G+j\omega C}\right)}\right]V$

因為

${\sqrt {\left({R+j\omega L}\right)\left({G+j\omega C}\right)}}=\alpha +j\beta =\gamma$

那麼

${\frac {\partial ^{2}V}{\partial x^{2}}}=\gamma ^{2}V$

或者

${\frac {\partial ^{2}V}{\partial x^{2}}}-\gamma ^{2}V=0$

這代表了頻域中傳輸線方程最一般的形式。現在必須求解此方程以觀察電壓（或電流）如何隨距離和頻率變化。這可以透過假設以下形式的解來完成

$V=\underbrace {Ae^{-\gamma x}} _{{\text{forward}}\;{\text{wave}}}+\underbrace {Be^{\gamma x}} _{{\text{reverse}}\;{\text{wave}}}$

這些項表示訊號沿著傳輸線傳播時呈指數衰減。如果我們忽略任何反射，假設電纜無限長或正確端接，則簡化為

$V=V_{0}e^{-\gamma x}$

為了驗證此假設是否正確，將其代入方程，看看是否出現矛盾。如果沒有矛盾，那麼我們的假設構成一個有效的解。

${\frac {\partial ^{2}}{\partial x^{2}}}V_{0}e^{-\gamma x}-\gamma ^{2}V_{0}e^{-\gamma x}=0$

${\frac {\partial }{\partial x}}\left({-\gamma ^{2}V_{0}e^{-\gamma x}}\right)-\gamma ^{2}V_{0}e^{-\gamma x}=0$

$\gamma ^{2}V_{0}e^{-\gamma x}-\gamma ^{2}V_{0}e^{-\gamma x}=0$

$0=0$

因此我們驗證了假設的解。這告訴我們，在頻域中，傳輸線上的電壓或電流呈指數衰減

$V=V_{0}e^{-\gamma x}$

其中

$\gamma ={\sqrt {\left({R+j\omega }\right)\left({G+j\omega }\right)}}=\left|\gamma \right|\angle \varphi =\alpha +j\beta$

$\gamma ={\text{ propagation}}\;{\text{constant}}$

$\alpha ={\text{ attenuation}}\;{\text{coeficient}}$

$\beta ={\text{phase}}\;{\text{coefficient}}$

在指數形式中，正弦波可以用一個以一定頻率旋轉的單位向量來表示

$e^{j\omega t}=\cos \omega t+j\sin \omega t$

請注意，該函式的幅度為 1，但相位角隨 *t* 的變化而變化。

如果我們令： $V_{0}=e^{j\omega t}$

那麼： $V_{0}=e^{j\omega t}e^{-\gamma x}=e^{j\omega t}e^{-\left({\alpha +j\beta }\right)x}=\underbrace {e^{-\alpha x}} _{{\text{attenuation}}\;vs.\;x}\overbrace {e^{j\left({\omega t-\beta x}\right)}} ^{{\text{phase}}\;vs{\text{.}}\;t\;{\text{and}}\;x}$

這個結果非常有趣，因為它與時域傳輸線方程的解相同。項 ${e^{-\alpha x}}$ 表示指數衰減。隨著長度 *x* 的增加，訊號被衰減。衰減量定義為

以尼培表示的衰減： $N=\left|{\ln e^{-\alpha x}}\right|=\alpha x$

以 dB 表示的衰減： $=20\log e^{-\alpha x}\approx 8.68589\alpha x$

這使我們能夠在知道傳輸線的基本線引數 *R, L, G* 和 *C* 的情況下，確定傳輸線中任何點上的任何頻率的衰減量。

項 ${e^{j\left({\omega t-\beta x}\right)}}$ 表示一個旋轉的單位向量，因為

$e^{j\left({\omega t-\beta x}\right)}=\cos \left({\omega t-\beta x}\right)+j\sin \left({\omega t-\beta x}\right)$

該向量的相位角為 ${\beta x}$ 弧度。

特性阻抗

傳輸線的特性阻抗也稱為衝擊阻抗，不要與它的電阻混淆。即使線路無限長，電訊號仍然會沿著它傳播，儘管電阻趨於無窮大。特性阻抗是由其交流屬性決定的，而不是直流屬性。

回顧我們之前的分析