交換代數/函子、自然變換、泛函箭頭

函子

定義

有兩種型別的函子，協變函子和反變函子。通常，協變函子簡稱為函子。

定義 2.1:

設 ${\mathcal {C}},{\mathcal {D}}$ 是兩個範疇。 協變函子 $F:{\mathcal {C}}\to {\mathcal {D}}$ 將

• 每個物件 $A$ 關聯到 ${\mathcal {C}}$ 中的一個物件 $F(A)$ ${\mathcal {D}}$，並且
• 每個態射 $f:A\to B$ 關聯到 ${\mathcal {C}}$ 中的一個態射 $F(f):F(A)\to F(B)$，

使得以下規則滿足

1. 對於 ${\mathcal {C}}$ 中的所有物件 $A$，我們有 $F(1_{A})=1_{F(A)}$，並且
2. 對於所有態射 $f:A\to B$ 和 $g:B\to C$ 屬於 ${\mathcal {C}}$ ，我們有 $F(g\circ f)=F(g)\circ F(f)$。

定義 2.2:

設 ${\mathcal {C}},{\mathcal {D}}$ 為兩個範疇。一個 逆變函子 $F:{\mathcal {C}}\to {\mathcal {D}}$ 將

• 每個物件 $A$ 關聯到 ${\mathcal {C}}$ 中的一個物件 $F(A)$ ${\mathcal {D}}$，並且
• 每個態射 $f:A\to B$ 對映到 ${\mathcal {C}}$ 中的一個態射 $F(f):F(B)\to F(A)$，

使得以下規則滿足

1. 對於 ${\mathcal {C}}$ 中的所有物件 $A$，我們有 $F(1_{A})=1_{F(A)}$，並且
2. 對於所有態射 $f:A\to B$ 和 $g:B\to C$ 屬於 ${\mathcal {C}}$ ，我們有 $F(g\circ f)=F(f)\circ F(g)$。

遺忘函子

我不確定是否有遺忘函子的精確定義，但事實上，信不信由你，這個概念很容易通過幾個例子來解釋。

例子 2.3:

考慮以同態為態射的群範疇。我們可以定義一個函子，將每個群對映到它的底層集合，並將每個同態對映到它自身作為函式。這是一個從群範疇到集合範疇的函子。由於該函子的目標物件缺少群結構，因此群結構已被遺忘，因此這裡我們處理的是一個遺忘函子。

例子 2.4:

考慮環範疇。請記住，每個環關於加法運算都是一個阿貝爾群。因此，我們可以定義一個從環範疇到群範疇的函子，將每個環對映到它的底層群。這也是一個遺忘函子；它忘記了環的乘法。

自然變換

定義 2.5:

設${\mathcal {C}},{\mathcal {D}}$ 是範疇，並設 $F,G:{\mathcal {C}}\to {\mathcal {D}}$ 是兩個函子。一個 **自然變換** 是 ${\mathcal {D}}$ 中的一族態射 $\eta _{X}:F(X)\to G(X)$，其中 $X$ 取遍 ${\mathcal {C}}$ 中的所有物件，這些態射與 ${\mathcal {C}}$ 中態射 $f:X\to Y$ 在函子 $F$ 和 $G$ 作用下的影像相容；也就是說，下面的圖是可交換的

例 2.6:

設${\mathcal {C}}$ 是所有域的範疇，而${\mathcal {D}}$ 是所有環的範疇。我們定義一個函子

$F:{\mathcal {C}}\to {\mathcal {D}}$

如下：${\mathcal {C}}$ 中的每個物件 $\mathbb {F}$ 將被對映到環 $R_{\mathbb {F} }$，該環由域繼承的加法和乘法組成，其底層集合是元素

$S_{\mathbb {F} }\{\overbrace {1_{\mathbb {F} }+1_{\mathbb {F} }+\cdots +1_{\mathbb {F} }} ^{n{\text{ times}}}|n\in \mathbb {N} _{0}\}\cup \{\overbrace {-1_{\mathbb {F} }-1_{\mathbb {F} }-\cdots -1_{\mathbb {F} }} ^{n{\text{ times}}}|n\in \mathbb {N} \}$,

其中 $1_{\mathbb {F} }$ 是域 $\mathbb {F}$ 的單位元。 任何域的態射 $f:\mathbb {F} \to \mathbb {G}$ 將被對映到限制 $f\upharpoonright _{S_{\mathbb {F} }}$； 注意，這是定義良好的（即，對映到與 $\mathbb {G}$ 相關的物件，在函子 $F$ 下），因為

$f(1_{\mathbb {F} }+1_{\mathbb {F} }+\cdots +1_{\mathbb {F} })=f(1_{\mathbb {F} })+f(1_{\mathbb {F} })+\cdots +f(1_{\mathbb {F} })=1_{\mathbb {G} }+1_{\mathbb {G} }+\cdots +1_{\mathbb {G} }$

以及

$f(-1_{\mathbb {F} }-1_{\mathbb {F} }-\cdots -1_{\mathbb {F} })=-f(1_{\mathbb {F} })-f(1_{\mathbb {F} })-\cdots -f(1_{\mathbb {F} })=-1_{\mathbb {G} }-1_{\mathbb {G} }-\cdots -1_{\mathbb {G} }$,

其中 $1_{\mathbb {G} }$ 是域 $\mathbb {G}$ 的單位。

我們進一步定義了一個函子

$G:{\mathcal {C}}\to {\mathcal {D}}$,

將每個域 $\mathbb {F}$ 對映到其關聯的 素域 $\mathbb {F} _{\text{prime}}$，將其視為一個環，然後再次限制態射，即，將每個態射 $f:\mathbb {F} \to \mathbb {G}$ 對映到 $f\upharpoonright _{\mathbb {F} _{\text{prime}}}$（這根據與上面相同的計算以及注意到 $f$ 是域態射，將逆對映到逆而定義）。

在這個設定中，對映

$\eta _{\mathbb {F} }:R_{\mathbb {F} }\to \mathbb {F} _{\text{prime}}$,

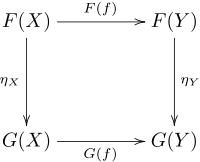
由包含給出，形成從 $F$ 到 $G$ 的自然變換；這可以透過直接檢查交換圖來驗證。

泛箭頭

定義 2.7（泛箭頭）:

設 ${\mathcal {C}},{\mathcal {D}}$ 為範疇，設 $F:{\mathcal {C}}\to {\mathcal {D}}$ 為一個函子，設 $Y$ 為 ${\mathcal {D}}$ 中的一個物件。**泛對映**是一個態射 $g:Y\to F(X)$，其中 $X$ 是 ${\mathcal {C}}$ 中的一個固定物件，使得對於 ${\mathcal {C}}$ 中的任何其他物件 $Z$ 和態射 $h:Y\to F(Z)$，都存在唯一態射 $f:X\to Z$ 使得該圖

可交換。