計算機系統工程/馬爾可夫模型

馬爾可夫模型

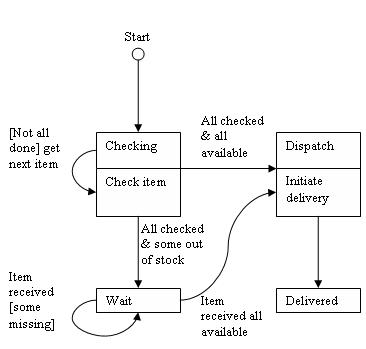
狀態圖描述了系統的行為。它們描述了系統的所有可能狀態（UML 中的物件）以及狀態如何隨著到達系統的事件（物件）而改變。

例如：

需要注意的是，馬爾可夫模型將狀態轉換視為一個隨機過程。

假設每個狀態由一個隨機變數定義。隨機變數集 {x_n} 構成一個馬爾可夫鏈，如果下一個值（狀態）為 x_n+1 的機率僅取決於當前值（狀態）x_n，而與任何先前值無關。整個先前歷史對未來行為的影響都總結在當前狀態中。對於“離散時間”馬爾可夫鏈，轉換隻能在整數 1、2、3 … 發生。對於“連續時間”馬爾可夫鏈，轉換可以在任何時間發生。這很重要，因為過去的歷史完全由當前狀態指定，我們也不能指定程序在當前狀態中停留了多長時間。

分析：P(x(t_n+1) = x_n+1 | x(t_n) = x_n, x(t_n-1) = x_n-1, … x(t₁) = x₁) = P(x(t_n+1) = x_n+1 | x(t_n) = x_n)，其中 t₁ < t₂ < … < t_n < t_n+1 且 x₁、x₂、…、x_n 處於某個離散狀態空間中。

考慮離散時間馬爾可夫鏈

觀察：離開每個城市的機率之和為 1。

P(x_n = j | x₁ = i₁, x₂ = i₂, …, x_n-1 = i_n-1) = P(x_n = j | x_n-1 = i_n-1)。

P(x_n = j | x_n-1 = i_n-1) 是一個一步轉移機率。該機率從一步 n-1 的狀態 E=i 轉移到一步 n 的狀態 E=j。

令 P_ij(n) = 系統在 n-1 步內從狀態 E_i 轉移到狀態 E_j 的機率。然後，是系統在一步內從狀態 E_i 轉移到狀態 E_k，然後在 n-1 步內從狀態 E_k 轉移到狀態 E_j 的機率。這稱為查普曼-科爾莫哥洛夫方程。

令 P(n) 為矩陣。每個條目都是 P_ij(n)。如果這是一個 n 步轉移機率矩陣，那麼

(如果與 n 無關，則稱為齊次)

定義 P_ij = P(x_n = j | x_n-1 = i) 作為系統在狀態 E_i 時轉移到下一個狀態 E_j 的機率。這稱為一步轉移機率集。

示例：P₀₀ = 0，P₀₁ = ¾，P₀₂ = ¼，P₁₂ = ¾

以矩陣形式

令 π_j = P(x_n = j) 為系統在步 n 時處於狀態 j 的機率。在我們的示例中，

步 n+1 時處於狀態 j 的機率是在步 n 時處於狀態 i 並在一步內轉移到狀態 j 的機率。

以向量形式

特別地，

例如：令 Π(0) = [0,1,0]，從哥倫比亞開始。

經過很長時間後，令

因此，

示例

觀察

(1) 和 (2) 之和為負 (3)，因此方程之間存線上性相關性，因此沒有唯一解。我們還知道 π₀ + π₁ + π₂ = 1（即系統必須處於某個狀態）。這稱為歸一化條件。

現在求解

觀察

這就像擲硬幣，其中 r = 正面機率，1-r = 反面機率。因此，P(正好有 m 個正面的序列) = r^m (1-r)。

一個程序在狀態 i 中停留多長時間？

假設該程序進入狀態 E_i。然後，在下一步中停留在狀態 E_i 的機率是 P_ii。程序在下一步中離開 E_i 的機率是 1-P_ii。每一步都是獨立的，所以 P(系統在剛進入狀態 E_i 後正好再停留 m 步) = (1-P_ii) P_ii^m。換句話說，該程序以 m*( P_ii P_ii P_ii …P_ii) 的機率停留 m 步，並在第 m+1 步離開狀態。

幾何分佈

狀態 E_i 中的平均時間是 E(在狀態 E 中的時間)

現在，, 因此

因此，

簡而言之，程序在離開狀態之前停留的平均時間是離開機率的倒數。

假設觀察狀態 i k 步，並且該系統沒有改變狀態。程序在下一步中不離開狀態的機率是多少？令 y = 到第一次離開的步數。

因此，該程序是無記憶的——正如我們所知。

連續時間馬爾可夫鏈

P(x(t_n+1) = j | x(t_n) = i_n … x(t₀) = i₀) = P(x(t_n+1) = j | x(t_n) = i_n)

回想一下，馬爾可夫鏈是無記憶的，因此轉換不取決於程序在給定狀態中停留的時間。

令 τ_i = 在狀態 i 中停留的時間。P(τ_i > s+t | τ_i > s) = h(t)，它只是 t 的函式（不是 s）。該函式顯示了程序在狀態中停留的時間。

因此，指數是唯一滿足此條件的連續分佈。同樣，如果我們設定 s、t = 0，那麼 P(τ_i >0) = 1，並且

定義時間相關的轉移機率

現在，考慮時間 s ≤ u ≤ t。為了從時間 s 的狀態 E_i 轉移到時間 t 的狀態 E_j，程序必須在時間 u 時經過某個狀態。因此，

這是查普曼-科爾莫哥洛夫方程，與離散情況完全類似，但難以直接使用。

回想一下

在查普曼-科爾莫哥洛夫方程中，將 t+h 代入 t

除以 h，取 h 趨近於 0，u 趨近於 t 的極限

這稱為科爾莫哥洛夫的前向方程。

此外，

是科爾莫哥洛夫的後向方程。

如果時間齊次轉移機率不依賴於初始時間 t，而只依賴於間隔 h，則 q_ij(t) = q_ij 且 q_j(t) = q_j 且 = P_ij(h)，那麼

狀態轉移機率和初始分佈決定了馬爾可夫鏈的所有屬性。觀察

除以 h，取 h 趨近於 0，v 趨近於 t 的極限

.

如果時間齊次

狀態分類

回想一下

如果系統有正機率不會返回到該狀態，則該狀態是瞬態狀態。令 X_ji = 從狀態 j 開始訪問狀態 i 的次數。X_ji 的期望值 E(X_ji) 為

如果 E(X_ji) 是有限的，則狀態 i 是瞬態狀態。這意味著 P_ji(n) 在 n 趨近於無窮大時趨近於 0。

如果從狀態 j 出發，一個過程以 1 的機率返回到狀態 i，那麼狀態 i 就是迴圈狀態。此外，它是無限的。

考慮從狀態 j 到達狀態 i 所需的時間，對於一個迴圈鏈。令 f_ij(n) = 在 n 步內從 i 首次訪問 j 的機率。令 f_ii(n) = 在 n 步內從 i 首次返回 i 的機率。那麼，從狀態 i 出發訪問 j 的機率為

如果 f_ii = 1，則狀態 i 是迴圈狀態，如果 f_ii < 1，則狀態 i 是瞬態狀態。如果 f_ii = 1，那麼平均迴圈時間為。如果 是有限的，則狀態稱為非零迴圈狀態，如果 是無限的，則狀態稱為零迴圈狀態。

對於迴圈狀態 i，狀態 i 的週期 是使得 為正整數的集合 n 的最大公約數。如果 = 1，則系統是無週期的，如果 > 1，則系統是有周期的。

當且僅當 P_ii = 1 時，系統是吸收的。

如果每個狀態都可以在有限步內從其他任何狀態到達，那麼馬爾可夫鏈是不可約的。不可約馬爾可夫鏈的所有狀態都是相同型別的。在一個無週期馬爾可夫鏈中，所有狀態都是無週期的。如果一個狀態具有周期 d，那麼所有狀態都具有相同的週期 d。

連續時間馬爾可夫鏈

令 = 隨機變數 = 在狀態 i 中的時間。馬爾可夫性質意味著過渡的機率不能依賴於系統在一個狀態中停留的時間。

現在對於 s=0，我們有

s = t = 0 再次需要

現在，

因此，在狀態 i 中的時間呈指數分佈，引數為，它可能取決於狀態。

我們已經看到 = 在狀態 i 中的時間，並且令 t 是時間 h 的一個很小的增量

最後一個等式是系統在下一個時間增量 h 內離開狀態的機率。這可以用泰勒級數表示

將狀態編號為 0,1…，令 = 過渡到更高編號狀態（出生）的機率。令 = 過渡到較低編號狀態（死亡）的機率。只允許過渡到下一個更高或更低編號狀態（或停留在相同狀態）。這被稱為生死過程。

令 P(n=k,t) = 在時間 t 處於狀態 k 的機率。考慮一個過程如何在時間 t+h 進入狀態 n=k。

對於出生：必須處於狀態 n=k-1，並且發生出生事件。

對於死亡：必須處於狀態 n=k+1，並且發生死亡事件。

如果沒有出生和死亡：必須在時間 t 處於狀態 n=k。

平衡方程

流量平衡

平衡平衡方程可以透過下面所示的狀態轉換速率圖直觀地推匯出來。

這類似於我們已經見過的狀態轉換圖。在平衡狀態下，進入一個狀態的機率流率必須等於從該狀態流出的機率流率。因此

求解平衡方程

數量 稱為“交通強度”，通常用 表示。

回想一下，如果作業到達的速度快於處理的速度，佇列將不穩定。因此

正如我們將看到的，決定了佇列中大多數感興趣的屬性。請注意，它是透過到達率和服務率的比率來確定的，而不是它們的絕對值。具有相同交通強度的佇列可以預期具有相似的屬性，即使它們的到達率或服務率可能大不相同。

常數 P(0) 是使用歸一化要求確定的，如下所示

請注意最後一個方程與幾何分佈的相似性

這是佇列中有 k 個作業的機率，如下所示

佇列中至少有 1 個作業的機率為。這是伺服器的利用率，即伺服器繁忙的機率。

佇列中的數量

佇列中作業的平均數量為

求和是使用以下技巧進行評估的：注意

現在由於導數的和是和的導數，

這在 從 0 增加到 1 時顯示如下

佇列中作業數量超過 r 的機率為

這在幾個 值時顯示如下

請注意，P(n≥r) 在 中呈幾何下降。還要記住， 是伺服器的利用率。因此，對於利用率低的伺服器（ 較小），佇列中存在大量作業的可能性很小。對於利用率高的伺服器（ 接近 1），等待服務的作業數量多的可能性要高得多。

令 T = 平均等待時間，T_n = 抵達 n 的等待時間，系統中有 n-1 個客戶，x_i = 第 i 個客戶的服務需求（i = 1,2,…,n），x_o = 正在服務的客戶的剩餘服務時間，以及 x_n = 第 n+1 個客戶的服務需求。