計算機系統工程/機率
一個實驗,真實的或想象的,可以用三個特性來描述。這些是
- 1. 一組結果
- 2. 將這些結果分組為類別
- 3. 這些類別出現的相對頻率。
例如,拋硬幣是一個實驗,其結果要麼是正面要麼是反面。一組結果將是正面 (H) 或反面 (T)。那麼正面的相對頻率將是在大量拋擲中正面出現的次數。
(1)
如果將成對的拋擲作為實驗的結果,則結果集將是 HH、HT、TH 和 TT。這些可以分為三類:2 個正面、2 個反面和 1 個正面和 1 個反面。假設硬幣是公平的,則 1 個正面和 1 個反面的類別的相對頻率將是其他兩類的兩倍。
在機率論中,“樣本空間”,用 S 表示,對應於結果集,每個可能的結果都是 S 的一個元素。“事件”對應於一類結果,“機率”是事件相對頻率的度量。這可以解釋為如果實驗重複多次,事件發生的次數佔總次數的比例。
(2)
形式上,機率測度滿足以下性質
*1. For any event A, 0≤P(A)≤1 *2. P(S) = 1 *3. If A and B are mutually exclusive events then P(A+B)=P(A)+P(B). (3)
A + B 是樣本空間中包含事件 A 或 B 或兩者都包含的元素的集合。事件 A 可以描述為
A = {ω: ω satisfies membership property for A} (4)
其中 ω 是樣本空間的成員,ωєS。這讀作:“A 是 ω 的集合,其中 ω 滿足 A 的成員屬性。”類似地,引入集合論符號表示事件的補集、並集和交集,令
AC = {ω: ω not in A}
= complement of A
A + B = {ω: ω in A or B or both}
= union of A and B* (5)
A,B = {ω: ω in both A and B}
= intersection of A and B*
Ø = SC = null event = no sample points since all sample points are in S
- 在集合論符號中,“+”和“U”都用於表示兩個集合的並集。類似地,交集用“,”、“∩”、“∙”表示,或者有時透過將符號並排寫來表示。“+”和“∙”暗示了加法和乘法的算術運算,集合的並集和交集運算與此類似。但是,不應該將它們混淆。一個應用於集合,另一個應用於數字。
這些在下圖的韋恩圖中進行了說明。正方形中的點表示樣本空間 S,封閉迴圈中的點表示事件。
在 I 中注意
S = A + AC (6)
並且 AC 和 A 中的點是互斥的。因此,使用 (3)
P(S)= P(AC + A) (7)
= P(AC)+P(A)
但 P(S) = 1,因此
P(AC) = 1 - P(A) (8)
在 IV 中,A 和 B 中的點不是互斥的。在這種情況下
(9)
(9) 中的最後一項是必要的,因為前兩項都包含 A、B 中的點,但我們只想在 A+B 中計算這些點一次。
條件機率
如果事件 B 發生,“條件機率”A 也發生的機率 P(A|B)(讀作:“給定 B 時 A 的機率”)定義為
(10)
這給出了 B 中也屬於 A 的點的分數。實際上,有了 B 的知識,我們可以建立一個新的樣本空間,其中僅包含 B 中的點,然後查詢 A 中屬於 B 的點的相對頻率。
如果
P(A,B) = P(A) P(B) (11)
則稱 A 和 B 是獨立的。
(12)
注意,如果 A 和 B 是獨立的,則
A + AC = S (13) A, AC = Ø
這意味著 B 的知識不會告訴我們 A 發生的頻率。正如我們在 (5) 和 (6) 中提到的,A 和 AC 覆蓋 S 並且是互斥的。
B = B,A + B, AC (14)
因此
P(B) = P(B,A + B, AC) (15) = P(B,A) + P(B, AC)
由 (10)
P(B,A) = P(B|A) P(A) (16)
和
P(B,AC) = P(B|AC) P(AC) (17)
因此
P(B) = P(B|A) P(A) + P(B|AC) P(AC) (18)
如果事件 Ai,i = 1,2…n 是互斥且窮舉的,即
A1 + A2 +… An = S (19) Ai,Aj = Ø for all i ≠ j
則 (15) 和 (18) 可以更一般地寫成
(20)
和
(21)
這就是“全機率公式”。另一個有用的關係來自 (10),即“貝葉斯定理”
(22)
然而,由 (18)
P(B) = P(B|A)P(A) + P(B|AC)P(AC) (23)
因此
(24)
因此,如果我們知道事件 A 的機率 P(A) 和 A 對 B 的機率的影響 P(B|A),則可以計算 B 對 A 的機率的影響 P(A|B)。
一個例子
貝葉斯定理在元件測試中可能有一些非直觀的結論。
假設我們有一種測試記憶體晶片的方法。如果晶片損壞 (B),則測試 95% 的時間會顯示損壞 (T)。
P(T|B) = .95 (25)
如果晶片完好 (BC),則測試 95% 的時間會顯示完好 (TC)。
P(TC|BC) = .95 (26)
另外,假設 1% 的晶片損壞。
P(B) = .01 (27)
測試結果為損壞的晶片中,有多少百分比是真正損壞的?即,P(B|T) 是多少?應用 (24) 我們有
(28)
由 (8)
P(BC) = 1 – P(B) = .99 P(T| BC) = 1 – P(TC|BC) = .05 (29)
這意味著 B 的知識不會告訴我們 A 發生的頻率。正如我們在 (5) 和 (6) 中提到的,A 和 AC 覆蓋 S 並且是互斥的。
(30)
此外,測試結果為完好的晶片中,完好晶片的機率為
(31)
並且由 (8)
P(TC|B) = 1 - P(T|B) = .05 (32)
這意味著 B 的知識不會告訴我們 A 發生的頻率。正如我們在 (5) 和 (6) 中提到的,A 和 AC 覆蓋 S 並且是互斥的。
(33)
因此,幾乎所有測試結果為完好的晶片都是完好的,但只有 16% 測試結果為損壞的晶片確實有缺陷。該測試並沒有我們希望的那樣有辨識力。
組合和排列
N 個可區分的物件可以以 N! 種不同的方式排序(排列)。這很容易透過觀察得出,任何 N 個物件都可以放在第一個位置;其餘 n-1 個物件中的任何一個都可以放在第二個位置;依此類推,直到只有一個物件可以放在最後一個位置。
更一般地,可以從 N 個物件的集合中選擇 r 個物件的集合,有 N(N—1) (N—2) ... (N—r+1) = N! / (N—r)! 種不同的方式。這是不放回抽樣。如果 r =N,則有 N! 個集合,每個集合僅僅是 N 個物件的排序。
一旦選擇,集合中的 r 個物件可以在不改變集合組成的情況下以 r! 種不同的方式排序。每個排序對應於 N! / (N—r)! 抽樣中的另一個抽樣。因此,如果只考慮所選物件而不考慮它們的順序,則有
種不同的方式從 N 個物件的集合中選擇 r 個物件。這稱為從 N 個物件中取 r 個物件的組合,並使用特殊的符號表示
注意,對於 r = N,
以及對於 r = 1,
組合也可以被認為是將物件劃分為分別包含 r 個物件和 (N—r) 個物件的組的方式的數量。這自然地導致了 N 個物件可以被劃分為 k 個組,第 i 個組包含 ni 個物件,i = 1,2,…k 且 N = Σni 的擴充套件
種不同的方式。
隨機變數是一個變數,其值取決於實驗的結果。因此,隨機變數實際上是一個函式,它將數值分配給樣本空間 S 中的每個事件。在實踐中,隨機變數分配給事件的值被選擇為具有某種物理意義。例如,如果我們對拋硬幣實驗下注,正面贏 1.00 美元,反面輸 0.50 美元,則隨機變數 X 可以分配以下值
(34)
其中 ω 是實驗的結果。
通常,我們感興趣的是隨機變數取特定值的機率。
P(X = x) (35)
這是樣本空間的成員 ω(其中 X(ω) = x)出現的相對頻率之和。也就是說
P(X = x) = relative frequency for which X(ω) = x. (36)
如果硬幣是公平的(即正面和反面出現的可能性相同)在 (34) 中,則
P(X = 1) = 1/2 P(X = -.5) = 1/2 (37)
機率的另一種有用表示是“機率分佈函式”,
(38)
這也稱為“累積分佈函式”。它在 (34) 中顯示如下
注意,由於 S 中的每個點都由隨機變數對映到實數線上
P ( X ≤ -∞ ) = 0 P ( X ≤ ∞ ) = 1 P ( X ≤ x ) ≥ 0, for all x on the real line (39)
此外,對於實數線上的兩個點 a 和 b
P ( X ≤ b) – P (X ≤ a ) = P ( a < X ≤ b ), for a < b (40)
和
P ( X ≤ b) ≥ P (X ≤ a ), for a ≤ b (41)
用於描述拋硬幣實驗的隨機變數只能取有限數量的值(在這種情況下為 2:+1 和 -0.5)。這稱為離散隨機變數。用於描述其他實驗(例如,兩件事發生之間的時間)的隨機變數可能更適當地具有連續的值範圍。這種“連續隨機變數”具有連續分佈函式,我們用以下表示
F ( x ) = P ( X ≤ x ) (42)
與離散情況一樣,F(x) 是一個非遞減函式,並且
0 ≤ F(x) ≤ 1 , for all x. (43)
這種隨機變數的一個常見例子是指數分佈的隨機變數
(44)
其中 λ < 0。這在下圖中顯示
出於計算目的,另一個函式“機率密度函式”通常比分佈函式更方便。假設導數存在,則將其定義為分佈函式的導數。
(45)
由於 F(x) 是非遞減的,因此 f(x) ≥ 0。此外,由 (45)
(46)
和
1 = F(∞) = (47)
和
P ( a ≤ x ≤ b ) = F ( b ) – F ( a ) = (48)
因此,f ( x ) 是一個函式,當在其區間上積分時,給出隨機變數 X 落在該區間內的機率。
注意,由 (47) 定義的 f ( x ) 曲線下的面積為 1。因此,令 Δx 為一個小區間
f ( x ) Δx
是一個高為 f ( x )、寬為 Δx 的矩形。然後 f ( x ) Δx 近似於 f ( x ) 曲線在 x 到 x + Δx 範圍內曲線下的面積。
當 Δx 變為零時(用 dx 表示:lim Δx 0 Δx = dx),該近似值變得精確。因此,通常將 f ( x ) dx 視為 X“等於”x 的機率是有用的。
f(x)dx = P(X ‘=’ x) (49)
嚴格來說,它是 X 落在點 x 周圍的一個非常小的區間內的機率。
在對計算機系統進行建模時,我們通常對系統中的作業數量、等待時間和服務需求等事物感興趣,這些事物只能取非負值。用於描述這些量的隨機變數只能取非負值
F(x) = P(X ≤ x) = 0, for x < 0 (50)
這通常使處理它們的數學運算稍微簡單一些。在下文中,我們將假設隨機變數是非負的,但這可以很容易地擴充套件到更一般的情況。
指數分佈的隨機變數 (44) 是一個非負隨機變數。對於 x ≥ 0,它的導數在任何地方都定義為
= λe-λx (51)
期望值
儘管機率分佈函式描述了大量實驗的綜合行為,但它通常過於複雜,無法用於比較替代實驗的結果。我們需要一個單一的數字,“品質因數”,來表示實驗的結果。這由隨機變數的“期望值”、“平均值”或“均值”(這三個術語是同義詞)提供。如果 X 是一個隨機變數,則符號 E(X) 和
都用於表示其期望值。它被定義為隨機變數的值與其實驗給出此結果的頻率的乘積之和。對於離散情況,這是
(52)
在連續情況下
(53)
在隨機變數取整數值的重要情況下,(52) 變為
(54)
注意,這可以改寫為
(55)
每列中各項的總和為 kP(N = k),其中 k = 1, 2, … 是列。但(55)的第一行只是 N > 0 的機率,第二行是 N > 1 的機率,依此類推。因此,我們也可以寫成
(56)
根據分佈函式 (38),我們有
P ( N > k ) = 1 – P ( N ≤ k ) (57)
給出
(58)
由於分佈函式 P ( N ≤ k ) 通常比密度 P ( N = k ) 更容易測量或估計,因此 (58) 提供了一種計算隨機變數平均值的便捷方法。
類似的結果在連續情況下也成立
(59)
這很容易透過分部積分 (59) 來證明
(60)
回想一下 F ( ∞ ) = 1 並且
(61)
這簡化為
(62)
由於每個隨機變數都與一個數字相關聯,因此可以對其進行數值運算(加、乘等),並且可以像普通數字一樣在其上定義任意函式。令 g(X) 是定義在隨機變數 X 上的函式。期望值的定義 (52, 53) 可以擴充套件到給出 g(X) 的期望值:E(g(X))
E(g(X)) = (63)
如果 X 是離散的,或者
E(g(X)) = (64)
在連續情況下。
兩個隨機變數 X 和 Y 的和的期望值為
E ( X + Y ) = (65)
使用 (16),我們注意到
P ( X=x, Y=y ) = P ( X=x / Y=y ) P ( Y=y ) (66)
以及
P (X=x, Y=y ) = P ( Y=y, X=x ) = P (Y=y / X=x ) P ( X=x ) (67)
因此
E ( X + Y ) = (68)
現在
(69a)
和
(69b)
因此
E ( X+Y ) = E ( X ) + E ( Y ) (70)
此外,如果 X 和 Y 是獨立的
E( X,Y ) = (71)
因為 X 和 Y 是獨立的。因此
E ( X,Y ) = = E ( X ) E ( Y ) (72)
結果 (70 和 72) 也適用於 X 和 Y 是連續隨機變數的情況。
回想一下 (21),
P (X=xi) = (73)
根據定義 (52)
E(X) = (74)
因此
E (X) = (75)
根據 (52) 的類比,(75) 中的第二個和被定義為給定 Y=yj 時 X 的條件期望值。這通常寫成 E(X/Y)
E(X/Y) = E(X/ Y=yj) = (76)
因此 (75) 為
E(X) = (77)
但這只是 E(X/Y) 的期望值。
因此
E(X) = E( E(X/Y) ) (78)
同樣,如果 X 是連續隨機變數,這也適用。
方差
如前所述,密度函式下的面積為 1。如果將此“面積”剪下並放在一個支點上,則期望值是它將平衡的點。
由於與力學的關係,期望值通常稱為隨機變數的**一階矩**。
另一個用於描述隨機變數的有用品質因數是其“二階矩”,定義為
E (X2) = (79)
對於離散情況,以及
E (X2) = (80)
對於連續情況。請注意,它是隨機變數平方的期望值。
我們通常不直接使用二階矩,而是更感興趣的是找到“關於均值的二階矩”或“二階中心矩”。對於離散情況,這是
(81)
回想一下,第一個和是二階矩 (79),第二個是均值 (52),第三個根據定義 (3) 必須為 1,這變成了
(82)
類似地,對於連續情況
(83)
二階中心矩提供了隨機變數的值圍繞均值聚集的緊密程度的度量。例如,如果隨機變數只能取一個值 α,則
P(X=x) = 1 for x= α (84) 0 for x≠ α
和
(85)
和
(86)
由此可見,根據 (82),
(87)
對於前面提到的指數分佈隨機變數 (44, 51)
(88)
和
(89)
因此
(90)
二階中心矩實際上說明了隨機變數中存在多少變化。恰如其分地,它通常被稱為隨機變數的“方差”,Var(X),並用符號 σ2 表示
(91)
請注意,由於 σ2 是隨機變數平方的期望值,因此它始終為正。
此外,隨機變數的標準差,用符號 σ 表示,定義為方差的平方根
(92)
請注意,這與隨機變數和均值具有相同的度量單位。
儘管方差和標準差提供了對隨機變數值中預期變化量的度量,但如果隨機變數具有較大的均值,則給定數量的變化通常不如它較小時重要。“變異係數”C 提供了一種表達變化量與隨機變數均值的關係的方法。它被定義為
(93)
請注意,對於確定性隨機變數 (84, 87),σ = σ2 = 0,因此
C = 0 (94)
對於指數隨機變數 (44, 90)
(95)
因此,在 (93) 中使用 (88) 和 (89)
(96)
三階中心矩
三階中心矩 M3 定義為
和
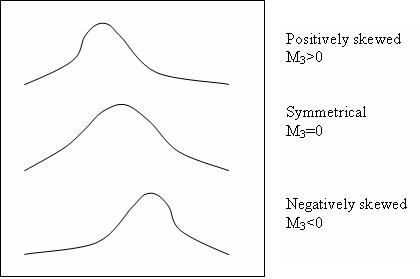
分別用於離散和連續情況。這提供了分佈對稱性的度量。
對於 M3 = 0,分佈是對稱的。對於 M3 > 0,它是正偏的,對於 M3 < 0,它是負偏的。如下所示。
四階中心矩
四階中心矩 M4 定義為
和
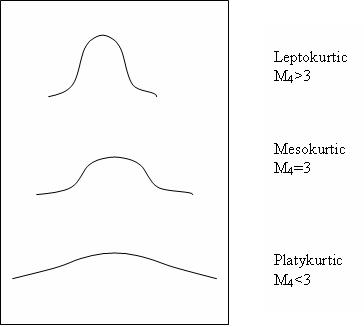
分別用於離散和連續情況,測量分佈的平坦度或峰值。它是比方差更靈敏的分佈擴充套件度量。
下圖顯示了具有相同方差 σ2 = 1 和 M4 > 3、M4 = 3 和 M4 < 3 的分佈。對於 M4 > 3,分佈是“高而瘦的”;對於 M4 < 3,它是“平的”,對於 M4 = 3,它是“中等”。
參考文獻
- 1. Kleinrock,Leonard,排隊系統卷 1:理論。John Wiley,紐約,1975 年。