計算機系統工程/排隊系統模型
佇列正式定義為由一個伺服器和一個等待線組成,用於為需要服務於伺服器的客戶提供服務。每個客戶都加入等待線的末尾。當等待線最前面的客戶得到服務時,他們後面的客戶會逐漸移動到等待線的最前面。客戶一旦從伺服器那裡獲得所需的服務,就會離開,伺服器開始為等待線中的下一個客戶提供服務。如下圖所示。
許多自然系統都可以用這種方式來描述。例如,在一家雜貨店裡,購物者排隊等候收銀員結賬。這裡,購物者是顧客,收銀員是伺服器,而收銀員為每個購物者結賬所花費的時間是該購物者的服務需求。同樣,在銀行裡,顧客排隊等候出納員,他們完成自己的交易。在這種情況下,所有出納員都可以使用單一等待線。在計算機系統中,顧客是提交用於處理的任務,伺服器是 CPU 或磁碟控制器等裝置,而服務需求是任務在該裝置上花費的時間。例如,如果伺服器是 CPU,則服務需求是任務將獲得的處理量;如果伺服器是磁碟控制器,則服務需求是執行磁碟讀或寫操作的時間。
任務加入等待線並進入佇列之間的時間以及每個任務所需的處理時間都是由隨機變數給出的。到達率是每秒到達任務的平均數量。這用 λ 表示,因此 λ 是到達之間平均時間。
and are both used to represent the average service requirement. In a large interval T the expected number of arrivals is
在 T 時間內的預期到達數量 =
這些任務的平均服務需求為 μ。因此,伺服器提供的預期服務量為
伺服器繁忙的時間比例是它的利用率。這是
量 ρ 被稱為佇列的“交通強度”,用特殊符號 ρ 表示
注意,如果 ρ 大於 1,則到達的任務比在 T 時間內可以處理的任務多。在這種情況下,等待線中任務的數量會無限增長,佇列不穩定。只有當到達過程和服務需求是確定性的時,佇列才是穩定的。由於任務到達和/或服務需求的波動,非確定性佇列必須有 ρ < 1 才能保持穩定。對於 ρ < 1,ρ 是伺服器繁忙的機率(即時間比例)。因此,1 - ρ 是它空閒的機率。
在研究佇列時,最重要的是要問以下問題
• How long must a job wait before receiving service? • How long will it stay in the queue before leaving (waiting time plus service time)? • How many jobs are in the queue? • What is the utilization of the server? (i.e. What fraction of the time is the server busy?)
在有限人口模型中,有固定數量 N 個任務。任務從某個來源到達佇列,並在完成服務需求後返回到該來源。如下圖所示
如果佇列中有 k 個任務,則來源中有 N-k 個任務。我們假設任務在來源中等待呈指數分佈的時間,平均時間為 θ,然後返回到佇列,並且彼此獨立。如果來源中有 (N-k) 個任務,那麼它們會建立一個泊松輸入過程到佇列,速率為
有限人口 M/M/1 佇列的狀態轉移圖如下所示。
請注意,當佇列中有 N 個任務時,來源中沒有任務,λN = 0。因此,佇列狀態 n > N 的機率為零。
歸一化方程變為
因此
或
它描述了平均排隊長度、平均到達率和平均排隊等待時間之間的關係。這個定理對於任何處於穩態條件的排隊系統都適用。
一個客戶在系統中花費時間 w,在此期間,客戶以穩定的速度到達。這必須是系統中客戶的平均數量(否則數量要麼增加要麼減少)。
形式上,
在具有不同型別客戶的系統中,Little 公式分別適用於每種型別。例如,在優先順序系統中,
考慮僅包含伺服器的系統
Comten 網路處理器 資料包:2048B = 16,384 位 線路:56Kbps
292.5ms = .2924 秒 ≈ .3 秒
假設我們想每秒傳送 7 個數據包的總量
但是,請記住,在 100% 利用率下存在延遲,
因此,我們可能實際上想使用 4 條線路來進一步降低利用率。
任務在佇列中花費的平均時間可以透過 Little 公式求得
這稱為佇列的“響應時間”,用 T 表示。因此,使用 Wq = T - 1/μ,我們得到
或
如下圖所示,隨著 ρ 從 0 增加到 1,響應時間(和系統中的數量)也隨之增加。
請注意,響應時間(和系統中的數量)在伺服器利用率小於 50%(即 ρ < 0.5)時保持相當平穩,並且當伺服器接近 100% 利用率時急劇上升。這種現象是幾乎所有排隊系統的特徵。當我們試圖讓伺服器接近其容量(即 ρ 接近 1)時,響應時間和佇列中的數量會變得非常大。對於 ρ > 1,系統變得不穩定,佇列中的數量和響應時間會無限增長。
停等協議會佔用傳輸線路,因為線路上的時間用於傳送資料包,然後會延遲,直到收到確認。
線路 = 伺服器等待線路 = 要在站點的訊息傳送服務時間 = 傳輸時間
或者,使用停止並等待,服務時間 = 週期時間。
為了提高線路速度,必須縮短服務時間。
如果超過 m 個伺服器繁忙,m 個伺服器會拒絕到達。
請注意,此 m 伺服器丟失系統中沒有封閉式表示式。值可以從表格中計算出來。此係統通常用於根據呼叫率和呼叫持續時間來確定電話通道的大小。
我們對 M/M/1 佇列的討論可以透過允許到達率和服務率依賴於佇列狀態來推廣。也就是說,到達過程是引數為 的泊松過程,服務要求是引數為 的指數分佈。下標 n 指的是佇列中的作業數。如果佇列狀態為 n=k,則到達的機率為
並且離開的機率(假設佇列不為空)為
到達或離開的機率僅透過引數 和 依賴於佇列狀態。
由於泊松過程的無記憶性,在時間 t 佇列處於狀態 n=k 且在給定佇列在間隔開始時處於狀態 k 的情況下,在間隔 h 內有到達或離開的機率是獨立的。因此,下面的狀態轉移圖描述了馬爾可夫鏈。
透過觀察發現的平衡方程要求“機率流出”速率等於流入速率
並且歸一化方程又是
這些方程可以透過考慮簡單 M/M/1 佇列中間隔 h 內到達、離開和無變化的機率來更正式地找到。
以及對於 k=l,
將 P(1) 替換得到
以及一般情況下,
使用歸一化方程找到常數 P(0)。將 P(k) 替換得到
或
結合得到一般解
Kleinrock 討論了平衡狀態下生死佇列的幾種變體。兩種情況在對計算機系統建模時特別有用。它們是“無限伺服器佇列”和“有限種群模型”。
在無限伺服器佇列中,當作業到達佇列時,總會有一個空閒的伺服器。
如果佇列中有 2 個作業,則服務率為 (我們可以將其視為 2 個泊松服務過程的疊加,每個過程的速率為 ),並且如果佇列處於狀態 n=k,則服務率為 。請注意,這意味著服務完成之間的平均時間為
當佇列狀態為 n=k 時。很明顯,這個排隊系統也可以解釋為有一個單一伺服器,當有更多作業等待服務時,它的服務率會線性增加。
對於這個佇列,
並且狀態轉移圖是
解簡化為
並且
現在
因此
結合得到
佇列中的平均數量為
或者令 r = k-1
平均響應時間 T 透過應用 Little 公式 找到,得到
或
這是預期的,因為沒有作業必須等待才能開始接收服務。
無限伺服器佇列通常用於對計算機系統建模,以表示使用者終端組或表示不涉及排隊或作業之間衝突的隨機延遲。
排隊網路是透過將一個佇列的輸出連線到另一個佇列的輸入來構建的。如下所示。
請注意,單個佇列可以從多個佇列的輸出中饋送,並且佇列的輸出可以被拆分為多個佇列的輸入流。每個佇列形成網路的“節點”,這些節點可以編號為 1、2…M,其中 M 是網路中的節點數。“路由機率”是從網路的節點 i 出發立即到達節點 j 的機率。
排隊網路可以用來模擬多個互動裝置的系統,每個裝置都可以被建模為一個佇列。例如,由 CPU 和磁碟組成的簡單計算機系統可以用一個 2 佇列網路來表示。
排隊網路可以是“開放”的或“封閉”的。在開放網路中,作業從外部源到達某些節點,並且可以從某些節點離開網路(到某個吸收目的地或“匯點”)。網路中的作業數量可以變化,並且源具有無限的供應。在封閉網路中,固定數量的作業在網路的節點之間迴圈;沒有新作業進入網路,也沒有作業離開網路。
封閉網路在對計算機系統建模方面特別成功。兩種最常用的模型是中央伺服器模型和機器維修員模型。
下面顯示了中央伺服器排隊網路。
這裡節點 1 表示 CPU,節點 2 到 M 表示系統輸入/輸出 (I/O) 裝置——通常是磁碟控制器。作業被視為在 CPU 上接收服務,然後以機率 路由到 I/O 裝置 i。在 I/O 裝置上接收服務後,作業返回到 CPU。在這個模型中,計算機系統對作業的處理由作業多次訪問 CPU 和 I/O 裝置來表示。從 CPU 返回自身的路徑(以機率 )代表系統中一個作業的完成和另一個作業的同步開始。
中央伺服器網路特別適用於對多道程式計算機系統的內部資源(CPU 和磁碟)進行建模。在這些系統中,為了提高系統效率,多道程式級別(記憶體中同時執行的作業數量)通常限制為少量作業。在中度到重度負載下,系統多道程式級別通常處於或接近此限制。因此,假設網路中的作業數量是恆定的,這很好地近似於實際系統。
機器維修員模型最初是在運籌學中開發的,通常用於表示互動式計算機系統。該網路,如下圖所示
有一個多伺服器節點,表示使用者終端。另一個(系統)節點表示其他系統資源。這些可以任意連線,儘管通常使用中央伺服器網路的變體。作業從終端節點開始,然後進入系統,在系統節點之間迴圈,然後返回到終端節點。從作業離開終端節點到它返回的時間是系統響應時間,它在終端節點花費的時間稱為使用者思考時間。網路中的作業數量與終端節點上的伺服器數量相同。因此,沒有作業等待開始在該佇列中接收服務,並且它的服務時間與思考時間相同。
開放網路最常用於對具有可變作業數量或恆定作業到達率的計算機系統進行建模。批處理系統和通訊網路通常是這種型別。
許多互動式計算機系統的一個特別有用的模型是下面所示的終端驅動的系統。
在這個模型中,作業的數量等於終端的數量(即每個終端有一個作業)。作業被視覺化為在使用者按下“回車鍵”時離開“終端”,在系統中經過各種裝置進行處理,然後返回到終端節點。從作業離開終端節點到返回的時間是系統響應時間。作業在終端等待的時間(即從響應到下一個系統輸入的時間)是使用者“思考時間”。
Let: denote the rate with which jobs enter the system (system throughput); R denote the system response time; Z denote the user think time; N denote the number of terminals (or jobs) in the System.
現在我們將 Little 公式應用於包含終端和系統(大寫 S)的 SYSTEM(所有大寫字母)。
對於 SYSTEM,每個作業在終端平均花費時間 Z,在系統中平均花費時間 R,在 SYSTEM 中平均花費時間 Z + R。然後它離開並立即返回。平均作業吞吐率為,系統中的作業數量固定為 N。
因此,根據 Little 公式
或
現在我們試圖找到響應時間 R 和吞吐率 的界限。
設系統中的各種裝置編號為 1,2,...M,設 是作業從裝置 i 接收的平均總服務量。注意,當作業在系統中時,它實際上可能多次訪問裝置 i,在這種情況下 是它在每次訪問時接收的服務量的總和。設 是作業在每次訪問裝置 i 時接收的平均服務量。如果 與 i 無關,那麼
是作業訪問裝置 i 的平均次數。
如果只有一個終端,因此係統中只有一個作業,R 僅僅是作業從每個裝置需要的服務量的總和。這是可能的最小響應時間。因此
由於每個裝置的利用率不能超過 100%,因此裝置 i 的吞吐率 充其量為 。因此,
並且由於作業在每次透過系統時平均訪問裝置 i 次,
因此,
將此公式代入響應時間表達式得到下界
為了找到 R 的上界,我們注意到作業在任何裝置 i 上花費的最長時間將發生在每次訪問時,它必須等待其他 N-l 個作業完成服務才能接收其服務。因此,
下面顯示了這些響應時間與系統中終端數量的關係。虛線顯示了典型的系統響應時間函式。
之間的區域通常被稱為系統的可行響應時間區域。在實踐中,隨著終端數量的增加,響應時間變得漸近於直線
這是 最左邊的線,也是 的最大值的線。對應於這條線的裝置被稱為系統瓶頸,其他裝置的其他線是由於這些裝置造成的潛在瓶頸。上面提到的瓶頸和潛在瓶頸很容易找到。觀察到每個都是一條直線,它在水平(終端)軸上的截距為 ,斜率為 。由於 隨著線從左到右移動而變小,它們看起來像是“落下”。
從 中,對於所有 i,我們注意到
其中 是最大 的裝置的總服務時間。這是系統可能的最大吞吐量。
重新排列得到 的表示式
我們注意到系統中存在 N 個作業。因此,
類似地,由於 ,我們有:
下圖顯示了這些系統吞吐量與終端數量關係的界限。
點
在前面兩張圖中顯示,被稱為系統的飽和點。它解釋如下。
當一個終端連線到系統時,作業永遠不會因為等待其他作業在裝置上接收服務而被延遲。因此,它在系統中花費時間 ,吞吐量為 。如果隨著終端數量的增加,每個進入系統的作業都沒有因為等待其他作業被服務而被延遲,那麼每個作業只會在系統中花費時間 。響應時間將為 ,吞吐量將沿線 增加。
然而,當終端數量 N 變得等於 N* 時,系統吞吐量將達到 ,瓶頸裝置將達到 100% 的利用率。此時它“飽和”。如果此時再新增一個作業進入系統,那麼作業只能在另一個作業開始服務時到達瓶頸裝置。因此,每個作業都必須等待一段時間才能開始自己的服務。因此,對於每個超過 N* 的終端,最小可能的響應時間增加 ,最小響應時間將沿線 增加。
前面兩張圖中的界限提供了關於我們開始修改系統配置時系統行為的見解。
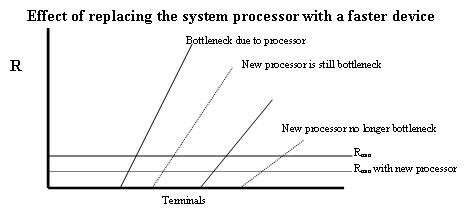
例如,考慮一個計算機系統,其中處理器處理終端 I/O 流量並且是系統瓶頸。設 是作業在處理器上接收的平均處理時間。如果處理器被更快的裝置替換,就會減少。因此延遲 會減少,並且由於處理器造成的“潛在瓶頸”向右移動。如果它移動足夠遠,以至於另一個裝置成為最左邊的潛在瓶頸,那麼該裝置就成為新的瓶頸。如果它沒有移動到其他潛在瓶頸的右邊,那麼它仍然是瓶頸,但是可以獲得更低的響應時間和更高的吞吐量。下圖顯示了這些更改對響應時間漸近線的影響。
如果將終端 I/O 處理解除安裝到前端處理器(FEP)上,則會出現更有趣的情況。這也減少了 並將處理器瓶頸向右移動,但它向系統添加了一個新裝置和相應的潛在瓶頸。
設 是處理器花費在 I/O 上的時間。那麼 將減少 。如果 FEP 比處理器慢,那麼 將大於 ,並且 將增加 - 。如果 FEP 更快, 將減少 。
如果系統負載很重,以至於處理器是控制響應時間並限制吞吐量的活動瓶頸;只要系統吞吐量將增加,即使 FEP 比處理器慢得多。當處理器瓶頸向右移動時,哪個裝置成為新的系統瓶頸取決於 和系統中的其他裝置的值。
飽和於
問題
Can we get 1 sec response time? – No. Can we get 2 sec response time with 30 terminals? – Yes. Can we get 2 sec response time with 35 terminals? – No.
CPU 是瓶頸。使用更快的 CPU 來獲得更好的效能。
更快的 CPU 導致更短的處理時間(比如 0.75 秒)。
導致效能大幅提升。
更快的磁碟…
…會稍微好一點,但效果不大。
稍微更快的 CPU, vcxc = 0.6 …
…CPU 仍然是瓶頸。
然而,如果 vcxc = 0.4 …
…那麼磁碟現在是瓶頸,CPU 的進一步改進幫助不大。
新增第二個 CPU…
邊界模型獨立於內部系統結構。該模型依賴於每個裝置上作業所需的總服務。因此,邊界模型可以表示為序列系統。
total service = vixi = Ti is easy to measure Ui is easy to measure is easy to measure vi is usually hard to measure xi is usually hard to measure