計算機系統工程/可靠性模型
系統是由多個元素組合在一起形成的整體。
- 河流或交通系統
- 貨幣系統
- 特定領域中的事實、原則和學說的綜合集合
- 標記、編號、測量等的系統
- 南卡羅來納大學 - 由哥倫比亞的主校區和許多分校組成
- 計算機(我們的主要興趣) - 包括元件:記憶體、處理器、主機板、磁碟、印表機、無線介面卡等。
並非每個集合都是一個系統。為了成為一個系統,一個集合需要具有一定的統一性,其元件之間具有功能關係,或者具有某種有用的目的。例如,房間裡的一組隨機物品,除非滿足上述條件之一,否則不會構成一個系統。
- 元件:用於輸入處理或輸出的操作部件
- 屬性:元件的特性,這些特性描述了系統
- 關係:元件和屬性之間的聯絡
元件是相互關聯的,並協同工作以實現某種目的、目標或功能。每個元件的特性和行為都會影響整個系統的特性。例如,計算機記憶體的速度、磁碟訪問時間和容量都會影響計算機的整體速度。每個元件的特性都依賴於至少一個其他元件。例如,記憶體效能取決於匯流排速度(頻寬)。每個元件的子集(或子系統)都以相同的方式相互關聯,但系統不能被分成獨立的子集。
通常,系統具有元件層次結構。一個系統由元件組成,而這些元件又由更小的元件組成。較低的層次結構稱為子系統。一個例子是硬碟驅動器。驅動器是計算機的一個元件,但它具有多個磁碟、讀寫頭、緩衝區以及許多其他更小的元件。
- 自然和人造(人造)
- 物理和概念
- 靜態和動態
- 封閉和開放
工程學關注的是為了造福人類而對有限資源的經濟利用。這是透過考慮以下幾個方面來解決問題的。在系統工程領域,必須定義與真實客戶需求相關的產品和系統需求。例如,設計滿足客戶通訊需求的電子郵件系統,必須很好地定義以滿足這些需求。工程學還必須解決整個系統,包括所有元素,並從生命週期角度出發。必須考慮整個層次結構,包括各個層次之間的互動以及同一層次上的各個元素之間的互動。計算機系統中這方面的示例是記憶體層次結構,由二級快取、主記憶體和硬碟上的虛擬記憶體組成。通常需要將各種相關學科在一個及時且同步的方式中組織成一項工程工作,例如系統的機械和電氣方面的不同方面。最後,建立對過程的規範化方法(管理過程以獲得結果)至關重要。這包括適當的審查、評估和反饋,以確保有序和高效的進展。
以下是對該過程應用示例:第三世界國家的獨裁者通常想乘坐豪華汽車。然而,這種喜好並不得到太多支援。加油站並不普遍,經濟可能無法支援許多接受過汽車維修培訓的技工。因此,從工程學的角度來看,這個系統將需要更多的設計和資金才能變得可行。
- 自頂向下:將系統作為一個整體來看
- 以生命週期為導向
1. Design, development production/construction, distribution, operation, maintenance & support, retirement, phaseout, disposal 2. Past emphasis on design & acquisition, with little emphasis on production, operation, maintenance, support & disposal 3. Example: If an old computer goes to a landfill (taking up space and polluting the groundwater), a better design would allow the recovery of gold, lead, and other materials upon disposal.
- 更好地定義系統需求 - 將客戶需求追溯到各個元件
- 跨學科
1. Systems usually require multiple disciplines 2. Example: In the development of a computer game, a company has 3 employees – an artist, a musician, & a programmer.
“Reliability is the probability of a device performing adequately for the period of time intended under the operating conditions encountered.” – NASA
Reliability, R(t), is the probability of a system not failing during the period [0,t].
測試大量系統。
危險函式,h(t)
分離變數並積分
摘要 F(t) 是失效分佈函式 R(t) = 1-F(t) 是可靠性 f(t) 是失效密度函式 h(t) 是危險函式
f(t) 和 h(t) 的區別
在 2 到 3 時刻
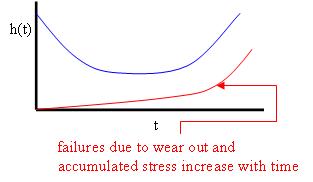
危險函式的形狀表明了物品如何老化。它有一個直觀的解釋,即物品在時刻 t 所承受的風險量
遞增危險函式 這可能是最可能的情況,因為物品會隨著時間的推移而磨損或退化。例如,看看會經歷磨損或疲勞的機械物品,例如隨著時間的推移,汽車輪胎上的橡膠會變薄。
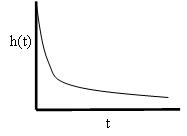
遞減危險函式 在這種情況下,物品會得到改善;也就是說,物品隨著時間的推移不太可能失效。例如,一些金屬透過持續使用而“硬化”。此外,隨著錯誤的修復,軟體可能會得到改善。
浴缸型失效率 這種情況描述了許多自然系統和製成品。它是三種效應的綜合
*early failures due to defects *late failures due to wear out *accidents at a constant rate
人類生命特徵
MTTF = 800 年對應於失效率
或 1 年內 4000 人中 5 人死亡
回顧
這種分佈是最常用的可靠性模型。它對許多電子元件在其大部分壽命中有效,並且是 MIL-HDBK-217 的基礎。
令 T = 物品壽命(隨機變數)
這是物品在存活到時刻 s 後失效分佈的條件機率,與全新的物品相同。
一個例子是保險絲。保險絲因電源浪湧而失效,但不會隨著時間的推移而減弱或退化。無記憶特性及其“用後如新”的假設在適用性上受到限制。為了簡單起見,指數分佈很容易被誤用
*statistical techniques are particularly tractable *can add failure rates *field data often allow an estimation of only this one-parameter distribution
C 提供了對資料集進行指數性快速檢查
瑞典物理學家沃洛迪·威布林在 1939 年引入了這種分佈。它是指數分佈的推廣,適用於對具有恆定、嚴格遞增和嚴格遞減危險函式的壽命進行建模。
請注意,威布林分佈可以匹配浴缸曲線的不同階段。
程式: 1. 收集失效資料。2. 將資料對威布林分佈進行最佳擬合
如果物品仍在磨合期
*Improve supplier quality *Burn in the system longer *Be more careful while manufacturing
在通用電氣,燈泡的燈絲即使只有 1% 的差異也會導致壽命縮短 25%。
如果歸因於隨機失效(事故)
*Make stronger components *Derate – use components at less than the rated value *Use newer technology (i.e. software control, longer-life transistors instead of vacuum tubes, etc.) *Make components less environmentally sensitive (i.e. better packaging) *NPN transistors < PNP transistors
例如,鹵素燈和緊湊型熒光燈使用不同的技術來延長壽命。此外,白熾長壽命燈泡的額定功率可能如下進行
如果物品處於磨損區域
*Use stronger, longer-lived components *Use newer technology, etc. *Use a different architecture
平均故障間隔時間 (MTTF) 這意味著只有大約 37% 的物品在超過 1 個 MTTF 後存活。但是,這種分佈有一個非常長的尾部
平均維修時間 (MTTR)
平均故障間隔時間 (MTBF)
請注意,MTBF 和 MTTF 通常被一些作者幾乎互換使用。
例如,如果一個系統在兩年內只有 15 分鐘的停機時間,那麼
對於串聯絡統
如果 A 工作且 B 工作且 C 工作且 D 工作,則系統工作。
例如,如果
在時間方面,
假設
觀察到,對於恆定失效率(指數)模型,可以使用威布林分佈
但這要困難得多。
- 非常簡單
- 非常有吸引力
- 非常具有欺騙性
元件可靠性 = 0.9
如果任何一個元件工作,系統就工作,如果兩個元件都失效,系統就失效。R = 1-P(fail)
= 1-P(first fails & second fails) = 1-P(first fails)P(second fails) = 1-P(.1)(.1) note independence = .99
示例:燈泡
串聯絡統
並聯系統
- 為了提高可靠性、可用性
- 消除單點故障
Important in military systems Becoming important in commercial systems Important in high availability systems in which the part being repaired must be shut down
- 可降級容錯
另一個例子
系統失效的機率 = (A 失效的機率)AND (B 失效的機率)
觀察到這不是指數的。
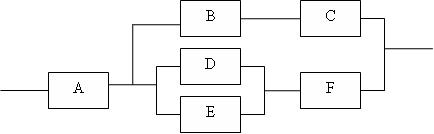
組合串聯或並聯元件可靠性以獲得等效可靠性,並簡化系統。請參閱以下示例
1) 簡化 D、E
2) 簡化 B、C 和 I、F
3) 簡化 II、III
檢查以下具有相同元件的 4 元件系統的兩種不同配置。元件失效率為
結論:透過在儘可能低的級別上使系統冗餘,我們可以在可靠性方面獲得最大的收益。通常,使模組冗餘比複製系統更好。
使模組冗餘以實現可靠性目標。
示例:調幅訊號拾取
串聯絡統
冗餘設計 I 元件級串聯-並聯
如果一個元件失效,功能引數可能會發生變化 - 很可能。
冗餘設計 II 並聯串聯
組合輸出
並聯子系統之間的介面增加了設計複雜性(從而降低了可靠性)。
元件計數可靠性模型假設系統是串聯的;這種模型低估了冗餘系統的可靠性。對於冗餘系統,元件計數模型用於估計串聯子系統和介面的可靠性。然後在考慮冗餘結構的同時計算可靠性。
再次使用我們的調幅訊號拾取示例
地面移動環境 (GM)
串聯子系統
介面
系統可靠性估計
單工系統
簡單冗餘系統(忽略介面問題)
R = 0.9876
注意: 在某些情況下,介面可靠性可能主導冗餘子系統可靠性,並決定整體系統可靠性。在這種情況下,單一系統可能比冗餘系統更可靠。
使用分解
- 找到關鍵元件,並根據關鍵元件是否良好將系統進行分割槽。
- 關鍵元件將系統的可靠性結構繫結在一起。
全機率定律
示例
選擇 A 作為關鍵元件。
如果 A 良好
串聯/並聯系統
如果 A 不好
串聯絡統
便捷符號
注意
- 如果選擇“錯誤”的關鍵元件,元件分解技術有效,但簡化程度不那麼大。
- 可以重複選擇新的關鍵元件以進一步簡化子系統。
只要 1 個模組工作,該系統就能正常工作。
M-out-of-N 系統可靠性
如果至少有 M 個模組工作,該系統就能正常工作。
它最多可以容忍 N-M 個故障,因此
投票器比較所有 N 個模組的輸出並輸出多數結果。這被稱為 N 模冗餘 (NMR)。NMR 系統通常具有奇數個模組,因此 。如果 (n+1) 個模組工作(最多可以有 n 個故障),並且投票器工作,則系統就能正常工作。
簡單投票器
模擬訊號或數字投票
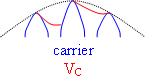
投票器比較輸入訊號(或數字值),並選擇中間值作為其輸出。正常操作如下
但是,可能會出現錯誤情況
注意: 可靠性計算假定最壞情況
- 所有模組都以相同的邏輯方向發生故障
- 沒有補償故障(即,一個模組卡在 1,而另一個卡在 0)
示例
NMR 系統可靠性比較
以 MTTF 為單位度量時間。
下圖描述了 NMR 系統在 N 增加時的可靠性
觀察
額外的硬體在短期內提高了可靠性,但一旦冗餘用完,就只有更多的硬體會發生故障,可靠性就會迅速下降。
對於 TMR 系統
對於冗餘系統,MTTF 可能不是可靠性的合適度量標準。需要根據任務時間檢視 R(t)。
投票器提供一個簡單的故障點,因此設計可能可以將投票器複製三次 (TMR)。
系統可靠性由第一階段的 3 個並聯模組、最後一階段的投票器以及中間階段的並聯投票器-模組決定。
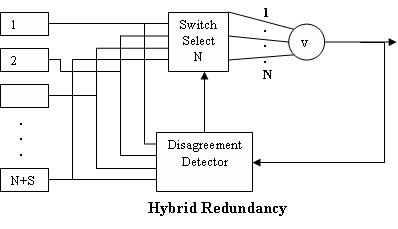
在 NMR 系統中,故障模組會不斷累積,直到它們成為多數,系統發生故障。可以透過清除所有故障模組來延長系統壽命。這可以透過混合冗餘(使用備件)或自適應投票(也稱為更改投票)來實現。本質上,必須首先檢測到故障模組。
該系統具有以下屬性
- N+S 個模組(S 個備件)
- 差異檢測器將投票輸出與模組輸出進行比較
- 開關選擇來自 N 個模組的輸出以提供給投票器
- 如果模組發生故障,差異檢測器會告訴開關用備用模組替換故障模組
這種配置通常與 TMR 系統一起使用。如果切換了太多備件,其複雜性會增加到其可靠性主導系統可靠性的程度。
假設我們有 3 個程式設計師編寫程式碼,然後對結果進行投票。在 TMR 系統中,每個程式都可以在完全不同的硬體集上執行。但是,軟體的勞動強度大,生產成本非常高。N 超程式設計會大幅增加此成本,無法保護免受規範錯誤,並且會引入時間和協調問題,因為每個程式都不相同。
在自適應投票中,將投票輸出與模組輸出進行比較。當模組發生故障時,它將與另一個模組一起被移除(這樣做是為了保持奇數個模組)。然後,投票器將更改為選擇剩餘模組中的多數。這種方法可以與混合冗餘結合使用,以將良好的模組切換回系統。投票(特別是 TMR)在許多容錯、超高可靠性計算機系統中使用。
- 使用 A 操作
- A 發生故障時切換到 B
- A 和 B 不 獨立
一般而言,A 和 B 可以不同(例如,A 可以是線上電源,而 B 可以是發電機)。需要注意的是,B 在備用模式下也可能發生故障,或者開關也可能發生故障。檢查以下簡單情況。假設
可靠性如下
回想一下,以上是全機率定律。
因此,
每次裝置發生故障並切換到新的裝置時,故障序列都會形成一個從頭開始的過程。這被稱為更新過程。兩次故障之間的時間服從指數分佈,其中 X 是表示兩次故障之間時間的隨機變數。假設我們有 n 個系統,如下所示
回想一下,對於泊松過程,i) 非重疊區間的事件是獨立的 ii) P(小區間 h 中有事件) = P(h 中沒有事件) = iii) 兩次事件之間的時間 X 服從指數分佈,iv) 區間 T 中的事件數量 n(T) 服從泊松分佈。
還要回憶一下(對於 iii)
此外,
正如您可能已經推斷的那樣,這個故障序列是一個泊松過程。因此,
對於 n 個元件系統
作為概述,比較以下兩個單元的比較
- 備用冗餘
- 並聯冗餘
- 單工系統
- 備用冗餘
- 並聯冗餘
- 單一系統:R = p