資料編碼理論/霍夫曼編碼

從文字 "this is an example of a huffman tree" 中生成的確切頻率生成的霍夫曼樹。每個字元的頻率和程式碼如下所示。使用此程式碼對句子進行編碼需要 135 位，不包括樹的空間。

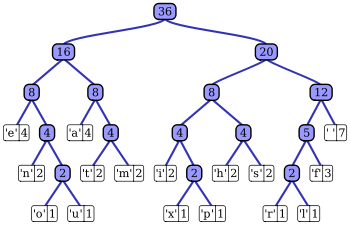
字元	頻率	程式碼
空格	7	111
a	4	010
e	4	000
f	3	1101
h	2	1010
i	2	1000
m	2	0111
n	2	0010
s	2	1011
t	2	0110
l	1	11001
o	1	00110
p	1	10011
r	1	11000
u	1	00111
x	1	10010

在計算機科學和資訊理論中，霍夫曼編碼是一種用於無損資料壓縮的熵編碼演算法。該術語指的是使用變長碼錶來編碼源符號（例如檔案中的字元），其中變長碼錶是根據源符號每個可能值的估計出現機率以特定方式推匯出來的。它是由 David A. Huffman 在麻省理工學院攻讀博士學位期間開發的，並於 1952 年發表在論文 "A Method for the Construction of Minimum-Redundancy Codes" 中。

霍夫曼編碼使用一種特定方法來選擇每個符號的表示，從而產生一個字首碼（有時稱為“字首自由碼”）（即，表示某個特定符號的位元串永遠不會是表示任何其他符號的位元串的字首），該字首碼使用比用於不太常見的源符號的更短的位元串來表達最常見的字元。霍夫曼能夠設計出此型別最有效的壓縮方法：當實際符號頻率與用於建立程式碼的頻率一致時，將單個源符號對映到唯一的位元串的其他對映不會產生更小的平均輸出大小。後來發現了一種方法可以在輸入機率（也稱為權重）排序的情況下以線性時間完成此操作。

對於一組具有均勻機率分佈且成員數量為 2 的冪的符號，霍夫曼編碼等同於簡單的二進位制塊編碼，例如 ASCII 編碼。霍夫曼編碼是一種建立字首碼的非常普遍的方法，以至於術語“霍夫曼碼”被廣泛用作“字首碼”的同義詞，即使這樣的碼不是由霍夫曼演算法生成的。

雖然霍夫曼編碼對於已知輸入機率分佈的符號按符號編碼（即不相關符號流）是最佳的，但其最優性有時會意外地被誇大。例如，算術編碼和 LZW 編碼通常具有更好的壓縮能力。這兩種方法都可以組合任意數量的符號以實現更有效的編碼，並且通常適應實際的輸入統計資料，後者在輸入機率未知或在流中變化很大時很有用。一般來說，改進來自於輸入符號相關（cat 比 cta 更常見）。

歷史

1951 年，David A. Huffman 和他的麻省理工學院資訊理論同學可以選擇一篇學期論文或期末考試。教授 Robert M. Fano 指派了一篇關於尋找最有效二進位制碼的論文。霍夫曼無法證明任何程式碼是最有效的，正要放棄開始準備期末考試時，他突然想到使用頻率排序的二叉樹，並很快證明了這種方法是最有效的。

這樣做，這位學生超過了他的教授，他的教授曾與資訊理論發明家克勞德·夏農合作開發了一種類似的程式碼。霍夫曼透過自下而上而不是自上而下構建樹，避免了次優夏農-法諾編碼的重大缺陷。

問題定義

非正式描述

給定

一組符號及其權重（通常與機率成正比）。

查詢

具有最小預期碼字長度的字首自由二進位制碼（一組碼字）（等效地，具有最小加權路徑長度的樹）。

形式化描述

輸入.
字母表 $A=\left\{a_{1},a_{2},\cdots ,a_{n}\right\}$，它是大小為 $n$ 的符號字母表。
集合 $W=\left\{w_{1},w_{2},\cdots ,w_{n}\right\}$，它是（正）符號權重（通常與機率成正比）的集合，即 $w_{i}=\mathrm {weight} \left(a_{i}\right),1\leq i\leq n$。

輸出.
程式碼 $C\left(A,W\right)=\left\{c_{1},c_{2},\cdots ,c_{n}\right\}$，它是一組（二進位制）碼字，其中 $c_{i}$ 是 $a_{i},1\leq i\leq n$ 的碼字。

目標.
令 $L\left(C\right)=\sum _{i=1}^{n}{w_{i}\times \mathrm {length} \left(c_{i}\right)}$ 為程式碼 $C$ 的加權路徑長度。條件：對於任何程式碼 $T\left(A,W\right)$，$L\left(C\right)\leq L\left(T\right)$。

樣本

輸入 (A, W)	符號 (ai)	a	b	c	d	e	總和
	權重 (wi)	0.10	0.15	0.30	0.16	0.29	= 1
輸出 C	碼字 (ci)	000	001	10	01	11
	碼字長度（以位元為單位） (li)	3	3	2	2	2
	加權路徑長度 (li wi )	0.30	0.45	0.60	0.32	0.58	L(C) = 2.25
最優性	機率預算 (2-li)	1/8	1/8	1/4	1/4	1/4	= 1.00
	資訊量（以位元為單位） (−log2 wi) ≈	3.32	2.74	1.74	2.64	1.79
	熵 (−wi log2 wi)	0.332	0.411	0.521	0.423	0.518	H(A) = 2.205

對於任何雙唯一的程式碼，這意味著程式碼是可唯一解碼的，所有符號的機率預算之和總是小於或等於 1。在這個例子中，總和嚴格等於 1；因此，程式碼被稱為完整程式碼。如果情況並非如此，則始終可以透過新增額外的符號（以及相關的零機率）來推匯出等效程式碼，從而使程式碼完整，同時保持其雙唯一性。

如夏農（1948）所定義，每個符號 a_i 的資訊量 h（以位元為單位）具有非零機率，為

$h(a_{i})=\log _{2}{1 \over w_{i}}.$

熵 H（以位元為單位）是在所有具有非零機率 w_i 的符號 a_i 上，每個符號的資訊量的加權和

$H(A)=\sum _{w_{i}>0}w_{i}h(a_{i})=\sum _{w_{i}>0}w_{i}\log _{2}{1 \over w_{i}}=-\sum _{w_{i}>0}w_{i}\log _{2}{w_{i}}.$

(注意：機率為零的符號對熵沒有貢獻。當 w = 0 時，$w\log _{2}(1/w)=0\cdot \infty$ 是一個不定式；因此，根據洛必達法則

$\lim _{w\to 0^{+}}{\frac {\log _{2}{\frac {1}{w}}}{\frac {1}{w}}}=\lim _{w\to 0^{+}}{\frac {-{\frac {1}{w\ln 2}}}{-{\frac {1}{w^{2}}}}}=\lim _{w\to 0^{+}}{\frac {w}{\ln 2}}=0$.

為了簡單起見，上述公式中省略了機率為零的符號。

根據夏農資訊理論的信源編碼定理，資訊熵是給定字母表及其權重下，理論上可能的最小碼字長度的度量。在這個例子中，加權平均碼字長度為每個符號 2.25 位元，僅略大於計算出的每個符號 2.205 位元的資訊熵。因此，此程式碼不僅在沒有其他可行程式碼效能更好的意義上是最優的，而且它也非常接近夏農確定的理論極限。

注意，一般來說，霍夫曼編碼不一定是唯一的，但它始終是最小化 $L(C)$ 的程式碼之一。

基本技術

信源生成 4 個不同的符號 $\{a_{1},a_{2},a_{3},a_{4}\}$，其機率為 $\{0.4;0.35;0.2;0.05\}$。從左到右生成二叉樹，取兩個機率最小的符號，將它們合併在一起形成另一個等效符號，其機率等於兩個符號的機率之和。重複此過程，直到只剩下一個符號。然後可以從右到左反向讀取樹，為不同的分支分配不同的位。最終的霍夫曼編碼為

符號	程式碼
a1	0
a2	10
a3	110
111

用 2 位/符號來表示由 4 個符號組成的訊號的標準方法，但信源的資訊熵為 1.73 位/符號。如果使用此霍夫曼編碼來表示訊號，則平均長度將降低到 1.85 位/符號；它仍然遠低於理論極限，因為符號的機率不同於 2 的負冪。

該技術透過建立節點的二叉樹來實現。這些可以儲存在常規陣列中，陣列的大小取決於符號的數量 $n$。節點可以是葉節點或內部節點。最初，所有節點都是葉節點，它們包含符號本身、權重（出現頻率）和可選的指向父節點的連結，這使得從葉節點開始很容易反向讀取程式碼。內部節點包含符號權重、指向兩個子節點的連結和可選的指向父節點的連結。根據慣例，位 '0' 表示跟隨左子節點，位 '1' 表示跟隨右子節點。一個完整的樹有 $n$ 個葉節點和 $n-1$ 個內部節點。

該過程基本上從葉節點開始，葉節點包含它們代表的符號的機率，然後建立一個新節點，其子節點是 2 個機率最小的節點，這樣新節點的機率就等於子節點的機率之和。將之前的 2 個節點合併為一個節點（因此不再考慮它們），並考慮新節點，重複此過程，直到只剩下一個節點，即霍夫曼樹。

最簡單的構造演算法使用優先佇列，其中機率最低的節點具有最高優先順序。

1. 為每個符號建立一個葉節點，並將其新增到優先佇列中。
2. 當佇列中有多個節點時
   1. 從佇列中移除兩個優先順序最高（機率最低）的節點。
   2. 建立一個新的內部節點，將這兩個節點作為子節點，並將機率設定為兩個節點的機率之和。
   3. 將新節點新增到佇列中。
3. 剩餘的節點是根節點，樹已經完成。

由於高效的優先佇列資料結構每次插入需要 O(log n) 時間，並且具有 n 個葉節點的樹有 2n−1 個節點，因此該演算法在 O(n log n) 時間內執行。

如果符號按機率排序，則可以使用兩個佇列建立線性時間 (O(n)) 的霍夫曼樹，第一個佇列包含初始權重（以及指向相關葉節點的指標），組合權重（以及指向樹的指標）被放入第二個佇列的尾部。這確保了最低權重始終保留在兩個佇列的頭部之一。

1. 從與符號數量相同的葉節點開始。
2. 將所有葉節點入隊到第一個佇列中（按機率升序，以便機率最低的項位於佇列頭部）。
3. 當佇列中有多個節點時
   1. 透過檢查兩個佇列的頭部，將兩個權重最低的節點出隊。
   2. 建立一個新的內部節點，將這兩個剛剛移除的節點作為子節點（任何節點都可以是任何子節點），並將它們的權重之和作為新權重。
   3. 將新節點入隊到第二個佇列的尾部。
4. 剩餘的節點是根節點；樹現在已經生成。

最小化碼字長度的方差通常是有益的。例如，接收霍夫曼編碼資料的通訊緩衝區可能需要更大才能處理特別長的符號，如果樹特別不平衡的話。為了最小化方差，只需透過選擇第一個佇列中的項來打破佇列之間的聯絡。這種修改將保留霍夫曼編碼的數學最優性，同時最小化方差和最長字元程式碼的長度。

主要屬性

使用的機率可以是基於平均經驗的應用程式域的通用機率，也可以是壓縮文字中實際發現的頻率。（這種變化要求將頻率表或其他編碼提示儲存在壓縮文字中；實現採用各種技巧來有效地儲存表。）

當每個輸入符號的機率都是 2 的負冪時，霍夫曼編碼是最優的。字首碼在較小的字母表上往往效率略低，在這種情況下，機率通常落在這些最佳點之間。“阻塞”，或透過將多個符號合併成固定長度或可變長度的“詞”來擴充套件字母表大小，然後進行霍夫曼編碼，通常會有所幫助，尤其是在相鄰符號相關聯的情況下（如自然語言文字）。霍夫曼編碼的最壞情況可能發生在符號的機率超過 2^-1 = 0.5 時，這使得效率的上限無界。這些情況通常對稱為遊程長度編碼的阻塞形式有很好的反應。

算術編碼比霍夫曼編碼略有優勢，但在實踐中，這些優勢很少大到足以抵消算術編碼更高的計算複雜度和專利使用費。（截至 2006 年 7 月，IBM 在美國擁有許多算術編碼方法的專利；請參閱關於算術編碼的美國專利。）

變化

哈夫曼編碼有很多變體，其中一些使用類似哈夫曼的演算法，而另一些則找到最佳字首碼（例如，對輸出施加不同的限制）。請注意，在後一種情況下，該方法不必類似哈夫曼，實際上也不必是多項式時間。一篇關於哈夫曼編碼及其變體的論文列表，見“無損源編碼的程式碼和解析樹”[1].

n元哈夫曼編碼

n元哈夫曼演算法使用{0, 1, ... , n − 1}字母表來編碼訊息並構建一個n元樹。這種方法在哈夫曼最初的論文中有所考慮。與二進位制（n等於2）程式碼相同，只是n個機率最小的符號被組合在一起，而不是僅僅組合2個機率最小的符號。請注意，對於大於2的n，並非所有源詞集都可以正確地為哈夫曼編碼形成一個n元樹。在這種情況下，必須新增額外的0機率佔位符。這是因為樹必須形成一個n到1的壓縮器。對於二進位制編碼，這是一個2到1的壓縮器：任何大小的集合都可以形成這樣的壓縮器。

自適應哈夫曼編碼

一種稱為自適應哈夫曼編碼的變體根據源字串中最近的實際頻率動態計算機率。這與LZ演算法家族有些相關。

哈夫曼模板演算法

在哈夫曼編碼的實現中，權重通常表示數值機率，但是上面給出的演算法並不需要這個；它只需要一種對權重進行排序和加和的方法。哈夫曼模板演算法允許使用任何型別的權重（成本、頻率、權重對、非數值權重）以及許多組合方法之一（不僅僅是加法）。這樣的演算法可以解決其他最小化問題，例如最小化 $\max _{i}\left[w_{i}+\mathrm {length} \left(c_{i}\right)\right]$，這個問題最初應用於電路設計[2].

長度限制哈夫曼編碼

長度限制哈夫曼編碼是一種變體，其目標仍然是實現最小加權路徑長度，但有一個額外的限制，即每個碼字的長度必須小於給定的常數。包合併演算法使用一種簡單的貪婪方法解決這個問題，該方法與哈夫曼演算法非常相似。其時間複雜度為 $O(nL)$，其中 $L$ 是碼字的最大長度。與預排序和未排序的常規哈夫曼問題分別不同，沒有已知的演算法能夠線上性或線性對數時間內解決這個問題。

不等字母成本的哈夫曼編碼

在標準的哈夫曼編碼問題中，假設構造碼字的集合中的每個符號都有相同的傳輸成本：一個長度為N位的碼字始終具有N的成本，無論其中有多少位是0，有多少位是1等等。在假設下，最小化訊息的總成本和最小化數字的總數是相同的。

不等字母成本的哈夫曼編碼是對這種假設不再成立的推廣：由於傳輸介質的特性，編碼字母的字母可能具有不均勻的長度。例如，莫爾斯碼的編碼字母表，其中一個“短劃線”的傳送時間比一個“點”更長，因此在傳輸時間中一個“短劃線”的成本更高。目標仍然是最小化加權平均碼字長度，但是僅最小化訊息使用的符號數量已經不足夠。沒有已知的演算法能夠以與常規哈夫曼編碼相同的方式或以相同效率解決這個問題。

最優字母二叉樹（Hu-Tucker編碼）

在標準的哈夫曼編碼問題中，假設任何碼字都可以對應於任何輸入符號。在字母版本中，輸入和輸出的字母順序必須相同。因此，例如，$A=\left\{a,b,c\right\}$ 不能分配程式碼 $H\left(A,C\right)=\left\{00,1,01\right\}$，而應該分配 $H\left(A,C\right)=\left\{00,01,1\right\}$ 或 $H\left(A,C\right)=\left\{0,10,11\right\}$。這也被稱為Hu-Tucker問題，以發表了第一個線性對數解的論文作者命名，該解為這個最優二元字母問題，與哈夫曼演算法有一些相似之處，但不是這個演算法的變體。這些最優字母二叉樹通常用作二叉搜尋樹。

規範哈夫曼碼

如果與字母順序輸入對應的權重按數字順序排列，則霍夫曼編碼具有與最佳字母編碼相同的長度，可以透過計算這些長度來找到最佳字母編碼，從而使 Hu-Tucker 編碼變得不必要。從數字上（重新）排序輸入產生的程式碼有時被稱為*規範霍夫曼程式碼*，並且由於編碼/解碼的簡便性，它通常是實踐中使用的程式碼。尋找這種程式碼的技術有時被稱為**霍夫曼-夏農-法諾編碼**，因為它與霍夫曼編碼一樣最優，但重量機率按字母順序排列，就像夏農-法諾編碼一樣。與該示例對應的霍夫曼-夏農-法諾程式碼是$\{000,001,01,10,11\}$，它與原始解具有相同的程式碼字長度，因此也是最優的。

應用

儘管算術編碼提供的壓縮效能優於霍夫曼編碼，但霍夫曼編碼由於其簡單性、高速以及不受專利限制而仍然被廣泛使用。

如今，霍夫曼編碼通常用作其他一些壓縮方法的“後端”。DEFLATE（PKZIP 的演算法）和多媒體編解碼器（如 JPEG 和 MP3）具有前端模型和量化，然後進行霍夫曼編碼。

參考資料

• 霍夫曼的原始文章：D.A. 霍夫曼，“一種構造最小冗餘碼的方法”，《無線電工程師學會學報》，1952 年 9 月，第 1098-1102 頁
• 背景故事：簡介：David A. Huffman，《科學美國人》，1991 年 9 月，第 54-58 頁
• Thomas H. Cormen、Charles E. Leiserson、Ronald L. Rivest 和 Clifford Stein。演算法導論，第二版。麻省理工學院出版社和麥格勞-希爾出版社，2001 年。 ISBN 0-262-03293-7。第 16.3 節，第 385-392 頁。

外部連結

• 用於解釋霍夫曼編碼過程的程式。
• N 叉霍夫曼模板演算法
• Sloane A098950 最大高度霍夫曼樹的最小 K 階序列
• 在圖靈機上計算霍夫曼編碼
• Mordecai J. Golin、Claire Kenyon、Neal E. Young“具有不等字母成本的霍夫曼編碼”（PDF），STOC 2002：785-791
• 霍夫曼編碼：CS2 課程作業 這是一個很好的霍夫曼編碼入門
• 關於生成霍夫曼樹的快速教程
• 指向霍夫曼編碼視覺化的指標
• C 語言中的霍夫曼編碼
• JavaScript 中的霍夫曼編碼
• 霍夫曼二進位制演算法小程式
• 霍夫曼解碼的實現方法
• Python 實現的描述