R 中的資料探勘演算法/分類/決策樹

介紹

任何基於決策樹的演算法的操作哲學都非常簡單。事實上，儘管在執行某些步驟的方式上存在著重要的差異，但這類演算法的任何一種都基於分治的策略。總的來說，這種哲學是基於將問題逐次劃分為多個維度較少的子問題，直到可以找到每個簡單問題的解決方案。基於這一原理，基於決策樹的分類器試圖找到將宇宙逐次細分為更多子群的方法（建立包含相應測試的節點），直到每個子群只包含一個類別，或者直到某一類別顯示出明顯的優勢，從而不再需要進一步細分，在這種情況下，將生成一個包含多數類別的葉子。顯然，分類只是按照沿著樹排列的連續測試所指示的路徑進行，直到找到一個包含要分配給新示例的類別的葉子。

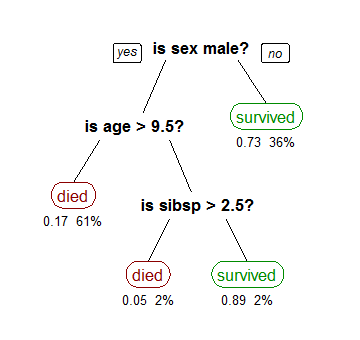
儘管所有基於決策樹的分類器都具有相同的基本哲學，但它們在構建方式上有很多種可能性。在選擇用於構建決策樹的演算法的所有關鍵點中，一些關鍵點應該因其重要性而突出顯示

用於選擇每個節點中使用的特徵的標準
如何計算示例集的劃分
何時決定某個節點是葉子
分配給每個葉子的類別的選擇標準是什麼

決策樹的一些重要優勢可以被指出，包括

可以應用於任何型別的資料
分類器的最終結構非常簡單，可以以一種優雅的方式儲存和處理
非常有效地處理條件資訊，將空間細分為獨立處理的子空間
通常顯示出健壯性，對訓練集中的錯誤分類不敏感
生成的樹通常易於理解，可以很容易地用於更好地理解所討論的現象。這可能是所有列出的優點中最重要的一點

演算法

決策樹的基本演算法是一種貪婪演算法，它以自上而下的遞迴分治方式構建決策樹。我們通常採用貪婪策略，因為它們效率高且易於實現，但它們通常會導致次優模型。也可以使用自下而上的方法。自上而下的決策樹演算法在演算法 1 中給出。它是一種遞迴分治演算法。它以資料集的子集 D 作為輸入，並評估所有可能的分割（第 4 到第 11 行）。選擇最佳分割決策（第 12 行），即資訊增益最高的分割，將資料劃分為兩個子集（分治），並遞迴呼叫該方法（第 14 和第 15 行）。當滿足停止條件時（第 1 到第 3 行），演算法停止。

停止條件

可以使用多種停止條件來停止遞迴過程。當任何一個條件為真時，演算法停止

所有樣本都屬於同一個類別，即具有相同的標籤，因為樣本已經是“純淨”的
如果大部分點已經屬於同一個類別，則停止。這是第一種方法的泛化，具有某些誤差閾值
沒有剩餘的屬性可以進一步分割樣本
分支測試屬性沒有樣本

屬性選擇

現在我們需要一個客觀的標準來判斷分割的質量。資訊增益度量用於在樹中的每個節點選擇測試屬性。具有最高資訊增益（或最大熵減少）的屬性被選為當前節點的測試屬性。該屬性將對結果分割槽中樣本進行分類所需的資訊降至最低。

總的來說，熵衡量系統中的無序程度或不確定性。在分類設定中，較高的熵（即更多的無序）對應於樣本具有混合標籤集合的情況。較低的熵對應於我們主要具有純分割槽的情況。在資訊理論中，樣本 D 的熵定義如下

H(D)=-\sum _{i=1}^{k}P(c_{i}|D)\log _{2}{P(c_{i}|D)}

其中 $P(ci|D)$ 是 D 中資料點被標記為類別 $c_{i}$ 的機率，k 是類別的數量。 $P(ci|D)$ 可以直接從資料中估計如下

P(c_{i}|D)={\tfrac {|\{x_{j}\in D|x_{j}{\text{ has label }}y_{j}=c_{i}\}|}{|D|}}

我們也可以將決策/分割的加權熵定義如下

H(D_{L},D_{R})={\tfrac {|D_{L}|}{|D|}}H(D_{L})+{\tfrac {|D_{R}|}{|D|}}H(D_{R})

其中D由於某種分割決策，被劃分為 $D_{L}$ 和 $D_{R}$ 。最後，我們可以將給定分割的資訊增益定義為

Gain(D,D_{L},D_{R})=H(D)-H(D_{L},D_{R})

換句話說，Gain是知道一個屬性的值後，熵的預期減少量。

Rpart

R 工具中找到的 rpart 包可用於決策樹分類，也可用於生成迴歸樹。遞迴劃分是資料探勘中的一項基本工具。它幫助我們探索資料集的結構，同時開發易於視覺化的決策規則，以預測分類（分類樹）或連續（迴歸樹）結果。rpart 程式使用兩階段程式構建具有非常通用結構的分類或迴歸模型；生成的模型可以表示為二叉樹。樹構建過程如下：首先找到最能將資料分成兩組的單個變數（“最佳”將在後面定義）。分離資料，然後將此過程分別應用於每個子組，遞迴地進行下去，直到子組達到最小尺寸（此資料為 5）或無法再進行改進為止。所得模型無疑過於複雜，因此像所有逐步程式一樣，問題就變成了何時停止。該過程的第二階段包括使用交叉驗證來修剪完整的樹。

生長樹

要生長一棵樹，請使用

    rpart (formula, data=, method=, control=)

其中

公式	格式為：outcome ~ predictor1+predictor2+predictor3+ect。
資料=	指定資料框
方法=	“class” 表示分類樹 “anova” 表示迴歸樹
控制=	用於控制樹生長的可選引數。例如，control=rpart.control(minsplit=30, cp=0.001) 要求節點中的最小觀測數為 30 才能嘗試分割，並且分割必須將總體擬合不足減少 0.001 倍（成本複雜度因子）才能嘗試。

視覺化和示例

printcp

printcp 命令顯示擬合 rpart 物件的 cp 表。根據複雜度引數列印最佳修剪的表。

用法

    printcp(object, digits=getOption("digits") - 2)

其中 object 是一個 rpart 物件，digits 是要列印的數字的位數。

示例

    fit <- rpart(Price ~ HP, car.test.frame)
    printcp(fit)

輸出

    Regression tree:
    rpart(formula = Price ~ HP, data = car.test.frame)
    Variables actually used in tree construction:
    [1] HP
    Root node error: 983551497/60 = 16392525
    n= 60
    CP nsplit rel error xerror xstd
    1 0.41417 0 1.00000 1.03808 0.21528
    2 0.12304 1 0.58583 0.71817 0.15575
    3 0.01000 2 0.46279 0.62650 0.11675

plotcp

plotcp 命令對 rpart 物件中的交叉驗證結果進行視覺化表示。一組來自巢狀集的樹的可能的成本複雜度修剪。對於 cp 值的間隔的幾何平均值（其中修剪是最佳的），通常在初始構建中已由 rpart 進行交叉驗證。擬閤中的 cptable 包含交叉驗證預測相對於每個幾何平均值的誤差的均值和標準差，並且這些誤差由該函式繪製。修剪的良好 cp 選擇通常是均值位於水平線以下的最左側值。

用法

    plotcp(object, minline = TRUE, lty = 3, col = 1, upper = c("size", "splits", "none"), args)

其中 object 是一個 rpart 物件，minline 指示是否在曲線的最小值之上繪製一條水平線，lty 是這條線的線型，col 是這條線的顏色，upper 指示在上軸上繪製的內容：樹的大小（葉子數）、分割數還是什麼都沒有，args 是要傳遞到或從其他方法傳遞的引數。

示例

    fit <- rpart(Kyphosis ~ Age + Number + Start, method="class", data=kyphosis)
    plotcp(fit)

檔案：First plot.png

rsq.rpart

將近似 r 平方與分割數以及不同分割的相對誤差與分割數繪製在一起（兩個圖）。

用法

    rsq.rpart(object)

其中 object 是一個 rpart 物件。

示例

    fit <- rpart(Mileage ~ Weight, car.test.frame)
    rsq.rpart(fit)

檔案：Second plot.png

列印

列印一個 rpart 物件。

用法

    print(object, minlength=0, spaces=2, cp, digits= getOption("digits"), args)

其中 object 是一個 rpart 物件，minlength 控制標籤的縮寫，spaces 是縮排增加深度的節點的空格數，digits 是要列印的數字的位數，cp 從列印輸出中修剪所有複雜度小於 cp 的節點，args 是要傳遞到或從其他方法傳遞的引數。

示例

    fit <- rpart(Kyphosis ~ Age + Number + Start, method="class", data=kyphosis)
    print(fit)

    n= 81
    node), split, n, loss, yval, (yprob)
    * denotes terminal node
    1) root 81 17 absent (0.7901235 0.2098765)
    2) Start>=8.5 62 6 absent (0.9032258 0.0967742)
    4) Start>=14.5 29 0 absent (1.0000000 0.0000000) *
    5) Start< 14.5 33 6 absent (0.8181818 0.1818182)
    10) Age< 55 12 0 absent (1.0000000 0.0000000) *
    11) Age>=55 21 6 absent (0.7142857 0.2857143)
    22) Age>=111 14 2 absent (0.8571429 0.1428571) *
    23) Age< 111 7 3 present (0.4285714 0.5714286) *
    3) Start< 8.5 19 8 present (0.4210526 0.5789474) *

總結

返回擬合的 rpart 物件的詳細列表。

用法

    summary(object, cp=0, digits=getOption("digits"), file, args)

其中 object 是一個 rpart 物件，digits 是結果中使用的有效數字位數，cp 修剪複雜度小於 cp 的節點，file 將輸出寫入給定檔名，args 是要傳遞給或從其他方法傳遞的引數。

示例

    fit <- rpart(Mileage ~ Weight, car.test.frame)
    summary(fit)

    Call:
    rpart(formula = Mileage ~ Weight, data = car.test.frame)
    n= 60
    CP nsplit rel error xerror xstd
    1 0.59534912 0 1.0000000 1.0294527 0.17907324
    2 0.13452819 1 0.4046509 0.6261647 0.10545991
    3 0.01282843 2 0.2701227 0.4746041 0.08567822
    4 0.01000000 3 0.2572943 0.4884699 0.08551818
    Node number 1: 60 observations, complexity param=0.5953491
    mean=24.58333, MSE=22.57639
    left son=2 (45 obs) right son=3 (15 obs)
    Primary splits:
    Weight < 2567.5 to the right, improve=0.5953491, (0 missing)
    Node number 2: 45 observations, complexity param=0.1345282
    mean=22.46667, MSE=8.026667
    left son=4 (22 obs) right son=5 (23 obs)
    Primary splits:
    Weight < 3087.5 to the right, improve=0.5045118, (0 missing)
    Node number 3: 15 observations
    mean=30.93333, MSE=12.46222
    Node number 4: 22 observations
    mean=20.40909, MSE=2.78719
    Node number 5: 23 observations, complexity param=0.01282843
    mean=24.43478, MSE=5.115312
    left son=10 (15 obs) right son=11 (8 obs)
    Primary splits:
    Weight < 2747.5 to the right, improve=0.1476996, (0 missing)
    Node number 10: 15 observations
    mean=23.8, MSE=4.026667
    Node number 11: 8 observations
    mean=25.625, MSE=4.984375

plot（和 text）

在當前圖形裝置上將 rpart 物件繪製為決策樹。函式 text 對決策樹圖進行標註。

用法

    plot(object, uniform=FALSE, branch=1, compress=FALSE, nspace, margin=0, minbranch=.3, args)

其中 object 是一個 rpart 物件，uniform 如果為 TRUE，則使用節點的均勻垂直間距，branch 控制從父節點到子節點的支線的形狀，compress 如果為 FALSE，則葉節點將位於 1:nleaves 的水平繪圖座標處，如果為 TRUE，則例程將嘗試更緊湊地排列樹，nspace 是具有子節點的節點和葉節點之間的額外空間量，margin 是圍繞樹邊界留出的額外百分比的空白空間，minbranch 將分支的最小長度設定為 minbranch 乘以平均分支長度，args 是要傳遞給或從其他方法傳遞的引數。

示例

    fit <- rpart(Price ~ Mileage + Type + Country, cu.summary)
    plot(fit, compress=TRUE)
    text(fit, use.n=TRUE)

檔案：Third plot.png

post

建立 rpart 物件的 PostScript 演示圖。

用法

    plot(object, uniform=FALSE, branch=1, compress=FALSE, nspace, margin=0, minbranch=.3, args)

Object 是一個 rpart 物件，uniform 如果為 TRUE，則使用節點的均勻垂直間距，branch 控制從父節點到子節點的支線的形狀，compress 如果為 FALSE，則葉節點將位於 1:nleaves 的水平繪圖座標處，如果為 TRUE，則例程將嘗試更緊湊地排列樹，nspace 是具有子節點的節點和葉節點之間的額外空間量，margin 是圍繞樹邊界留出的額外百分比的空白空間，minbranch 將分支的最小長度設定為 minbranch 乘以平均分支長度，args 是要傳遞給或從其他方法傳遞的引數。

示例

    fit <- rpart(Mileage ~ Weight, car.test.frame)
    post(fit, file = "", title="Classification Tree for Wikibook")
    post(fit, file = "c:/output.ps", title = " Classification Tree for Wikibook")

檔案：Fourth plot.png

案例研究

場景和輸入資料

考慮下表中的關係資料庫，其模式由屬性 Play、Outlook、Temperature、Humidity 和 Windy 組成。決策樹允許預測屬性 Play 的值，前提是我們知道 Outlook、Humidity 和 Windy 等屬性的值。

天氣	溫度	溼度	風力	高爾夫球運動
晴朗	炎熱	高	無風	否
晴朗	炎熱	高	少量	否
多雲	炎熱	高	無風	是
雨	溫暖	高	無風	是
雨	寒冷	中等	無風	是
雨	寒冷	中等	少量	否
多雲	寒冷	中等	少量	是
晴朗	溫暖	高	無風	否
晴朗	寒冷	中等	無風	是
雨	溫暖	中等	無風	是
晴朗	溫暖	中等	少量	是
多雲	溫暖	高	少量	是
多雲	炎熱	中等	無風	是
雨	溫暖	高	少量	否

將資料匯入 R 很簡單。從第一行包含變數名稱的逗號分隔文字 (CSV) 檔案中，我們可以使用以下命令

    play_base <- read.table("path_to_the_file/play.csv", header=TRUE, sep=",")

我們可以使用命令 print(play_base) 或僅 play_base 檢視載入的表格，使用命令 "summary(play_base)" 檢視 rpart 物件的詳細列表

    Play    Outlook      Temperature   Humidity   Windy
    no :3   overcast:2   cool:5        high :4    false:7
    yes:7   rainy :4     hot :2        normal:6   true :3
            sunny :4     mild:3

執行和輸出

載入資料後，我們需要構建決策樹。屬性“Play”是要預測的結果。我們可以使用以下命令

    fit <- rpart(Play ~ Outlook + Temperature + Humidity + Wind, method="class", data=play_base,
    control=rpart.control(minsplit=1))

我們可以使用命令 summary(fit) 檢視載入的決策樹的詳細列表，使用命令 print(fit) 檢視決策樹

    1) root 10 3 yes (0.3000000 0.7000000)
      2) Temperature= mild 3 1 no (0.6666667 0.3333333)
        4) Outlook= sunny 2 0 no (1.0000000 0.0000000) *
        5) Outlook= overcast 1 0 yes (0.0000000 1.0000000) *
      3) Temperature= cool, hot 7 1 yes (0.1428571 0.8571429)
        6) Windy= true 1 0 no (1.0000000 0.0000000) *
        7) Windy= false 6 0 yes (0.0000000 1.0000000) *

以下命令將 rpart 物件繪製在當前圖形裝置上，作為決策樹

    plot(fit, uniform=TRUE, main="Decision Tree - Play?")
    text(fit, use.n=TRUE, all=TRUE, cex=.8)

檔案：Play or not play.png

玩還是不玩

分析

決策樹的構建始於對問題的描述，該描述應指定變數、操作以及決策過程的邏輯順序。在決策樹中，一個過程會導致一個或多個條件，這些條件可以導致操作或其他條件，直到所有條件確定一個特定操作，一旦構建，您就可以看到決策過程的圖形檢視。

為解決問題而生成的決策樹，描述的步驟順序確定以及天氣條件，驗證玩還是不玩是否是一個好的選擇。例如，在條件序列 (temperature = mild) -> (Outlook = overcast) -> play = yes 中，而在序列 (temperature = cold) -> (Windy = true) -> play = no 中。這表明決策樹是做出決定的絕佳工具。因此，這種分類方法可以成為獲取資訊的絕佳工具，這些資訊通常是組織不知道的，但對戰術和管理層極其重要。

參考文獻

Jiawei Han。資料探勘：概念與技術。Morgan Kaufmann 出版社，2001 年。

Mohammed J. Zaki 和 Wagner Meira Jr.. 資料探勘演算法基礎。劍橋大學出版社，2010 年。

Terry M. Therneau、Elizabeth J. Atkinson 和 Mayo 基金會。使用 RPART 例程的遞迴劃分簡介，1997 年。

R 語言定義 - [1]

R 簡介 - [2]

Quick-R - [3]

Terry M Therneau 和 Beth Atkinson。包“rpart”，2009 年。