R 中的資料探勘演算法/聚類/期望最大化 (EM)

本章旨在概述由 (儘管該技術是在文獻中非正式提出的，正如作者所建議的) 在 R-Project 環境中提出的期望最大化 (EM) 技術。第一部分介紹了代表性聚類和混合模型。第二部分將介紹演算法細節和一個案例研究。

將使用的 R 包是 Chris Fraley 和 Adrian Raftery 開發的 MCLUST-v3.3.2，可在 CRAN 庫中找到。MCLUST 工具是一個軟體，它包括以下功能：正態混合建模 (EM)；透過分層聚類方法進行 EM 初始化；基於貝葉斯資訊準則 (BIC) 估計聚類數量；以及顯示，包括不確定性圖和維投影。

本文件的資訊來源分為兩組：(i) R 和 MCLUST 的手冊和指南，包括技術報告 ，它是該專案的參考基礎，概述了 MCLUST，並提供了一些示例；(ii) 在文獻中找到的理論論文、調查和書籍。

簡介

聚類是指識別具有共同特徵且彼此凝聚且分離的實體組。由於在不同知識領域中的多種應用，人們對聚類的興趣日益濃厚。重點關注了在海量資料集中對客戶和產品的分組搜尋、Web 用法資料中的文件分析、來自微陣列的基因表達以及影像分析（其中聚類用於分割）。

聚類方法可以分為幾類。一種廣泛使用的方法是層次聚類，它最初認為每個點都代表一個組，並在每次迭代中合併兩個組，以最佳化某些標準。一個流行的標準是 提出的，包括組內平方和之和，由組之間的最短距離給出（單鏈接方法）。

另一個典型的類別是基於迭代重定位的，其中資料在每次迭代中從一個組移動到另一個組。由於使用為每個聚類建立的模型，該模型總結了組元素的特徵，因此也稱為代表性聚類。該類別中最流行的方法是 K-Means，由 提出，該方法基於使用平方和標準的迭代重定位。

在統計學和最佳化問題中，通常需要最大化或最小化特定空間中的函式及其變數。由於這些最佳化問題可能假設多種不同型別，每種型別都有其自身的特徵，因此已經開發了許多技術來解決它們。這些技術在資料探勘和知識發現領域非常重要，因為它可以作為大多數複雜而強大的方法的基礎。

其中一項技術是 最大似然，其主要目標是使用特定資料集調整統計模型，估計其未知引數，以便函式可以描述資料集中的所有引數。換句話說，該方法將使用資料集或已知分佈從統計模型中調整一些變數，以便模型可以“描述”每個資料樣本並估計其他資料樣本。

人們意識到聚類可以基於機率模型來覆蓋缺失值。這提供了有關資料應何時符合模型的見解，並已導致開發新的聚類方法，例如期望最大化 (EM)，該方法基於有限混合模型中未觀察變數的最大似然原理。

討論的技術

EM 演算法是一種無監督的聚類方法，即不需要訓練階段，基於混合模型。它遵循一種迭代方法，次優，試圖找到其屬性具有最大似然的機率分佈的引數。

一般來說，演算法的輸入是資料集 (x)，聚類總數 (M)，接受的收斂誤差 (e) 和最大迭代次數。對於每次迭代，首先執行 E-Step (Expectation)，它估計每個點屬於每個聚類的機率，然後執行 M-Step (Maximization)，它重新估計每個類的機率分佈的引數向量。當分佈引數收斂或達到最大迭代次數時，演算法結束。

演算法

初始化

M 個類（或聚類）中的每個類 j 都由一個引數向量 (θ) 組成，該向量由均值 ($\mu _{j}$) 和協方差矩陣 ($P_{j}$) 組成，它代表用於表徵觀察到的和未觀察到的資料集 x 實體的高斯機率分佈（正態）的特徵。

$\theta (t)=(\mu _{j}(t),\ P_{j}(t)),\ j\ =\ 1,...,M$

在初始時刻 (t = 0) ，實現可以隨機生成均值（$\mu _{j}$）和協方差矩陣（$P_{j}$）的初始值。EM 演算法旨在逼近真實分佈的引數向量 (θ)。MCLUST 提供的另一種選擇是用層次聚類技術獲得的聚類來初始化 EM。

E 步

這一步負責估計每個元素屬於每個聚類的機率（$P(C_{j}|x_{k})$）。每個元素都由一個屬性向量組成（$x_{k}$）。每個聚類中點的相關程度由每個元素屬性的可能性與其在聚類 $C_{j}$ 中其他元素的屬性的比較給出。

$P(C_{j}|x)={\frac {|\sum _{j}(t)|^{-{\frac {1}{2}}}\ e^{n_{j}}\ P_{j}(t)}{\sum _{k=1}^{M}\ |\sum _{j}(t)|^{-{\frac {1}{2}}}\ e^{n_{j}}\ P_{k}(t)}}}$

M 步

這一步負責估計每類機率分佈的引數，以便進行下一步操作。首先計算透過所有點在每個點相關程度函式上的平均值獲得的類別 j 的均值（μj）。

$\mu _{j}(t+1)={\frac {\sum _{k=1}^{N}\ P(C_{j}|x_{k})\ x_{k}}{\sum _{k=1}^{N}\ P(C_{j}|x_{k})}}$

為了計算下一個迭代的協方差矩陣，應用貝葉斯定理，這意味著 $P(A|B)=(P(B|A)*P(A))/P(B)$，基於類發生條件機率。

$\sum _{j}(t+1)={\frac {\sum _{k=1}^{N}\ P(C_{j}|x_{k})\ (x_{k}-\mu _{j}(t))\ (x_{k}-\mu _{j}(t))}{\sum _{k=1}^{N}\ P(C_{j}|x_{k})}}$

每個類的出現機率是透過機率的平均值計算的（$C_{j}$）作為每個點從類的相關度函式。

$P_{j}(t+1)={\frac {1}{N}}\sum _{k=1}^{N}P(C_{j}|x_{k})$

屬性表示引數向量 θ，它表徵每個類的機率分佈，將在下一次演算法迭代中使用。

收斂測試

在每次迭代執行後，將進行收斂測試，以驗證迭代的屬性向量與前一次迭代的屬性向量之間的差異是否小於引數給定的可接受誤差容限。一些實現使用類分佈平均值之間的差異作為收斂標準。

if(||θ(t + 1) − θ(t)|| < ǫ)
   stop
else
   call E-Step
end

該演算法具有在每一步估計具有最大區域性似然性的新屬性向量的特性，但不一定是全域性的，這降低了它的複雜性。但是，根據資料的離散程度和資料量，演算法可能會因為定義的最大迭代次數而停止。

實施

包

R 中的期望最大化演算法， 在 中提出，將使用 mclust 包。此包包含執行聚類演算法的關鍵方法，包括用於 E 步和 M 步計算的函式。包手冊解釋了其所有函式，包括簡單的示例。此手冊可在 中找到。

mclust 包還為 EM 提供了各種模型，也為層次聚類 (HC) 提供了模型，它由協方差結構定義。這些模型在表 1 中列出，並在 中詳細解釋。

表 1：協方差矩陣結構。

識別符號	模型	HC	EM	分佈	體積	形狀	方向
E		*	*	(單變數)	相等
V		*	*	(單變數)	可變
EII	$\lambda I$	*	*	球形	相等	相等	NA
VII	$\lambda _{k}I$	*	*	球形	可變	相等	NA
EEI	$\lambda A$		*	對角線	相等	相等	座標軸
VEI	$\lambda _{k}A$		*	對角線	可變	相等	座標軸
EVI	$\lambda A_{k}$		*	對角線	相等	可變	座標軸
VVI	$\lambda _{k}A_{k}$		*	對角線	可變	可變	座標軸
EEE	$\lambda DAD^{T}$	*	*	橢圓形	相等	相等	相等
EEV	$\lambda D_{k}AD_{k}^{T}$		*	橢圓形	相等	相等	可變
VEV	$\lambda _{k}D_{k}AD_{k}^{T}$		*	橢圓形	可變	相等	可變
VVV	$\lambda _{k}D_{k}A_{k}D_{k}^{T}$	*	*	橢圓形	可變	可變	可變

執行演算法

函式“em”可用於執行期望最大化方法，因為它實現了引數化高斯混合模型（GMM）的該方法，從E步開始。該函式使用以下引數

• 模型名稱：所用模型的名稱；

• 資料：所有收集的資料，必須都是數值型。如果資料格式用矩陣表示，則行表示樣本（觀測值），列表示變數；

• 引數：模型引數，可以取以下值：pro、mean、variance 和 Vinv，分別對應於混合的各個組成部分的混合比例、每個組成部分的均值、引數方差和資料區域的估計超體積。

• 其他：與主題無關的引數，此處不作描述。更多詳細資訊可以在包手冊中找到。

執行完後，函式將返回

• 模型名稱：模型名稱；
• z：一個矩陣，其在位置[I,k]的元素表示第i個樣本屬於第k個混合分量的條件機率；
• 引數：與輸入相同；
• 其他：其他指標，此處不作討論。更多詳細資訊可以在包手冊中找到。

一個簡單的例子

為了演示如何使用R來執行期望最大化方法，以下演算法提供了一個測試資料集的簡單示例。該示例也可以在包手冊中找到。

> modelName = ``EEE''
> data = iris[,-5]
> z = unmap(iris[,5])
> msEst <- mstep(modelName, data, z)
> names(msEst)
> modelName = msEst$modelName
> parameters = msEst$parameters
> em(modelName, data, parameters)

第一行執行M步，以便生成在em函式中使用的引數。該函式稱為mstep，其輸入是模型名稱，如“EEE”，資料集為iris資料集，最後是z矩陣，該矩陣包含每個類包含每個資料樣本的條件機率。該z矩陣由unmap函式生成。

執行完M步後，演算法將顯示（第2行）此函式返回的物件的屬性。第三行將使用M步方法的一些結果作為輸入開始聚類過程。

聚類方法將返回在該過程中估計的引數以及每個樣本落入每個類的條件機率。這些引數包括均值和方差，最後一個對應於使用mclustVariance方法。

檢視

本節將介紹MCLUST包中提供的一些視覺化示例。首先將展示一個從選擇簇數、初始化和分割槽等方面展示聚類整體過程的簡單示例。然後將解釋一個使用兩個隨機混合與兩個高斯混合進行比較的教學示例。

基本示例

這是一個簡單的示例，用於展示MCLUST包提供的功能。它應用於faithful資料集（包含在R專案中）。首先，聚類分析估計最能代表該資料集的簇數以及點擴散的協方差結構。這是透過稱為貝葉斯資訊準則（BIC）的技術來執行的，該技術將簇數從1變為9。BIC是最大化對數似然的值，用模型中引數數量的懲罰來衡量。然後執行層次聚類技術（HC），該技術不需要初始化階段。HC的輸出，即每個元素所屬的簇，被用來初始化期望最大化技術（EM）。執行完EM聚類後，將在下面顯示圖表

### basic_example.R ###
# usage: R --no-save < basic_example.R

library(mclust)           # load mclust library
x = faithful[,1]          # get the first column of the faithful data set
y = faithful[,2]          # get the second column of the faithful data set
plot(x,y)                 # plot the spread points before the clustering
model <- Mclust(faithful) # estimate the number of cluster (BIC), initialize (HC) and clusterize (EM)
data = faithful           # get the data set 
plot(model, faithful)     # plot the clustering results

檔案:Basic points.pdf

教學示例

為了展示兩種不同的場景，開發了一個教學示例：（a）模型不代表資料；（b）資料符合模型。本示例旨在展示EM在帶噪聲和乾淨的資料集中是如何工作的。

a) 均勻隨機混合

透過一個均勻隨機函式生成一個帶噪聲的資料集。點的擴散在圖表中顯示。然後使用預設引數執行聚類分析（即將簇數從1變為9）。聚類工具顯示一條警告訊息，提示最佳模型出現在最小值或最大值處，在本例中，所有點都被分組到一個簇中，因此是最小值。

### random_example.R ###
# usage: R --no-save < random_example.R

library(mclust)                  # load mclust library
x1 = runif(20)                   # generate 20 random random numbers for x axis (1st class)
y1 = runif(20)                   # generate 20 random random numbers for y axis (1st class)
x2 = runif(20)                   # generate 20 random random numbers for x axis (2nd class)
y2 = runif(20)                   # generate 20 random random numbers for y axis (2nd class)
rx = range(x1,x2)                # get the axis x range
ry = range(y1,y2)                # get the axis y range
plot(x1, y1, xlim=rx, ylim=ry)   # plot the first class points
points(x2, y2 )                  # plot the second class points
mix = matrix(nrow=40, ncol=2)    # create a dataframe matrix 
mix[,1] = c(x1, x2)              # insert first class points into the matrix
mix[,2] = c(y1, y2)              # insert second class points into the matrix
mixclust = Mclust(mix)           # initialize EM with hierarchical clustering, execute BIC and EM

# Warning messages:
# 1: In summary.mclustBIC(Bic, data, G = G, modelNames = modelNames) :
#    best model occurs at the min or max # of components considered
# 2: In Mclust(mix) : optimal number of clusters occurs at min choice

b) 兩個高斯混合

此場景由兩個透過高斯分佈函式（正態分佈）生成並分離良好的資料集組成。點在第一個圖表中顯示。應用了EM聚類，結果也顯示在下面的圖表中。正如我們所看到的，EM聚類獲得了兩個符合資料的符合資料的兩個高斯模型。

### gaussian_example.R ###
# usage: R --no-save < gaussian_example.R

library(mclust)                  # load mclust library
x1 = rnorm(n=20, mean=1, sd=1)   # get 20 normal distributed points for x axis with mean=1 and std=1 (1st class)
y1 = rnorm(n=20, mean=1, sd=1)   # get 20 normal distributed points for x axis with mean=1 and std=1 (2nd class)
x2 = rnorm(n=20, mean=5, sd=1)   # get 20 normal distributed points for x axis with mean=5 and std=1 (1st class)
y2 = rnorm(n=20, mean=5, sd=1)   # get 20 normal distributed points for x axis with mean=5 and std=1 (2nd class)
rx = range(x1,x2)                # get the axis x range
ry = range(y1,y2)                # get the axis y range
plot(x1, y1, xlim=rx, ylim=ry)   # plot the first class points
points(x2, y2)                   # plot the second class points
mix = matrix(nrow=40, ncol=2)    # create a dataframe matrix 
mix[,1] = c(x1, x2)              # insert first class points into the matrix
mix[,2] = c(y1, y2)              # insert second class points into the matrix
mixclust = Mclust(mix)           # initialize EM with hierarchical clustering, execute BIC and EM
plot(mixclust, data = mix)       # plot the two distinct clusters found

檔案:Gaussian density.pdf 檔案:Gaussian uncertainty.pdf

案例研究

場景

要分析的場景由MCLUST包中名為“wreath”的樣本資料集組成。進行更詳細的聚類分析，應用於由14個點組成的場景，超過了預設MCLUST引數允許的最大簇數。聚類技術執行兩次：（i）第一次基於預設MCLUST；（ii）使用自定義引數。

輸入資料

該案例研究的輸入是 MCLUST 包提供的 wreath 資料集。該資料集包含 14 個點組，如下圖所示，可以使用球形或橢圓形對其進行建模，考慮到資料旋轉導致的取向。

### case_input.R ###
# usage: R --no-save < case_default.R

plot(wreath[,1],wreath[,2])

執行

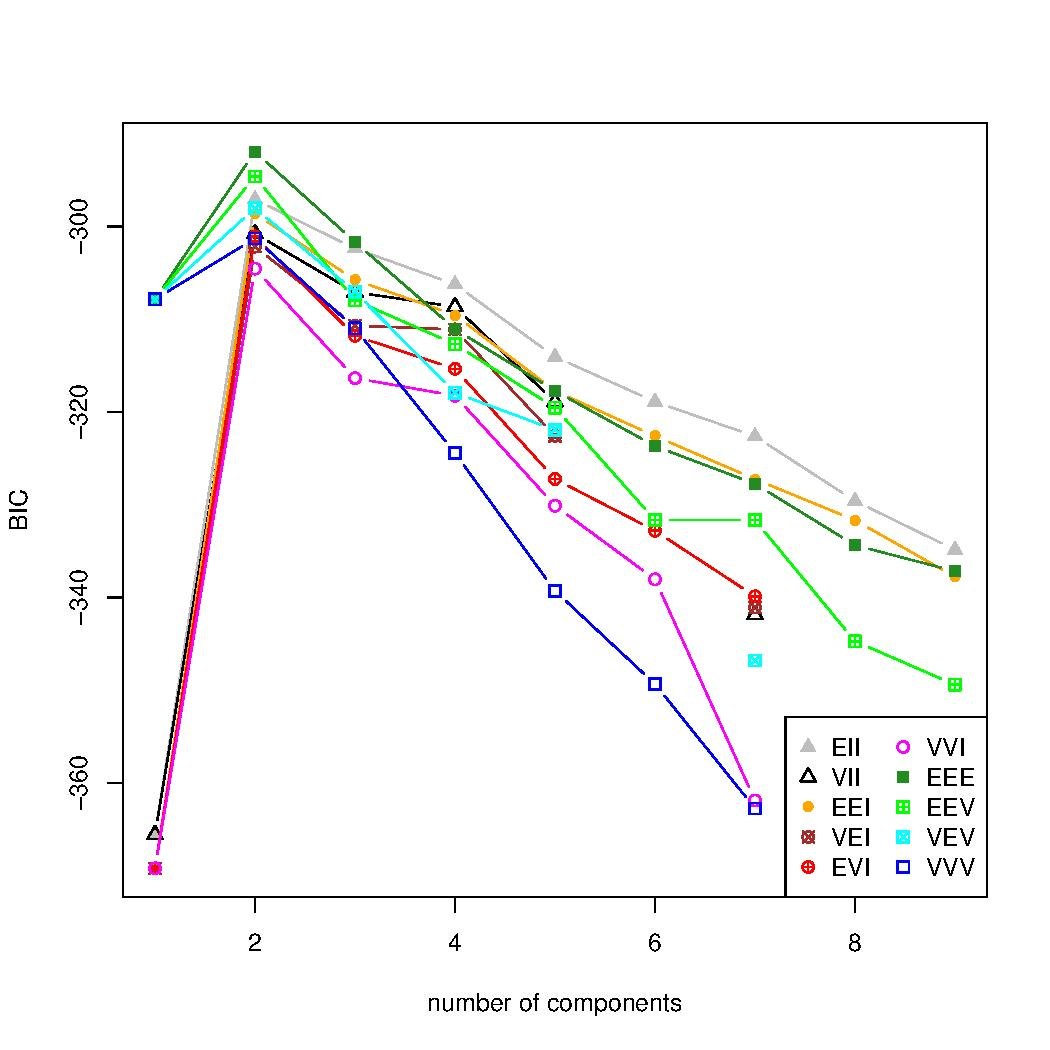
聚類執行了兩次。第一次基於 MCLUST 工具提供的預設引數，將聚類數量從 1 變化到 9，這比擬合案例研究資料集所需的聚類數量要少。聚類數量的估計顯示在一個圖表中，該圖表改變聚類數量並計算每個值的貝葉斯資訊準則 (BIC)。我們可以看到，使用預設引數的 BIC 是發散的，而預期是找到一個峰值，然後下降，表明最佳的聚類數量。

### case_default.R ###
# usage: R --no-save < case_default.R

library(mclust)

wreathBIC <- mclustBIC(wreath)
plot(wreathBIC, legendArgs = list(x = "topleft"))

然後，聚類數量被定製，修改為從 1 變化到 20，如下所示。BIC 技術將給出最佳的聚類數量，在本例中為 14 個聚類，以及具有該資料集屬性的係數結構，即 EEV，這意味著聚類具有相似的形狀、相似的體積，但不同的方向。再次執行 BIC 方法後，我們可以看到，由圖表中的峰值指示的 14 個聚類，是呈現該資料最大似然性的聚類數量。

### case_customized.R ###
# usage: R --no-save < case_customized.R

library(mclust)
wreathDefault <- mclustBIC(wreath)
wreathCustomize <- mclustBIC(wreath, G = 1:20, x = wreathDefault)
plot(wreathCustomize, G = 10:20, legendArgs = list(x = "bottomleft"))
summary(wreathCustomize, wreath)

輸出

該聚類的輸出使用下圖中所示的 mclust2Dplot 方法進行分析。使用了密度視覺化。找到的聚類以 14 個模型為特徵，這些模型具有橢圓體的分佈，方向不同，與資料一致。方法摘要可以稍後執行，以分析聚類結果的其他方面。

### case_output.R ###
# usage: R --no-save < case_customized.R

library(mclust)
data(wreath)
wreathBIC <- mclustBIC(wreath)
wreathBIC <- mclustBIC(wreath, G = 1:20, x = wreathBIC)
wreathModel <- summary(wreathBIC, data = wreath)
mclust2Dplot(data = wreath, what = "density", identify = TRUE, parameters = wreathModel$parameters, z = wreathModel$z)

分析

我們可以看到，建立用來表示點的混合模型與資料集相符。在本例中，各組之間沒有交集，因此所有點都被正確分類。聚類方向允許該方法找到更好的橢圓形來表示這些點。

我們得出結論，儘管依賴於聚類數量和初始化階段，EM 聚類技術仍然是一種有效的方法，可以為多種資料分散場景產生良好的結果。使用 BIC 估計聚類數量，以及使用層次聚類 (HC)（不依賴於聚類數量）初始化聚類，可以提高結果的質量。