待辦事項
本節仍在編寫中。但歡迎您新增您的貢獻或以任何方式提供幫助

介紹

層次聚類方法包括將資料物件分組到一個簇樹中。主要有兩種技術型別：自下而上和自上而下方法。第一種方法從由單個物件組成的較小的簇開始，並在每一步中，將當前簇依次合併成更大的簇，直到形成由所有資料物件組成的簇。第二種方法使用相同的邏輯，但方向相反，從包含所有物件的最大的簇開始，並依次將其拆分成更小的簇，直到形成單例組。除了策略之外，另一個重要問題是用於構建（合併或拆分）簇的度量。這些度量可以是不同的距離度量，將在下一節中介紹。

簇間度量

以下是四種廣泛使用的用於度量簇間距離的度量。其中 p 和 p' 是兩個不同的資料物件點，m_i 是簇 C_i 的均值，n_i 是簇 C_i 中物件的個數，|p - p'| 是 p 和 p' 之間的距離。

最小距離: $d_{min}(C_{i},C_{j})=min_{p\in C_{i},p'\in C_{j}}\mid p-p'\mid$

最大距離: $d_{max}(C_{i},C_{j})=max_{p\in C_{i},p'\in C_{j}}\mid p-p'\mid$

平均距離: $d_{mean}(C_{i},C_{j})=\mid m_{i}-m_{j}\mid$

平均距離: $d_{avg}(C_{i},C_{j})={\frac {1}{n_{i}n_{j}}}\sum _{p\in C_{i}}\sum _{p'\in C_{j}}\mid p-p'\mid$

演算法

一種實現自下而上方法的演算法是 AGNES (AGglomerative NESting)。AGNES 的主要思想是在第一步中建立由單個數據物件組成的簇，然後使用指定的度量（如上一節提到的那些度量），將這些簇合併成更大的簇。第二步被迭代重複，直到只獲得一個簇，該簇包含所有資料物件。實現這種方法的另一個演算法示例是 Cure，它在處理所有實體時，將簇縮小到其中心。

DIANA (DIvisive ANAlysis) 是一個實現自上而下方法的演算法示例，該演算法從包含所有元素的單個大簇開始，並迭代地將當前組拆分成更小的組。與 AGNES 和 Cure 一樣，需要定義一些度量來計算簇間距離，以便決定如何（在何處）拆分它們。

實現

為了在 R 中使用層次聚類演算法，必須安裝 cluster 包。該包包含一個函式，可以根據不同的演算法執行 AGNES 過程和 DIANA 過程。

AGNES 函式

cluster 包提供的 AGNES 函式，可以使用如下方法：

agnes(x, diss = inherits(x, "dist"), metric = "euclidean", stand = FALSE, method = "average", par.method, keep.diss = n < 100, keep.data = !diss)

其中引數是

x: 資料矩陣或資料框（所有變數必須為數值型，允許缺失值），或不相似的矩陣（不允許缺失值），具體取決於diss引數的值。
diss: 邏輯標誌。如果為 TRUE（對於 dist 或 dissimilarity 物件的預設值），則x被認為是不相似性矩陣。如果為 FALSE，則x被視為觀測值與變數的矩陣。
metric: 字串，指定用於計算觀測值之間不相似的度量。當前可用的選項為euclidean和manhattan。歐氏距離是差值的平方根之和，曼哈頓距離是絕對差值的總和。如果x已經是距離矩陣，則此引數將被忽略。
stand: 邏輯標誌：如果為 TRUE，則在計算不相似的距離之前，x中的測量值將被標準化。測量值會針對每個變數（列）進行標準化，方法是減去變數的平均值併除以變數的平均絕對偏差。如果x已經是距離矩陣，則此引數將被忽略。
method: 字串，定義聚類方法。實現的六種方法為average（[未加權配對]組平均方法，UPGMA）、single（單鏈接）、complete（完全連結）、ward（Ward 方法）、weighted（加權平均連結）及其推廣flexible，它使用 Lance-Williams 公式和 par.method 引數的（常數版本）。預設值為average。
par.method: 如果 method = flexible，則為長度為 1、3 或 4 的數值向量。
keep.diss, keep.data: 邏輯值，指示是否應在結果中保留不相似的距離和/或輸入資料x。將這些值設定為 FALSE 可以得到更小的結果，從而節省記憶體分配時間。

AGNES 演算法具有以下特點

生成聚類係數，該係數衡量所發現的聚類結構的程度
提供層次樹和標語，這是一種新穎的圖形顯示

AGNES 函式返回一個agnes 物件，代表聚類。此 agnes 物件是一個列表，包含以下元件

order: 向量，提供原始觀測值的排列，以便於繪圖
order.lab: 與 order 類似的向量，但包含觀測值標籤，而不是觀測值編號。此元件僅在原始觀測值被標記的情況下可用。
height: 向量，包含在連續階段合併聚類之間的距離。
ac: 聚類係數，衡量資料集的聚類結構。
merge: (n-1) x 2 矩陣，其中n是觀測值的個數。
diss: dissimilarity 類的物件，表示資料集的總不相似的距離矩陣。
data: 矩陣，包含原始或標準化的測量值。這僅在輸入結構與距離矩陣不同時可用。

視覺化

可以使用print和plot函式來視覺化 AGNES 函式的結果。

第一個函式只打印agnes物件的元件，第二個函式繪製該物件，建立一個代表資料的圖表。

以下是用 plot 函式的示例

plot(x, ask = FALSE, which.plots = NULL, main = NULL,sub = paste("Agglomerative Coefficient = ",round(x$ac, digits = 2)),adj = 0, nmax.lab = 35, max.strlen = 5, xax.pretty = TRUE, ...)

使用的引數為

x: agnes 物件
ask: 如果為 TRUE 且 which.plots = NULL，則 plot.agnes 透過選單進行互動模式操作。
which.plots: 整數向量或 NULL（預設值），後者生成兩個圖
main, sub: 圖的標題和副標題，每個都帶有一個方便的預設值。
adj: 用於調整標語圖中的標籤
nmax.lab: 整數，指示被認為過大而無法在標語圖中使用單名稱標記的標籤數量。
max.strlen: 正整數，指示在標語圖標籤中字串被截斷的長度。
xax.prety: 正整數，指示在標語圖標籤中字串被截斷的長度。
...: 圖形引數。

以下是用 print 函式的示例

print(x, ...)

引數為

x: agnes 物件
...: 潛在的進一步引數（通用函式 print 需要）

DIANA 函式

cluster 包提供的 DIANA 函式可以用如下方式使用

diana(x, diss = inherits(x, "dist"), metric = "euclidean", stand = FALSE, keep.diss = n < 100, keep.data = !diss)

其中引數是

x: 資料矩陣或資料框（所有變數必須為數值型，允許缺失值），或不相似的矩陣（不允許缺失值），具體取決於diss引數的值。
diss: 邏輯標誌。如果為 TRUE（對於 dist 或 dissimilarity 物件的預設值），則x被認為是不相似性矩陣。如果為 FALSE，則x被視為觀測值與變數的矩陣。
metric: 字串，指定用於計算觀測值之間不相似的度量。當前可用的選項為euclidean和manhattan。歐氏距離是差值的平方根之和，曼哈頓距離是絕對差值的總和。如果x已經是距離矩陣，則此引數將被忽略。
stand: 邏輯值；如果為 true，則在計算不相似的距離之前，x中的測量值將被標準化。測量值會針對每個變數（列）進行標準化，方法是減去變數的平均值併除以變數的平均絕對偏差。如果 x 已經是距離矩陣，則此引數將被忽略。
keep.diss, keep.data: 邏輯值，指示是否應在

結果中保留不相似的距離和/或輸入資料x。將這些值設定為 FALSE 可以得到更小的結果，從而節省記憶體分配時間。

DIANA 演算法在計算分裂層次結構方面可能很獨特，而大多數其他用於層次聚類的軟體都是聚合的。它與 AGNES 函式具有以下相同的功能

生成聚類係數，該係數衡量所發現的聚類結構的程度
提供層次樹和標語，這是一種新穎的圖形顯示

DIANA 函式返回一個diana 物件，代表聚類。此 agnes 物件是一個列表，包含以下元件

order: 向量，提供原始觀測值的排列，以便於繪圖
order.lab: 與 order 類似的向量，但包含觀測值標籤，而不是觀測值編號。此元件僅在原始觀測值被標記的情況下可用。
heigh: 向量，包含在連續階段合併聚類之間的距離。
dc: 分裂係數，衡量資料集的聚類結構。
merge: (n-1) x 2 矩陣，其中n是觀測值的個數。
diss: dissimilarity 類的物件，表示資料集的總不相似的距離矩陣。
data: 矩陣，包含原始或標準化的測量值。這僅在輸入結構與距離矩陣不同時可用。

視覺化

可以使用print和plot函式來視覺化 DIANA 函式的結果。

第一個函式只打印agnes物件的元件，第二個函式繪製該物件，建立一個代表資料的圖表。

以下是用plot函式的示例

plot(x, ask = FALSE, which.plots = NULL, main = NULL, sub = paste("Divisive Coefficient = ", round(x$dc, digits = 2)), adj = 0, nmax.lab = 35, max.strlen = 5, xax.pretty = TRUE, ...)

使用的引數為

x: diana 物件
ask: 如果為 TRUE 且 which.plots = NULL，則 plot.diana 透過選單進行互動模式操作。
which.plots: 整數向量或 NULL（預設值），後者生成兩個圖
main, sub: 圖的標題和副標題，每個都帶有一個方便的預設值。
adj: 用於調整標語圖中的標籤
nmax.lab: 整數，指示被認為過大而無法在標語圖中使用單名稱標記的標籤數量。
max.strlen: 正整數，指示在標語圖標籤中字串被截斷的長度。
xax.prety: 正整數，指示在標語圖標籤中字串被截斷的長度。
...: 圖形引數。

以下是用print函式的示例

print(x, ...)

引數為

x: diana 物件
...: 潛在的進一步引數（通用函式 print 需要）

用例

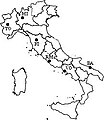
在本節中，將說明在一些義大利城市中使用層次聚類的示例。在以下示例中，將使用平均距離或單鏈接方法。

場景

給定義大利城市之間的公里距離，目標是將它們聚合到叢集中。例如，在 R 中使用agnes函式。

輸入資料

輸入資料是一個表格，包含義大利城市之間距離的數值。該表格包含六列（和行），代表義大利城市。每個單元格都有一個數值，代表它們之間的公里距離。該表格可以從電子表格或文字檔案中載入。

圖 1 說明了本示例中使用的城市。

圖 1

輸入距離矩陣

	BA	FI	MI	VO	RM	TO
BA	0	662	877	255	412	996
FI	662	0	295	468	268	400
MI	877	295	0	754	564	138
VO	255	468	754	0	219	869
RM	412	268	564	219	0	669
TO	996	400	138	869	669	0

執行

agnes 函式可以用如下方式用於定義國家組

# import data
x <- read.table("data.txt")

# run AGNES
ag <- agnes (x, false, metric="euclidean", false, method ="single")
 
# print components of ag
print(ag)

# plot clusters
plot(ag, ask = FALSE, which.plots = NULL)

agnes 的第二個引數的值為 FALSE，因為x被視為觀測值與變數的矩陣。第四個引數也為 FALSE，因為不需要對每列進行標準化。

輸出

以下是列印函式應用返回的agnes類元件的結果

Call:    agnes(x = x, diss = FALSE, metric = "euclidean", stand = FALSE,      method = "single") 
Agglomerative coefficient:  0.3370960 
Order of objects:
[1] BA VO RM FI MI TO
Height (summary):
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  295.8   486.0   486.5   517.6   642.6   677.0 

Available components:
[1] "order"     "height"    "ac"        "merge"     "diss"      "call"     
[7] "method"    "order.lab" "data"

以下是繪製函式應用返回的類結果

樹狀圖

分析

該演算法總是將最近的城市對進行聚類，因此，在這種情況下，“鄰里”城市首先被聚類。在單鏈接聚類中，規則是複合物件到另一個物件的距離等於叢集中任何成員到外部物件的最小距離。

然而，凝聚式聚類方法有一些缺點

它們不能很好地擴充套件：時間複雜度至少為O( $n^{2}$ )，其中n是總物件數；
它們永遠無法撤銷之前所做的事情。

參考文獻

J. Han and M. Kamber. Data Mining: Concepts and Techniuqes. Morgan Kaufmann Publishers, San Francisco, CA, 2006.

Maechler, M. Package 'cluster'. Disponível em <http://cran.r-project.org/web/packages/cluster/cluster.pdf> Acesso em 12 dez 2009.

Meira Jr., W.; Zaki, M. Fundamentals of Data Mining Algorithms. Disponível em <http://www.dcc.ufmg.br/miningalgorithms/DokuWiki/doku.php> Acesso em 12 dez 2009.

A Tutorial on Clustering Algorithms. Disponível em <http://home.dei.polimi.it/matteucc/Clustering/tutorial_html/hierarchical.html>. Acesso em 12 dez 2009.