R 中的資料探勘演算法/降維/主成分分析
本章介紹主成分分析(PCA)技術及其在 R 專案中的應用,用於統計計算。首先,我們將介紹該技術及其演算法,然後我們將展示如何使用 R 語言實現 PCA 以及如何使用它。最後,我們將以資料探勘場景為例展示該技術在資料探勘中的應用。本章末尾將提供進一步的資訊參考。
PCA 是一種降維方法,其中對因素之間的協方差進行分析。原始資料將根據資料中的方差重新對映到新的座標系中。PCA 應用一種數學方法,將許多(可能)相關的變數轉換為數量較少的無關變數,稱為主成分。第一個主成分解釋了資料中儘可能多的可變性,每個後續成分解釋了儘可能多的剩餘可變性。
當資料包含大量變數時,PCA 很有用,而且(可能)這些變數之間存在一些冗餘。在這種情況下,冗餘意味著某些變數彼此相關。由於這種冗餘,PCA 可用於將觀察到的變數減少為更少數量的主成分,這些主成分將解釋觀察到的變數中大部分的方差。
PCA 被推薦作為一種探索性工具,用於發現數據中未知的趨勢。該技術已在人臉識別和影像壓縮等領域得到應用,並且是發現高維資料模式的常用技術。
PCA 演算法包含 5 個主要步驟
- 減去平均值:從每個資料維減去平均值。減去的平均值是每個維的平均值。這將生成一個平均值為零的資料集。
- 計算協方差矩陣
- 其中 是一個矩陣,每個條目都是計算兩個獨立維度之間的協方差的結果。
- 計算協方差矩陣的特徵向量和特徵值。
- 選擇成分並形成特徵向量:從協方差矩陣中找到特徵向量後,下一步是按特徵值對它們進行排序,從高到低。這樣,成分將按重要性排序。您選擇的特徵向量數量將是新資料集的維度數量。此步驟的目標是構建特徵向量(向量矩陣)。從特徵向量列表中,選擇您選擇的特徵向量,並使用它們形成一個列矩陣。
- FeatureVector = (eig_1, eig_2, ..., eig_n)
- 推匯出新資料集。取 FeatureVector 的轉置,並將其乘以原始資料集的左側,轉置
- FinalData = RowFeatureVector x RowDataAdjusted
- 其中 RowFeatureVector 是一個矩陣,其列是特徵向量的轉置(特徵向量現在位於行中,最重要的特徵向量位於頂部),而 RowDataAdjusted 是平均值調整後的資料轉置(資料項位於每個列中,每行包含一個單獨的維度)。
在本教程中,我們從 stats 包中選擇了 princomp 方法。
- R 包:stats
- 方法:princomp
- 文件:princomp
princomp 是一種泛型方法,具有來自 stats 包的“formula”和“default”方法,它對給定的數值資料矩陣執行主成分分析,並將結果作為 princomp 類的物件返回。
用法
princomp(x, ...)
- 類“formula”的 S3 方法
princomp(formula, data = NULL, subset, na.action, ...)
- 預設 S3 方法
princomp(x, cor = FALSE, scores = TRUE, covmat = NULL, subset = rep(TRUE, nrow(as.matrix(x))), ...)
- 類“princomp”的 S3 方法
predict(object, newdata, ...)
引數
- formula
- 一個沒有響應變數的公式,僅引用數值變數。
- data
- 一個可選資料框,包含公式 formula 中的變數。預設情況下,變數取自 environment(formula)
- subset
- 一個可選向量,用於選擇資料矩陣 x 的行(觀測值)。
- na.action
- 一個函式,指示資料包含 NA 時應該發生什麼。預設值由 options 的 na.action 設定確定,如果未設定,則為 na.fail。'factory-fresh' 預設值為 na.omit。
- x
- 一個數值矩陣或資料框,提供用於主成分分析的資料。
- cor
- 一個邏輯值,指示計算應該使用相關矩陣還是協方差矩陣。(如果不存在常數變數,則只能使用相關矩陣。)
- scores
- 一個邏輯值,指示是否應計算每個主成分的分數。
- covmat
- 一個協方差矩陣,或一個由 cov.wt(以及來自 MASS 包的 cov.mve 或 cov.mcd)返回的協方差列表。如果提供,將使用它而不是 x 的協方差矩陣。
- ...
- 傳遞給其他方法的引數,或從其他方法傳遞的引數。如果 x 是一個公式,則可以指定 cor 或 scores。
- object
- 繼承自“princomp”的類的物件
- newdata
- 一個可選資料框或矩陣,用於查詢用於預測的變數。如果省略,將使用得分。如果原始擬合使用了一個公式或一個數據框或一個具有列名的矩陣,那麼 newdata 必須包含具有相同名稱的列。否則,它必須包含相同數量的列,以便按相同的順序使用。
價值
princomp 方法返回一個包含以下元件的“princomp”類列表
- sdev
- 一個沒有響應變數的公式,僅引用數值變數。
- loadings
- 變數載荷矩陣(即,一個矩陣,其列包含特徵向量)。
- center
- 減去的均值。
- scale
- 應用於每個變數的縮放比例。
- n.obs
- 觀察的數量。
- scores
- 如果 scores = TRUE,則提供的資料在主成分上的得分。這些值僅在提供 x 時才非空,並且如果也提供了 covmat,則它是一個協方差列表。對於公式方法,napredict() 被應用於處理由 na.action 省略的值。
- call
- 匹配的呼叫。
- na.action
- 如果相關。
這些物件的 print 方法以良好的格式列印結果,而 plot 方法則生成螢幕圖。 還有一個 biplot 方法。
例子
require(graphics)
summary(pc.cr <- princomp(USArrests, cor = TRUE))
loadings(pc.cr)
plot(pc.cr)
biplot(pc.cr)
為了說明 PCA 降維技術,將展示一個簡單的案例研究。
在資訊檢索 (IR) 領域,查詢和文件可以在向量空間中表示。 一般來說,使用多個特徵來描述查詢檢索到的文件,例如 TF-IDF 和 PageRank 措施。
偶爾,可能需要將文件視覺化到二維空間中。 為此,可以使用 PCA。
最近,微軟釋出了 LETOR 基準資料集,用於研究 LEarning TO Rank,其中包含標準特徵、相關性判斷、資料分割槽、評估工具和多個基線。 LETOR 包含多個數據集,用於從兩個查詢集和 Gov2 網頁集合派生的排序設定。 採用 5 折交叉驗證策略,並將 5 折分割槽包含在包中。 在每一折中,有三個用於學習的子集:訓練集、驗證集和測試集。 可以從 LETOR 網站 下載資料集。
LETOR 資料集中典型的文件如下描述
0 qid:1 1:1.000000 2:1.000000 3:0.833333 4:0.871264 5:0 6:0 7:0 8:0.941842 9:1.000000 10:1.000000 11:1.000000 12:1.000000 13:1.000000 14:1.000000 15:1.000000 16:1.000000 17:1.000000 18:0.719697 19:0.729351 20:0 21:0 22:0 23:0.811565 24:1.000000 25:0.972730 26:1.000000 27:1.000000 28:0.922374 29:0.946654 30:0.938888 31:1.000000 32:1.000000 33:0.711276 34:0.722202 35:0 36:0 37:0 38:0.798002 39:1.000000 40:1.000000 41:1.000000 42:1.000000 43:0.959134 44:0.963919 45:0.971425 #docid = 244338
LETOR 檔案無法“按原樣”匯入,但使用以下指令碼,可以將 LETOR 格式轉換為 R 接受的其他格式,如下所示
cat train.txt | grep "qid:1 " | gawk '{ printf("doc_"$50); for (i=3;i<=47;i++) { split($i,a,":"); printf(", "a[2]); } printf("\n"); }' > letor.data
之後,將看到 'letor.data' 如下
doc_244338, 1.000000, 1.000000, 0.833333, 0.871264, 0, 0, 0, 0.941842, 1.000000, 1.000000, 1.000000, 1.000000, 1.000000, 1.000000, 1.000000, 1.000000, 1.000000, 0.719697, 0.729351, 0, 0, 0, 0.811565, 1.000000, 0.972730, 1.000000, 1.000000, 0.922374, 0.946654, 0.938888, 1.000000, 1.000000, 0.711276, 0.722202, 0, 0, 0, 0.798002, 1.000000, 1.000000, 1.000000, 1.000000, 0.959134, 0.963919, 0.971425
現在,可以將 'letor.data' 檔案載入到 R 中,並執行 PCA 將文件繪製在二維空間中,如下所示
data=read.table("letor.data",sep=",")
summary(pc.cr <- princomp(data[,2:46]))
loadings(pc.cr)
library(lattice)
pc.cr$scores
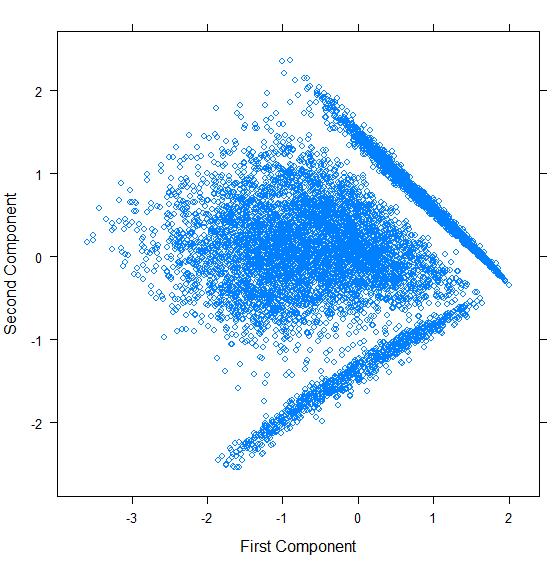
pca.plot <- xyplot(pc.cr$scores[,2] ~ pc.cr$scores[,1])
pca.plot$xlab <- "First Component"
pca.plot$ylab <- "Second Component"
pca.plot
上面的指令碼生成以下圖表
正如我們所見,儘管文件由多個特徵(>45)表示,但 PCA 能夠找到 2 個主成分,這些成分被用於在二維圖表中繪製所有文件。