R 中的資料探勘演算法/頻繁模式挖掘/FP-Growth 演算法

在資料探勘中，尋找大型資料庫中的頻繁模式的任務非常重要，並在過去幾年中被大規模研究。不幸的是，這項任務計算量很大，尤其是在存在大量模式的情況下。

FP-Growth 演算法由 Han 在 中提出，是一種高效且可擴充套件的方法，它透過模式片段增長來挖掘完整的頻繁模式集，並使用擴充套件的字首樹結構來儲存關於頻繁模式的壓縮和關鍵資訊，稱為頻繁模式樹（FP-Tree）。在他的研究中，Han 證明了他的方法優於其他流行的挖掘頻繁模式的方法，例如 Apriori 演算法 和 TreeProjection 。在一些後續作品 中證明，FP-Growth 具有比其他方法更好的效能，包括 Eclat 和 Relim 。FP-Growth 演算法的普及和效率促成了許多研究，這些研究提出了改進其效能的變體 。

本章介紹了該演算法和一些變體，並討論了 R 語言的特性以及在 R 中實現該演算法以供使用的策略。接下來，提出了簡要的結論和未來工作。

該演算法

FP-Growth 演算法是一種尋找頻繁項集的替代方法，無需使用候選生成，從而提高效能。為此，它使用分治策略 。該方法的核心是使用一種稱為頻繁模式樹（FP-Tree）的特殊資料結構，它保留了項集關聯資訊。

簡單來說，該演算法的工作原理如下：首先，它壓縮輸入資料庫，建立 FP-Tree 例項來表示頻繁項。完成第一步後，它將壓縮後的資料庫劃分為一組條件資料庫，每個資料庫都與一個頻繁模式相關聯。最後，分別挖掘每個這樣的資料庫。使用這種策略，FP-Growth 減少了遞迴查詢短模式的搜尋成本，然後將它們連線成長頻繁模式，提供了良好的選擇性。

在大型資料庫中，不可能將 FP-Tree 儲存在主記憶體中。解決此問題的策略是首先將資料庫劃分為一組較小的資料庫（稱為投影資料庫），然後從每個較小的資料庫構建 FP-Tree。

接下來的幾個小節將描述 FP-Tree 結構和 FP-Growth 演算法，最後將提供一個示例，以便更輕鬆地理解這些概念。

FP-Tree 結構

頻繁模式樹（FP-Tree）是一種緊湊的結構，用於儲存資料庫中頻繁模式的定量資訊 。

Han 將 FP-Tree 定義為如下所示的樹結構

1. 一個標記為“null”的根，其子節點是一組項字首子樹；
2. 項字首子樹中的每個節點都包含三個欄位

1. 項名稱：註冊節點表示的項；
2. 計數：到達節點的路徑部分所表示的事務數量；
3. 節點連結：連結到 FP-Tree 中下一個具有相同項名稱的節點，如果不存在則為 null。

1. 頻繁項表頭表中的每個條目都包含兩個欄位

1. 項名稱：與節點相同；
2. 節點連結頭部：指向 FP-Tree 中第一個攜帶該項名稱的節點的指標。

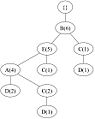
此外，頻繁項表頭表可以包含項的計數支援。下面的圖 1 展示了一個 FP-Tree 的示例。

• 

圖 1：來自 的 FP-Tree 示例。

Han 在 中定義的構建 FP-Tree 的原始演算法如下所示，即演算法 1。

演算法 1：FP-Tree 構建

輸入：事務資料庫 DB 和最小支援閾值 ?。

輸出：FP-Tree，DB 的頻繁模式樹。

方法：FP-Tree 按以下步驟構建。

1. 掃描事務資料庫 DB 一次。收集 F，即頻繁項集，以及每個頻繁項的支援度。按支援度降序對 F 進行排序，得到 FList，即頻繁項列表。
2. 建立 FP-Tree T 的根，並將其標記為“null”。對於 DB 中的每個事務 Trans，執行以下操作

• 選擇 Trans 中的頻繁項，並根據 FList 的順序對它們進行排序。令 Trans 中排序後的頻繁項列表為 [ p | P]，其中 p 是第一個元素，P 是其餘列表。呼叫 insert tree([ p | P], T )。
• 函式 insert tree([ p | P], T ) 的執行方式如下。如果 T 存在子節點 N，使得 N.item-name = p.item-name，則將 N 的計數加 1；否則，建立一個新節點 N，其計數初始化為 1，其父連結指向 T，其節點連結透過節點連結結構指向具有相同項名稱的節點。如果 P 不為空，則遞迴呼叫 insert tree(P, N )。

使用此演算法，FP-Tree 在掃描資料庫兩次後構建完成。第一次掃描收集並排序頻繁項集，第二次掃描構建 FP-Tree。

FP-Growth 演算法

構建完 FP-Tree 後，就可以對其進行挖掘，以找到完整的頻繁模式集。為了完成這項工作，Han 在 中提出了一組引理和性質，之後描述了 FP-Growth 演算法，如下所示，即演算法 2。

演算法 2：FP-Growth

輸入：一個數據庫 DB，由根據演算法 1 構建的 FP-Tree 表示，以及最小支援閾值 ?。

輸出：完整的頻繁模式集。

方法：呼叫 FP-growth(FP-tree, null)。

過程 FP-growth(Tree, a) {

(01) 如果 Tree 包含一條字首路徑，則 { // 挖掘單字首路徑 FP-Tree

(02) 令 P 為 Tree 的單字首路徑部分；

(03) 令 Q 為多路徑部分，其中頂部分支節點被替換為 null 根；

(04) 對於路徑 P 中節點的每個組合（記為 ß），執行以下操作

(05) 生成模式 ß ∪ a，其支援度 = ß 中節點的最小支援度；

(06) 令 freq pattern set(P) 為如此生成的模式集；

}

(07) 否則，令 Q 為 Tree；

(08) 對於 Q 中的每個項 ai，執行以下操作 { // 挖掘多路徑 FP-Tree

(09) 生成模式 ß = ai ∪ a，其支援度 = ai .support；

(10) 構建 ß 的條件模式庫，然後構建 ß 的條件 FP-Tree Tree ß；

(11) 如果 Tree ß ≠ Ø，則

(12) 呼叫 FP-growth(Tree ß , ß)；

(13) 令 freq pattern set(Q) 為如此生成的模式集；

}

(14) 返回 (freq pattern set(P) ∪ freq pattern set(Q) ∪ (freq pattern set(P) × freq pattern set(Q)))

}

當 FP 樹包含單個字首路徑時，可以將完整的頻繁模式集劃分為三個部分生成：單個字首路徑 P、多路徑 Q 以及它們的組合（第 01 到 03 行和第 14 行）。單個字首路徑的所得模式是其具有最小支援的子路徑的列舉（第 04 到 06 行）。之後，定義多路徑 Q（第 03 或 07 行）並處理由此產生的模式（第 08 到 13 行）。最後，在第 14 行，將組合的結果作為找到的頻繁模式返回。

一個例子

本節提供一個簡單的示例來說明先前演算法的工作原理。原始示例可以在 中檢視。

考慮以下交易，最小支援度為 3

	i(t)
1	FBAED
2	BCE
3	ABDE
4	ABCE
5	ABCDE
6	BCD

要構建 FP 樹，首先計算頻繁項的支援度並按降序排列，得到以下列表：{ B(6), E(5), A(4), C(4), D(4) }。然後，使用排序後的專案列表，如 圖 2 所示，為每個交易迭代地構建 FP 樹。

• 
  (a) 交易 1：BEAD
• 
  (b) 交易 2：BEC
• 
  (c) 交易 3：BEAD
• 
  (d) 交易 4：BEAC
• 
  (e) 交易 5：BEACD
• 
  (f) 交易 6：BCD

圖 2：迭代構建 FP 樹。

如圖 3 所示，對 FP-Growth 的初始呼叫使用從演算法 1 獲得的 FP 樹（如 圖 2 (f) 所示），以在對投影樹進行遞迴呼叫時處理之前提供的交易中的頻繁模式。

使用深度優先策略，分別確定到專案 D、C、A、E 和 B 的投影樹。首先遞迴處理 D 的投影樹，投影 DA、DE 和 DB 的樹。以類似的方式處理剩餘的專案。在處理結束時，頻繁項集為：{ DAE, DAEB, DAB, DEB, DA, DE, DB, CE, CEB, CB, AE, AEB, AB, EB }。

圖 3：FP-Growth 演算法遞迴呼叫發現的投影樹和頻繁模式。

FP-Growth 演算法變體

如前所述，FP-Growth 演算法的流行和效率促成了許多研究，這些研究提出了各種變體來提高其效能 。本節簡要介紹其中一些。

DynFP-Growth 演算法

DynFP-Growth ，重點關注基於兩個觀察到的問題的 FP-Tree 演算法構建的改進

1. 對於相同的“邏輯”資料庫，生成的 FP 樹並不唯一；
2. 該過程需要對資料庫進行兩次完整掃描。

為了解決第一個問題，Gyorödi C. 等人 提出了使用支援降序排列以及詞典排序的方法，從而確保了對於不同的“邏輯上等效”資料庫，生成的 FP 樹的唯一性。為了解決第二個問題，他們建議設計一種動態 FP 樹重排序演算法，並在檢測到至少一項提升到更高階時使用此演算法。

此方法的一個重要特點是，當實際資料庫更新時，無需重建 FP 樹。只需再次執行演算法，並考慮新交易和儲存的 FP 樹。

由於動態重排序過程，另一個提議的適應性是在原始結構中的修改，用雙向連結串列替換單向連結串列以將樹節點連結到標題，並在同一標題中新增一個主表。有關更多詳細資訊，請參閱 。

FP-Bonsai 演算法

FP-Bonsai 透過使用 ExAnte 資料減少技術 減少（修剪）FP 樹來提高 FP-Growth 效能。修剪後的 FP 樹稱為 FP-Bonsai。有關更多詳細資訊，請參閱 。

AFOPT 演算法

Liu 在 中提出了 AFOPT 演算法，該演算法旨在從四個方面提高 FP-Growth 演算法的效能

• 專案搜尋順序：當搜尋空間被劃分時，所有專案都按某種順序排序。使用不同的專案搜尋順序，構造的條件資料庫的數量可能會有很大差異；
• 條件資料庫表示：條件資料庫的遍歷和構造成本在很大程度上取決於其表示；
• 條件資料庫構建策略：物理地構建每個條件資料庫可能很昂貴，會影響每個單獨條件資料庫的挖掘成本；
• 樹遍歷策略：使用自上而下的遍歷策略，樹的遍歷成本最小。

有關更多詳細資訊，請參閱 。

NONORDFP 演算法

Nonordfp 演算法 的靈感來自 FP-Growth 演算法的執行時間和空間需求。理論上的區別是主要資料結構（FP 樹），它更緊湊，並且不需要在每個條件步驟中重建它。引入了使用 Trie 資料結構 的 FP 樹的緊湊、記憶體高效表示，其記憶體佈局允許更快的遍歷、更快的分配以及可選的投影。有關更多詳細資訊，請參閱 。

FP-Growth* 演算法

該演算法由 Grahne 等人提出。^[16][19]，並基於他對使用 FP-Growth 計算頻繁項集的 CPU 時間的結論。他們觀察到 80% 的 CPU 時間用於遍歷 FP-Tree。^[9] 因此，他們使用基於陣列的資料結構結合 FP-Tree 資料結構來減少遍歷時間，並結合了幾種最佳化技術。有關詳細資訊，請參見^[16][19]。

PPV、PrePost 和 FIN 演算法

這三種演算法由 Deng 等人提出。^[20][21][22]，並基於三種新穎的資料結構，即節點列表^[20]、N-列表^[21] 和節點集^[22]，分別用於促進頻繁項集的挖掘過程。它們基於 FP-Tree，每個節點都用前序遍歷和後序遍歷進行編碼。與節點列表相比，N-列表和節點集更高效。這使得 PrePost ^[21] 和 FIN ^[22] 的效率高於 PPV ^[20]。有關詳細資訊，請參見^[20][21][22]。

R 中的資料視覺化

通常，用於挖掘頻繁項集的資料儲存在文字檔案中。視覺化資料的第一步是將其載入到資料幀中（一個表示 R 中資料的物件）。

函式 read.table 可以以以下方式使用

var <- read.table(fileName, fileEncoding=value, header = value, sep = value)

Where:
  • var: the R variable to receive the loaded data.
  • fileName: is a string value with the name of the file to be loaded.
  • fileEncoding: to be used when the file has no-ASCII characters.
  • header: indicates that the file has headers (T or TRUE) or not (F or FALSE).
  • sep: defines the field separator character (“,”, “;” or “\t” for example)
  • Only the filename is a mandatory parameter.

R 中另一個用於載入資料的函式稱為 scan。有關詳細資訊，請參見 R 資料匯入/匯出手冊。

資料的視覺化可以透過兩種方式完成

• 使用變數名 (var) 以表格形式列出資料。
• 以及 summary(var) 以列出資料的摘要。

示例

> data <- read.table("boolean.data", sep=",", header=T)

> data
      A    B     C     D     E
1  TRUE TRUE FALSE  TRUE  TRUE
2 FALSE TRUE  TRUE FALSE  TRUE
3  TRUE TRUE FALSE  TRUE  TRUE
4  TRUE TRUE  TRUE FALSE  TRUE
5  TRUE TRUE  TRUE  TRUE  TRUE
6 FALSE TRUE  TRUE  TRUE FALSE

> summary(data)
     A              B               C               D               E
 Mode :logical   Mode:logical   Mode :logical   Mode :logical   Mode :logical
 FALSE:2         TRUE:6         FALSE:2         FALSE:2         FALSE:1
 TRUE :4         NA's:0         TRUE :4         TRUE :4         TRUE :5
 NA's :0                        NA's :0         NA's :0         NA's :0

在上面的示例中，使用簡單的二進位制資料庫“boolean.data”中的資料載入到資料幀變數 data 中。在命令列中鍵入變數名，將列印其內容，鍵入 summary 命令將列印每個專案的頻率出現情況。summary 函式的工作方式不同。它取決於變數中資料的型別，有關詳細資訊，請參見^[23][24][25]。

之前介紹的函式可能很有用，但對於頻繁項集資料集，使用一個名為 arules ^[26] 的特定包可以更好地視覺化資料。

使用 arules，提供了一些函式

• read.transactions：用於將資料庫檔案載入到變數中。
• inspect：用於列出事務。
• length：返回事務數量。
• image：繪製包含所有事務的矩陣格式的影像。
• itemFrequencyPlot：計算每個專案的頻率並將其繪製在條形圖中。

示例

> data <- read.transactions("basket.data", format="basket", sep = ",")

> data
transactions in sparse format with
 6 transactions (rows) and
 5 items (columns)

> inspect(data)
  items
1 {A,
   B,
   D,
   E}
2 {B,
   C,
   E}
3 {A,
   B,
   D,
   E}
4 {A,
   B,
   C,
   E}
5 {A,
   B,
   C,
   D,
   E}
6 {B,
   C,
   D}

> length(data)
[1] 6

> image(data)

> itemFrequencyPlot(data, support=0.1)

在這個例子中，我們可以看到在命令列中使用變數名的區別。從事務中，只打印了行數（事務）和列數（專案）。image(data) 和 itemFrequencyPlot(data, support = 0.1) 的結果分別在下面的圖 4 和圖 5 中給出。

• 

圖 4：image(data) 呼叫的結果。

• 

圖 5：itemFrequencyPlot(data, support = 0.1) 呼叫的結果。

R 中的實現

R ^{[23][24][25][27][28]} 提供了用於資料操作、計算和圖形顯示的幾種工具，非常適用於資料分析和挖掘。它既可以用作統計庫，也可以用作程式語言。

作為統計庫，它提供了一組用於彙總資料、矩陣工具、機率分佈、統計模型和圖形過程的函式。

作為程式語言，它提供了一組函式、命令和方法來例項化和管理不同型別物件的的值（包括列表、向量和矩陣）、使用者互動（從控制檯輸入和輸出）、控制語句（條件語句和迴圈語句）、函式的建立、對外部資源的呼叫以及建立包。

本章並沒有完成對 R 資源的詳細介紹，而是重點關注使用 R 實現演算法或在 R 中使用的挑戰。但是，為了更好地理解 R 的功能，在附錄 A 中提供了一些基於^[28] 的基本示例。

使用 R 實現演算法通常需要建立複雜的物件來表示要處理的資料結構。此外，可能需要實現複雜函式來處理這些資料結構。考慮到使用 R 實現 FP-Growth 演算法的具體情況，僅使用 R 資源可能很難表示和處理 FPTree。此外，出於效能原因，使用其他語言實現演算法並將其與 R 整合可能很有趣。使用其他語言的其他原因是獲得更好的記憶體管理以及使用現有的包^[29]。

有兩種方法可以將 R 與其他語言整合，下面將簡要介紹：建立包和使用介面函式進行外部呼叫。^[24] 接下來介紹了在這項工作中使用的 FP-Growth 實現以及將其與 R 整合的努力。對於兩者，都需要安裝 RTools。

建立包

包是將用其他語言實現的可選程式碼載入到 R 中的一種機制。^[24] R 發行版本身包含大約 25 個包，本 WikiBook 中使用的一些額外包可以列出

• aRules
• arulesNBMiner
• arulesSequences
• cluster

要建立包，需要遵循一些規範。R 包的來源包含在下面描述的目錄結構中

• 根目錄：包含 DESCRIPTION 檔案和一些可選檔案（INDEX、NAMESPACE、configure、cleanup、LICENCE、COPYING 和 NEWS）的根目錄。
• R：僅包含 R 程式碼檔案，這些檔案可以透過 R 命令 source(filename) 執行以建立使用者使用的 R 物件。或者，此目錄可以包含一個檔案 sysdata.rda。此檔案包含在 R 控制檯執行中建立的 R 物件的儲存影像。
• data：旨在包含資料檔案，這些檔案可以透過延遲載入提供或使用函式 data() 載入。這些資料檔案可以來自三種不同型別：純 R 程式碼（.r 或 .R）、表格（.tab、.txt 或 .csv）或來自 R 控制檯的儲存資料（.RData 或 .rda）。一些額外的壓縮檔案可用於表格檔案。
• demo：包含純 R 程式碼中的指令碼（用於使用函式 demo() 執行），這些指令碼演示了包中的一些功能。
• exec：可能包含包需要的其他可執行檔案，通常是用於 shell、Perl 或 Tcl 等直譯器的指令碼。
• inst：其內容將在構建後複製到安裝目錄，其 Makefile 可以建立要安裝的檔案。可能包含所有旨在供終端使用者檢視的資訊檔案。
• man：應僅包含包中物件的文件檔案（使用特定的 R 文件格式）。空 man 目錄會導致安裝錯誤。
• po：用於與國際化相關的檔案，換句話說，用於翻譯錯誤和警告訊息。
• src：包含原始碼、標頭檔案、makevars 和 makefile。支援的語言有：C、C++、FORTRAN 77、Fortran 9x、Objective C 和 Objective C++。在一個包中混合所有這些語言是不可能的，但混合 C 和 FORTRAN 77 或 C 和 C++ 似乎很成功。但是，有一些方法可以從其他包中進行使用。
• tests：用於其他特定於包的測試程式碼。

建立原始碼包後，必須在作業系統控制檯的命令列中安裝它。

R CMD INSTALL <parameters>

或者，可以使用 R 控制檯中的命令列從 R 中下載並安裝包。

> install.packages(<parameters>)

請參閱 安裝和管理手冊 ，瞭解詳細資訊。

安裝後，需要使用 R 控制檯中的命令列載入包才能使用它。

> library(packageName)

使用介面函式進行外部呼叫

使用介面函式進行外部呼叫是一種簡單的方法，可以無需遵守之前描述的所有規則來建立 R 包，即可使用外部實現。

首先，程式碼需要包含 R.h 標頭檔案，該檔案隨 R 安裝一起提供。

要編譯原始碼，需要在作業系統命令列中使用 R 編譯器。

> R CMD SHLIB <parameters>

要用於 R 的編譯程式碼需要在類 Unix 作業系統中作為共享物件載入，或在 Windows 作業系統中作為 DLL 載入。要載入或解除安裝它，可以使用 R 控制檯中的命令。

> dyn.load(fileName)
> dyn.unload(fileName)

載入後，可以使用以下函式之一呼叫外部程式碼。

• .C
• .Call
• .Fortran
• .External

下面展示了兩個簡單的示例，使用 .C 函式。

示例 1：Hello World

## C code in file example1.c

#include <R.h>

Void do_stuff ()
{
   printf("\nHello, I'm in a C code!\n");
}


## R code in file example.R

dyn.load("example1.dll")

doStuff <-
function (){
    tmp <- .C("do_stuff")
	rm(tmp)
	return(0)
}

doStuff()


## Compiling code in OS command line

C:\R\examples>R CMD SHLIB example1.c
gcc -I"C:/PROGRA~1/R/R-212~1.0/include" -O3 -Wall -std=gnu99 -c example1.c -o example1.o
gcc -shared -s -static-libgcc -o example1.dll tmp.def example1.o -LC:/PROGRA~1/R/R-212~1.0/bin/i386 -lR


## Output in R console

> source("example1.R")

Hello, I'm in a C code!
>

示例 2：使用整數向量呼叫 C

##C code in file example2.c

#include <R.h>

void doStuff(int *i) {
    i[0] = 11;
}


## Output in R console

> dyn.load("example2.dll")
> a <- 1:10
> a
 [1]  1  2  3  4  5  6  7  8  9 10
> out <- .C("doStuff", b = as.integer(a))
> a
 [1]  1  2  3  4  5  6  7  8  9 10
> out$b
 [1] 11  2  3  4  5  6  7  8  9 10

FP-Growth 實現

此工作中使用的 FP-Growth 實現由 Christian Borgelt 實現，他是歐洲軟計算中心的首席研究員。他還實現了 arules 包 中用於 Eclat 和 Apriori 演算法的程式碼。原始碼可以從他的個人網站下載。

正如 Borgelt 所描述的那樣，核心操作的實現變體（計算 FP 樹的投影）有兩種。此外，投影的 FP 樹可以選擇透過刪除變得不再頻繁的項來進行修剪（使用 FP-Bonsai 方法）。

原始碼分為三個主要資料夾（包）。

• fpgrowth：包含實現演算法並管理 FP 樹的主要檔案；
• tract：管理項集、事務及其報告；
• util：用於 fpgrowth 和 tract 的工具。

從作業系統命令列呼叫此實現的語法為

> fpgrowth [options] infile [outfile [selfile]]
-t#      target type                              (default: s)
         (s: frequent, c: closed, m: maximal item sets,
          g: generators, r: association rules)
-m#      minimum number of items per set/rule     (default: 1)
-n#      maximum number of items per set/rule     (default: no limit)
-s#      minimum support of an item set/rule      (default: 10%)
-S#      maximum support of an item set/rule      (default: 100%)
         (positive: percentage, negative: absolute number)
-o       use original rule support definition     (body & head)
-c#      minimum confidence of an assoc. rule     (default: 80%)
-e#      additional evaluation measure            (default: none)
-a#      aggregation mode for evaluation measure  (default: none)
-d#      threshold for add. evaluation measure    (default: 10%)
-i       invalidate eval. below expected support  (default: evaluate all)
-p#      (min. size for) pruning with evaluation  (default: no pruning)
         (< 0: weak forward, > 0 strong forward, = 0: backward pruning)
-q#      sort items w.r.t. their frequency        (default: 2)
         (1: ascending, -1: descending, 0: do not sort,
          2: ascending, -2: descending w.r.t. transaction size sum)
-A#      variant of the fpgrowth algorithm to use (default: c)
-x       do not prune with perfect extensions     (default: prune)
-l#      number of items for k-items machine      (default: 16)
         (only for variants s and d, options -As or -Ad)
-j       do not sort items w.r.t. cond. support   (default: sort)
         (only for algorithm variant c, option -Ac)
-u       do not use head union tail (hut) pruning (default: use hut)
         (only for maximal item sets, option -tm)
-F#:#..  support border for filtering item sets   (default: none)
         (list of minimum support values, one per item set size,
         starting at the minimum size, as given with option -m#)
-R#      read item selection/appearance indicators
-P#      write a pattern spectrum to a file
-Z       print item set statistics (number of item sets per size)
-N       do not pre-format some integer numbers   (default: do)
-g       write item names in scanable form (quote certain characters)
-h#      record header  for output                (default: "")
-k#      item separator for output                (default: " ")
-I#      implication sign for association rules   (default: " <- ")
-v#      output format for set/rule information   (default: " (%S)")
-w       integer transaction weight in last field (default: only items)
-r#      record/transaction separators            (default: "\n")
-f#      field /item        separators            (default: " \t,")
-b#      blank   characters                       (default: " \t\r")
-C#      comment characters                       (default: "#")
-!       print additional option information
infile   file to read transactions from           [required]
outfile  file to write item sets/assoc. rules to  [optional]

可以選擇每個集合的項數限制、最小支援度、評估度量、配置輸入和輸出格式等等。

使用 test1.tab 示例檔案（隨原始碼提供）作為輸入檔案、test1.out 和最小支援度為 30% 對 FP-Growth 進行簡單呼叫，其結果如下所示。

C:\R\exec\fpgrowth\src>fpgrowth -s30 test1.tab test1.out
fpgrowth - find frequent item sets with the fpgrowth algorithm
version 4.10 (2010.10.27)        (c) 2004-2010   Christian Borgelt
reading test1.tab ... [5 item(s), 10 transaction(s)] done [0.00s].
filtering, sorting and recoding items ... [5 item(s)] done [0.00s].
reducing transactions ... [8/10 transaction(s)] done [0.00s].
writing test1.out ... [15 set(s)] done [0.00s].

結果顯示了一些關於版權的資訊和一些執行資料，例如項數、事務數和頻繁集數（本例中為 21 個）。輸入和輸出檔案的內容如下所示。

輸入檔案內容

a b c
a d e
b c d
a b c d
b c
a b d
d e
a b c d
c d e
a b c

輸出檔案內容

e d  (30.0)
e  (30.0)
a c b  (40.0)
a c  (40.0)
a d b  (30.0)
a d  (40.0)
a b  (50.0)
a  (60.0)
d b c  (30.0)
d b  (40.0)
d c  (40.0)
d  (70.0)
c b  (60.0)
c  (70.0)
b  (70.0)

從 R 呼叫 FP-Growth

如前所述，要建立一個包，需要遵守幾個規則，建立標準目錄結構和內容，以使外部原始碼可用。前面介紹了另一種方法，即建立共享物件或 DLL，並使用特定的 R 函式（.C、.CALL 等等）呼叫它。

從頭開始做將現有程式碼改編成一個包的工作可能是一項艱鉅的任務，需要花費大量時間。一個有趣的方法是迭代地建立和改編共享物件或 DLL，並進行測試以驗證它，並在一些迭代後改進改編，當獲得滿意的結果後，開始進行包版本的工作。

使 C 實現可用於 R 的迭代意圖如下所示。

1. 建立一個簡單的命令列呼叫，不帶引數，只對原始原始碼（fpgrowth.c 檔案）進行兩個更改。

• 將主函式重新命名為 FP-Growth，並使用相同的簽名；
• 建立一個要從 R 中呼叫的函式，從配置檔案建立引數（僅包含一個與命令列語法相同的字串，將其分解成一個數組，以用作 FP-Growth 函式的引數陣列）；

2. 使用 R 編譯命令編譯程式碼專案，包括 R.h 讀取器檔案，並使用 R 呼叫它；

3. 實施來自 R 呼叫的輸入引數，消除配置檔案的使用，包括更改以定義輸入檔名以用於 R 中的資料幀；

4. 將輸出準備成一個 R 資料幀，以返回到 R；

5. 建立 R 包。

第一次迭代可以輕鬆完成，沒有任何意外。

不幸的是，第二次迭代看起來也很容易完成，但在實踐中卻證明非常困難。R 編譯命令不能與 makefile 一起使用，因此無法使用它來編譯原始程式碼。經過一些實驗後，策略改為使用改編後的程式碼構建一個庫，沒有建立要從 R 中呼叫的函式，然後建立一個包含此函式並使用編譯後的庫的新程式碼。接下來，從 R 呼叫新編譯的 DLL 會引發執行錯誤。在除錯執行過程中，浪費了大量時間，發現建立庫的一些編譯配置是錯誤的。為了解決這個問題，進行了一些測試，建立了一個可執行版本，使用作業系統命令列執行它，直到所有執行錯誤都得到解決。然而，解決了這些錯誤後，又發現了另一個意外的行為。從 R 控制檯呼叫使用 R 命令編譯的版本，在載入 DLL 函式時，出現了 cygwin 版本不相容的錯誤。嘗試了很多實驗，更改編譯引數、cygwin 的不同版本等等，但都沒有成功（這些測試只在 Windows 作業系統下進行）。因此，在第二次迭代中沒有取得成功，後面的步驟就變得很困難。

第三和第四次迭代中預期的主要挑戰是將 R 資料型別和結構與其在 C 語言中的對應物進行介面，無論是用於資料集輸入和要轉換為內部使用的其他輸入引數，還是用於建立要返回到 R 的輸出資料集。另一種方法是改編所有程式碼以使用接收到的資料。但是，這似乎更復雜。

第五次迭代看起來像是一項官僚工作。一旦程式碼完全改編並驗證，建立額外的目錄和所需內容應該是一件容易的事。

結論和未來工作

本章介紹了一種用於挖掘資料庫中頻繁模式的有效且可擴充套件的演算法：FP-Growth。該演算法使用了一種有用的資料結構 FP 樹來儲存關於頻繁模式的資訊。還介紹了該演算法的實現。此外，還介紹了 R 語言的一些特性以及將演算法原始碼改編以在 R 中使用的實驗。我們可以觀察到，進行這種改編是一項艱鉅的任務，無法在短時間內完成。不幸的是，還沒有時間來完成這種改編。

作為一項未來工作，將對更好地理解 R 中外部資源的實現以及完成本工作中提出的任務，並在隨後將結果與 R 中可用的其他頻繁項集挖掘演算法進行比較，會很有趣。

附錄 A：R 語句示例

一些基於 的基本示例。

獲取有關函式的幫助

> help(summary)
> ?summary

建立物件

> perceptual <- 1.2

數字表達式

> z <- 5
> w <- z^2
> y <- (34 + 90) / 12.5

列印物件值

> w
[1] 25

建立向量

> v <- c(4, 7, 23.5, 76.2, 80)

向量運算

> x <- sqrt(v)
> v1<- c(4, 6, 87)
> v2 <- c(34, 32.4, 12)
> v1 + v2
[1] 38.0 38.4 99.0

分類資料

> s <- c("f", "m", "m", "f")
> s
[1] "f" "m" "m" "f"
> s <- factor(s)
> s
[1] f m m f
Levels: f m
> table(s)
s
f m
2 2

序列

> x <- 1:1000
> y <- 5:0
> z <- seq(-4, 1, 0.5) # create a sequence starting in -4, stopping in 1 
                       # with an increment of 0.5
> w <- rnorm(10) # create a random sequence of 10 numeric values
> w <- rnorm(10, mean = 10, sd = 3) # create a normal distribution of 
                                    # 10 numeric values with mean of 10
                                    # and standard deviation of 3

矩陣

> m1 <- matrix(c(45,  23,  66,  77,  33,  44),  2,  3)
> m1
        [,1]   [,2]   [,3]
[1,]     45     66     33
[2,]     23     77     44
> m2 <- matrix(c(12,  65,  32,  7,  4,  78),  2,  3)
> m2
        [,1]   [,2]   [,3]
[1,]     12     32      4
[2,]     65      7     78
> m1 + m2
        [,1]   [,2]   [,3]
[1,]     57     98     37
[2,]     88     84    122

列表

> student <- list(nro = 34453, name = "Marie", scores = c(9.8, 5.7, 8.3))
> student[[1]]
[1] 34353
> student$nro
[1] 34353

資料框（表示資料庫表格）

> scores.inform <- data.frame(nro = c(2355, 3456, 2334, 5456),
+ team = c("tp1", "tp1", "tp2", "tp3"), 
+ score = c(10.3, 9.3, 14.2, 15))
> scores.inform
    nro    team   score
1  2355     tp1    10.3
2  3456     tp1     9.3
3  2334     tp2    14.2
4  5456     tp3    15.0
> scores.inform[score > 14,]
    nro    team   score
3  2334     tp2    14.2
4  5456     tp3    15.0
> team
[1]  tp1  tp1  tp2  tp3
Levels:  tp1  tp2  tp3

條件語句

> if (x > 0) y <- z / x else y <- z
> if (x > 0) {
+    cat('x is positive.\n')
+    y <- z / x
+} else {
+    cat('x isn't positive!\n')
+    y <- z
+}

case 語句

> sem <- "green"
> switch(sem, green = "continue", yellow = "attention", red = "stop")
[1] "continue"

迴圈語句

> x <- rnorm(1)
> while (x < -0.3) {
+    cat("x=", x, "\t")
+    x <- rnorm(1)
+  }

> text  <-  c()
> repeat  {
+   cat('Type a phrase?  (empty to quit) ')
+   fr  <-  readLines(n=1)
+   if  (fr  ==  '')  break  else  texto  <-  c(texto,fr)
+}

> x <- rnorm(10)
> k <- 0
> for(v in x)  {
+   if(v > 0)
+     y <- v
+   else y <- 0
+     k <- k + y
+  }

建立和呼叫函式

> cel2far <- function(cel) {
+   res  <-  9/5  *  cel  +  32
+   res
+ }
> cel2far(27.4)
[1]  81.32
> cel2far(c(0,  -34.2,  35.6,  43.2))
[1]  32.00  -29.56    96.08  109.76