密度泛函理論/Hartree–Fock 方法

Hartree-Fock (HF) 或自洽場 (SCF)

在 計算物理學 和 化學 中，Hartree–Fock (HF) 方法是一種近似方法，用於確定 波函式 和 量子多體系統 在 穩態 中的能量。

Hartree–Fock 方法通常假設系統的精確的，N 體波函式可以用單個 Slater 行列式（當粒子是 費米子 時）或單個 永久行列式（當粒子是 玻色子 時）來近似，這兩個行列式分別由 N 個 自旋軌道 組成。 透過呼叫 w:變分法，可以推匯出 N 個自旋軌道的 N 個耦合方程組。 這些方程組的解將給出系統的 Hartree–Fock 波函式和能量。

特別是在較早的文獻中，Hartree–Fock 方法也被稱為自洽場方法 (SCF)。 在推匯出現在被稱為 Hartree 方程 的 薛定諤方程 的近似解時，哈特里 要求從電荷分佈計算出的最終場與假設的初始場“自洽”。 因此，自洽是解的一個要求。 非線性 Hartree–Fock 方程的解表現得好像每個粒子都受到所有其他粒子產生的平均場的約束（參見下面 Fock 算符），因此術語得以延續。 這些方程幾乎普遍透過 迭代法 求解，儘管 不動點迭代 演算法並不總是收斂。^[1] 這種求解方案並非唯一可能的方案，也並非 Hartree–Fock 方法的本質特徵。

Hartree–Fock 方法通常應用於求解原子、分子、奈米結構^[2] 和固體的 薛定諤方程，但它也廣泛應用於 核物理學 中。 （參見 Hartree–Fock–Bogoliubov 方法，瞭解其在 核結構 理論中的應用）。 在 原子結構 理論中，計算可能是針對具有許多激發能級的譜線，因此 Hartree–Fock 原子方法 假設波函式是具有明確 量子數 的單個 組態態函式，並且能級並不一定是 基態。

對於原子和分子，Hartree–Fock 解是大多數更準確地描述多電子系統的方案的中心起點。

本文的其餘部分將重點介紹適用於具有原子作為特例的分子 的電子結構理論中的應用。 這裡的討論僅針對限制性 Hartree–Fock 方法，其中原子或分子是閉殼層系統，所有軌道（原子或分子）都是雙佔據的。 開殼 系統，其中一些電子沒有配對，可以透過兩種 Hartree–Fock 方法之一處理

• w:限制性開殼 Hartree–Fock (ROHF)
• w:無限制 Hartree–Fock (UHF)

歷史

Hartree–Fock 方法的起源可以追溯到 20 世紀 20 年代末，當時距 1926 年發現 w:薛定諤方程 只有幾年時間。 1927 年，D. R. 哈特里 提出了一種程式，他稱之為自洽場方法，用於計算原子和離子的近似波函式和能量。 哈特里的靈感來自於 20 世紀 20 年代初的一些早期的半經驗方法（由 E. Fues、R. B. 林賽 和他自己提出），這些方法被設定在玻爾的 w:舊量子論 框架中。

在w:玻爾模型中，具有w:主量子數 n 的狀態的能量以原子單位表示為 $E=-1/n^{2}$。從原子光譜中觀察到，多電子原子的能級可以透過應用玻爾公式的修正版本來很好地描述。透過引入w:量子虧損 *d* 作為經驗引數，通用原子的能級可以用公式$E=-1/(n+d)^{2}$很好地近似，從這個意義上說，可以相當好地重現觀察到的w:X射線區域的躍遷能級（例如，參見w:莫塞萊定律中的經驗討論和推導）。非零量子虧損的存在歸因於電子-電子排斥，這種排斥在孤立的氫原子中顯然不存在。這種排斥導致了裸核電荷的區域性遮蔽。這些早期的研究人員後來引入了包含其他經驗引數的其他勢，希望更好地重現實驗資料。

哈特里試圖消除經驗引數，並從基本的物理原理，即從頭算，來求解多體時間無關薛定諤方程。他提出的第一個求解方法被稱為哈特里方法。然而，哈特里的許多同時代人並不理解哈特里方法背後的物理推理：它在許多人看來包含經驗元素，其與多體薛定諤方程解的聯絡也不清楚。然而，在 1928 年，J. C. 斯萊特 和 J. A. 岡特獨立地證明，哈特里方法可以透過將w:變分原理應用於w:試探波函式（作為單粒子函式的乘積）來建立在更合理的理論基礎上。

1930 年，斯萊特和V. A. 福克 獨立地指出，哈特里方法不尊重波函式的反對稱性原理。哈特里方法使用w:泡利不相容原理的舊形式，禁止兩個電子處於相同量子態。然而，這在其忽略w:量子統計方面被證明是根本不完整的。

隨後證明，w:斯萊特行列式，即海森堡和狄拉克在 1926 年首次使用的單粒子軌道w:行列式，微不足道地滿足了精確解的反對稱性質，因此它是將w:變分原理應用於w:試探波函式的合適選擇。然後，可以將原始的哈特里方法看作是透過忽略交換來對哈特里-福克方法進行的近似。福克最初的方法過分依賴w:群論，對於當代物理學家來說過於抽象，難以理解和實施。1935 年，哈特里重新制定了該方法，使其更適合計算目的。

儘管哈特里-福克方法的物理影像更加準確，但在 20 世紀 50 年代電子計算機出現之前，由於其計算量遠大於早期的哈特里方法和經驗模型，因此很少使用。最初，哈特里方法和哈特里-福克方法都專門應用於原子，其中系統的球對稱性允許人們極大地簡化問題。這些近似方法經常（並且仍然）與w:中心場近似一起使用，以強制要求同一殼層中的電子具有相同的徑向部分，並將變分解限制為自旋本徵函式。即使如此，手工求解中等大小原子的哈特里-福克方程也是一項艱鉅的任務；小型分子需要的計算資源遠遠超過 1950 年之前所能提供的資源。

哈特里-福克演算法

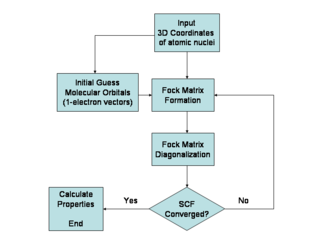
哈特里-福克方法通常用於求解w:玻恩-奧本海默近似中描述的多電子原子或分子的時間無關薛定諤方程。由於沒有已知的用於多電子系統的解（氫原子和雙原子氫陽離子是著名的單電子例外），因此該問題是透過數值方法解決的。由於哈特里-福克近似引入的非線性，這些方程使用非線性方法（例如w:迭代）來求解，這也導致了“自洽場方法”的名稱。

近似

哈特里-福克方法為了處理這一任務，做出了五個主要簡化。

• w:玻恩-奧本海默近似本身就被假設成立。完整的分子波函式實際上是每個原子核的座標以及電子的座標的函式。
• 通常，相對論效應被完全忽略。動量算符被假定為完全非相對論性的。
• 變分解被假定為有限數量基函式的w:線性組合，這些基函式通常（但並非總是）被選為w:正交的。有限基組被假定為近似完全的。
• 每個w:能量本徵函式被假定可以用單個w:斯萊特行列式來描述，即單電子波函式（即軌道）的反對稱乘積。
• 平均場近似隱含其中。由於偏離該假設而產生的影響被稱為w:電子關聯，對於自旋相反的電子來說，這些影響被完全忽略，但對於自旋平行的電子來說，這些影響被考慮在內。 （電子關聯不應與電子交換混淆，電子交換在哈特里-福克方法中得到了充分考慮）。

對最後兩個近似的放鬆導致了許多所謂的w:後哈特里-福克方法。

簡化後的演算法流程圖，展示了哈特里-福克方法

軌道的變分最佳化

變分原理指出，對於一個時間無關的哈密頓算符，任何試探波函式的能量期望值都大於或等於對應於給定哈密頓算符的真實基態波函式。因此，Hartree-Fock 能量是給定分子真實基態能量的上限。在 Hartree-Fock 方法的背景下，最佳的可能解是在 *Hartree-Fock 極限* 處；也就是說，隨著基組接近完備性，Hartree-Fock 能量的極限。（另一個是 *完全 CI 極限*，其中 Hartree-Fock 理論如上所述的最後兩個近似完全被取消。只有當這兩個極限都達到時，才能獲得精確解，直至 Born-Oppenheimer 近似。）Hartree-Fock 能量是單個 Slater 行列式的最小能量。

Hartree-Fock 方法的起點是一組近似的單電子波函式，稱為 *自旋軌道*。對於原子軌道計算，這些通常是氫原子（只有一個電子但具有適當核電荷的原子）的軌道。對於分子軌道或晶體計算，初始的近似單電子波函式通常是原子軌道線性組合 (LCAO)。

上面的軌道只以平均方式解釋了其他電子的存在。在 Hartree-Fock 方法中，其他電子的影響是在平均場理論的背景下考慮的。透過要求軌道最小化相應 Slater 行列式的能量來最佳化軌道。軌道上的結果變分條件導致了一個新的單電子算符，即 Fock 算符。在最小值處，佔據軌道是 Fock 算符的特徵解，透過它們自身之間的酉變換。Fock 算符是一個有效的單電子哈密頓算符，是兩個項的總和。第一個是每個電子的動能算符之和、核間排斥能以及核-電子庫侖吸引項之和。第二個是電子之間的庫侖排斥項，在平均場理論描述中；系統中每個電子的淨排斥能，它是透過將分子中的所有其他電子視為負電荷的平滑分佈來計算的。這是 Hartree-Fock 方法固有的主要簡化，等效於上面列表中的第五個簡化。

由於 Fock 算符取決於用於構建相應 Fock 矩陣的軌道，因此 Fock 算符的特徵函式反過來是新的軌道，可用於構建新的 Fock 算符。透過這種方式，Hartree-Fock 軌道以迭代方式最佳化，直到總電子能量的變化低於預定義的閾值。透過這種方式，計算出一組自洽的單電子軌道。然後，Hartree-Fock 電子波函式是由這些軌道構成的 Slater 行列式。根據量子力學的基本假設，Hartree-Fock 波函式可用於在 Hartree-Fock 方法和所採用的近似的框架內計算任何所需的化學或物理性質。

數學公式

Slater 行列式

在量子力學中，**Slater 行列式**是一個表示式，描述了滿足反對稱要求的多費米子系統的波函式，因此透過交換費米子改變符號而滿足泡利不相容原理。 它的名字來源於它的發現者，John C. Slater，他發表了 Slater 行列式作為一種透過使用矩陣來確保波函式反對稱性的方法。 Slater 行列式源於對電子集合的波函式的考慮，每個電子都有一個稱為自旋軌道的波函式，$\chi (\mathbf {x} )$，其中 $\mathbf {x}$ 表示單個電子的位置和自旋。同一自旋軌道內的兩個電子不會產生任何波函式。

決議

雙粒子情況

近似多粒子系統波函式的最簡單方法是取單個粒子適當選擇的正交波函式的乘積。對於具有空間座標 $\mathbf {x} _{1}$ 和 $\mathbf {x} _{2}$ 的雙粒子情況，我們有

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2}).$

此表示式在 Hartree–Fock 方法 中用作 Ansatz 來表示多粒子波函式，被稱為 Hartree 積。然而，它並不適用於 費米子，因為上述波函式不是反對稱的，而它必須是 費米子 符合 泡利不相容原理 的要求。反對稱波函式可以用以下數學方式描述：

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=-\Psi (\mathbf {x} _{2},\mathbf {x} _{1})$

此關係對於 Hartree 積並不成立。因此，Hartree 積不滿足泡利不相容原理。這個問題可以透過取兩個 Hartree 積的 線性組合 來克服

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})={\frac {1}{\sqrt {2}}}\{\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2})-\chi _{1}(\mathbf {x} _{2})\chi _{2}(\mathbf {x} _{1})\}$

$={\frac {1}{\sqrt {2}}}{\begin{vmatrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})\end{vmatrix}}$

其中係數是 歸一化因子。此波函式現在是反對稱的，不再區分費米子，也就是說：無法為特定粒子指定序數，給定的索引是可互換的。此外，如果兩個費米子的任何兩個波函式相同，它也變為零。這等同於滿足泡利不相容原理。

泛化

此表示式可以推廣到任意數量的費米子，方法是將其寫成 行列式。對於一個具有 *N* 個電子的系統，斯萊特行列式定義為

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{N})={\frac {1}{\sqrt {N!}}}\left|{\begin{matrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})&\cdots &\chi _{N}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})&\cdots &\chi _{N}(\mathbf {x} _{2})\\\vdots &\vdots &\ddots &\vdots \\\chi _{1}(\mathbf {x} _{N})&\chi _{2}(\mathbf {x} _{N})&\cdots &\chi _{N}(\mathbf {x} _{N})\end{matrix}}\right|\equiv \left|{\begin{matrix}\chi _{1}&\chi _{2}&\cdots &\chi _{N}\\\end{matrix}}\right|,$

其中在最終表示式中，引入了緊湊的符號：費米子座標的歸一化常數和標籤是理解的 - 只有波函式被展示。對於雙粒子情況，哈特里積的線性組合可以清楚地看出與N = 2 的斯萊特行列式相同。可以看出，使用斯萊特行列式確保了從一開始就得到一個反對稱函式；對稱函式被自動拒絕。同樣，使用斯萊特行列式確保了符合 泡利不相容原理。事實上，如果集合 {χ_i } 是 線性相關的，則斯萊特行列式消失。特別地，當兩個（或更多）自旋軌道相同時，情況就是這樣。在化學中，人們用這樣的說法來表達這一事實：沒有兩個電子可以佔據同一個自旋軌道。一般情況下，斯萊特行列式是透過 拉普拉斯展開來計算的。在數學上，斯萊特行列式是一個反對稱張量，也被稱為 外積。

在 哈特里-福克理論中，單個斯萊特行列式被用作電子波函式的近似值。在更精確的理論中（例如 組態相互作用 和 多組態自洽場），需要斯萊特行列式的線性組合。

S. F. Boys 提出了“detor”這個詞來描述一般型別的斯萊特行列式， 但這個詞很少使用。

與受泡利不相容原理約束的 費米子 不同，兩個或多個 玻色子 可以佔據相同的單粒子量子態。描述相同 玻色子 系統的波函式在粒子交換下是對稱的，可以用 永久行列式 來展開。

福克算符

主條目：w:福克矩陣

因為 w:電子分子哈密頓量 的電子-電子排斥項涉及兩個不同電子的座標，所以有必要以近似的方式重新表達它。在這種近似下（在 哈特里-福克演算法 中概述），除核-核排斥項之外的所有精確哈密頓量的項都被重新表達為下面概述的單電子運算元的總和，用於閉殼層原子或分子（每個空間軌道中有兩個電子）。 每個算符符號後面的“(1)”只是表示算符本質上是1電子的。

${\hat {F}}[\{\phi _{j}\}](1)={\hat {H}}^{\text{core}}(1)+\sum _{j=1}^{N/2}[2{\hat {J}}_{j}(1)-{\hat {K}}_{j}(1)]$

其中

${\hat {F}}[\{\phi _{j}\}](1)$

是由軌道 $\phi _{j}$ 生成的單電子福克算符，並且

${\hat {H}}^{\text{core}}(1)=-{\frac {1}{2}}\nabla _{1}^{2}-\sum _{\alpha }{\frac {Z_{\alpha }}{r_{1\alpha }}}$

是單電子核心 哈密頓算符。 同時

${\hat {J}}_{j}(1)$

是 庫侖算符，定義了第 j 個軌道中兩個電子之間相互排斥的能量。 最後

${\hat {K}}_{j}(1)$

是 交換算符，定義了由於總 n 電子波函式的反稱性而產生的電子交換能量。 這個（所謂的）“交換能量”算符 K 只是斯萊特行列式的一個產物。 尋找哈特里-福克單電子波函式現在等效於求解本徵函式方程

${\hat {F}}(1)\phi _{i}(1)=\epsilon _{i}\phi _{i}(1)$

其中 $\phi _{i}\;(1)$ 是一組單電子波函式，稱為哈特里-福克分子軌道。

原子軌道線性組合

主要文章: w:基組 (化學) 和 w:基組

通常，在現代的哈特里-福克計算中，單電子波函式用 原子軌道的線性組合 近似。 這些原子軌道被稱為 斯萊特型軌道。 此外，為了節省大量的計算時間，使用的“原子軌道”實際上是由一個或多個 高斯型軌道 的線性組合組成的，而不是斯萊特型軌道。

在實踐中，使用了各種基組，其中大多數由高斯函式組成。在某些應用中，為了產生一組正交基函式，會執行正交化方法，例如w:Gram-Schmidt過程。原則上，當計算機透過將w:重疊矩陣有效地轉換為w:單位矩陣來求解Roothaan-Hall方程時，這可以節省計算時間。然而，在大多數用於分子Hartree-Fock計算的現代計算機程式中，由於正交化的數值成本高，以及用於求解w:廣義特徵值問題（Roothaan-Hall方程就是一個例子）的更有效、通常是稀疏的演算法的出現，因此沒有遵循此過程。

數值穩定性

w:數值穩定性在這個過程中可能是一個問題，並且有各種方法可以克服這種不穩定性。最基本且普遍適用的方法之一稱為F混合或阻尼。使用F混合，一旦計算出一個單電子波函式，它就不會直接使用。相反，使用該計算波函式與之前該電子的波函式的某種組合，最常見的是計算波函式和緊接其前的波函式的簡單線性組合。Hartree在原子計算中採用的一個巧妙的策略是增加核電荷，從而將所有電子拉得更近。隨著系統的穩定，逐漸將其減少到正確的電荷。在分子計算中，有時透過首先計算正離子的波函式，然後使用這些軌道作為中性分子的起點，來使用類似的方法。現代分子Hartree-Fock計算機程式使用多種方法來確保Roothaan-Hall方程的收斂。

弱點、擴充套件和替代方案

在“Hartree-Fock演算法”部分概述的五個簡化中，第五個通常是最重要的。忽略電子相關性會導致與實驗結果出現較大偏差。為了將電子相關性包含到多電子波函式中，人們設計了許多方法來克服這種弱點，這些方法統稱為w:後Hartree-Fock方法。其中一種方法，w:Møller-Plesset微擾理論，將相關性視為Fock算符的微擾。其他方法將真正的多電子波函式展開為Slater行列式的線性組合，例如w:多組態自洽場、w:組態相互作用、w:二次組態相互作用和完全活性空間自洽場 (CASSCF)。還有一些其他方法（例如變分量子蒙特卡羅）透過將Hartree-Fock波函式乘以相關函式（“Jastrow”因子）來修改Hartree-Fock波函式，該項明確地是多個電子的函式，不能分解成獨立的單粒子函式。

在某些情況下，Hartree-Fock計算的一種替代方法是w:密度泛函理論，它處理交換和相關能量，儘管是近似地。實際上，通常使用兩種方法的混合計算，流行的B3LYP方案就是一種這樣的w:混合泛函方法。另一個選擇是使用w:現代價鍵方法。

軟體包

有關已知處理Hartree-Fock計算（特別是針對分子和固體）的軟體包列表，請參見w:量子化學和固態物理軟體列表.

來源

• Levine, Ira N. (1991). Quantum Chemistry (第 4 版). 新澤西州英格伍德懸崖: 普倫蒂斯·霍爾. pp. 455–544. ISBN 0-205-12770-3.
• Cramer, Christopher J. (2002). Essentials of Computational Chemistry. 奇切斯特: 約翰·威利父子公司. pp. 153–189. ISBN 0-471-48552-7.
• Szabo, A.; Ostlund, N. S. (1996). Modern Quantum Chemistry. 紐約米尼奧拉: 多佛出版公司. ISBN 0-486-69186-1.

Slater 行列式

雙粒子情況

近似多粒子系統波函式的最簡單方法是取適當選擇的正交個體粒子波函式的乘積。對於具有空間座標$\mathbf {x} _{1}$和$\mathbf {x} _{2}$的兩個粒子情況，我們有

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2}).$

該表示式在w:Hartree-Fock方法中用作多粒子波函式的w:假設，被稱為w:Hartree乘積。然而，它對於w:費米子並不令人滿意，因為上述波函式不是反對稱的，而它必須是w:費米子根據w:泡利不相容原理的要求。反對稱波函式可以用數學方式描述如下

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})=-\Psi (\mathbf {x} _{2},\mathbf {x} _{1})$

這對於Hartree乘積不成立。因此，Hartree乘積不滿足泡利原理。這個問題可以透過對兩個Hartree乘積進行w:線性組合來克服

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2})={\frac {1}{\sqrt {2}}}\{\chi _{1}(\mathbf {x} _{1})\chi _{2}(\mathbf {x} _{2})-\chi _{1}(\mathbf {x} _{2})\chi _{2}(\mathbf {x} _{1})\}$

$={\frac {1}{\sqrt {2}}}{\begin{vmatrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})\end{vmatrix}}$

其中係數是w:歸一化因子。此波函式現在是反對稱的，不再區分費米子，也就是說：無法為特定粒子指定序數，給定的索引是可以互換的。此外，如果兩個費米子的任何兩個波函式相同，它也將變為零。這相當於滿足泡利不相容原理。

泛化

該表示式可以推廣到任意數量的費米子，方法是將其寫成w:行列式。對於一個N電子系統，Slater行列式定義為

$\Psi (\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{N})={\frac {1}{\sqrt {N!}}}\left|{\begin{matrix}\chi _{1}(\mathbf {x} _{1})&\chi _{2}(\mathbf {x} _{1})&\cdots &\chi _{N}(\mathbf {x} _{1})\\\chi _{1}(\mathbf {x} _{2})&\chi _{2}(\mathbf {x} _{2})&\cdots &\chi _{N}(\mathbf {x} _{2})\\\vdots &\vdots &\ddots &\vdots \\\chi _{1}(\mathbf {x} _{N})&\chi _{2}(\mathbf {x} _{N})&\cdots &\chi _{N}(\mathbf {x} _{N})\end{matrix}}\right|\equiv \left|{\begin{matrix}\chi _{1}&\chi _{2}&\cdots &\chi _{N}\\\end{matrix}}\right|,$

在最後的表示式中，引入了一種緊湊的記號：歸一化常數和費米子座標的標籤被理解 - 只有波函式被展示出來。對於雙粒子情況，哈特里乘積的線性組合可以清楚地看作與N = 2 的斯萊特行列式相同。可以看出，使用斯萊特行列式確保從一開始就得到一個反對稱函式；對稱函式被自動拒絕。同理，使用斯萊特行列式確保符合w:泡利不相容原理。事實上，如果集合{χ_i} 是w:線性相關的，則斯萊特行列式為零。特別地，當兩個（或更多）自旋軌道相同時，情況就是這樣。在化學中，人們用這句話來表達這個事實，即不能有兩個電子佔據相同的自旋軌道。通常，斯萊特行列式透過w:拉普拉斯展開進行計算。在數學上，斯萊特行列式是一個反對稱張量，也稱為w:外積。

在w:哈特里-福克理論中，單個斯萊特行列式被用作電子波函式的近似。在更精確的理論（如w:組態相互作用和w:多組態自洽場）中，需要斯萊特行列式的線性組合。

S. F. Boys 提出用“detor”來描述一般型別的斯萊特行列式，但這個術語很少使用。

與受到泡利不相容原理約束的w:費米子不同，兩個或多個w:玻色子可以佔據系統相同的量子態。描述相同w:玻色子系統的波函式在粒子交換下是對稱的，並且可以用w:永年式來展開。

Fock矩陣

在w:哈特里-福克方法中，Fock矩陣是近似於給定量子系統在一組給定的基向量中單電子w:能量算符的矩陣。

它最常在嘗試解決原子或分子系統的w:Roothaan方程時在w:計算化學中形成。Fock矩陣實際上是量子系統真實哈密頓量算符的近似。它包括電子-電子排斥的影響，但只是以平均的方式。重要的是，由於Fock算符是一個單電子算符，它不包括w:電子相關能量。

Fock矩陣由Fock算符定義。對於假設w:閉殼軌道和單行列式波函式的限制情況，第i個電子的Fock算符由下式給出：

${\hat {F}}(i)={\hat {h}}(i)+\sum _{j=1}^{n/2}[2{\hat {J}}_{j}(i)-{\hat {K}}_{j}(i)]$

其中

${\hat {F}}(i)$ 是系統中第i個電子的Fock算符，

${\hat {h}}(i)$ 是第i個電子的w:單電子哈密頓量，

$n$ 是電子的數量，${\frac {n}{2}}$ 是閉殼系統中佔據軌道的數量，

${\hat {J}}_{j}(i)$ 是w:庫侖算符，定義了系統中第j個和第i個電子之間的排斥力，

${\hat {K}}_{j}(i)$ 是w:交換算符，定義了交換兩個電子時產生的量子效應。

庫侖算符乘以2，因為每個佔據軌道上有兩個電子。交換算符不乘以2，因為它只有在電子自旋與第i個電子相同的情況下才會有非零結果。

對於具有不成對電子的體系，福克矩陣有很多選擇。

Hartree-Fock (HF) 或自洽場 (SCF)

密度泛函理論

與量子態對稱性的關係

具有單值多粒子波函式的泡利不相容原理等同於要求波函式反對稱。反對稱的雙粒子態表示為態的疊加，其中一個粒子處於$\scriptstyle |x\rangle$態，另一個粒子處於$\scriptstyle |y\rangle$態。

$|\psi \rangle =\sum _{x,y}A(x,y)|x,y\rangle$

交換後的反對稱性意味著A(x,y) = −A(y,x)。這意味著A(x,x) = 0，這就是泡利不相容原理。這在任何基底中都是成立的，因為么正基底變換會保持反對稱矩陣的反對稱性，雖然嚴格來說，A(x,y) 不是矩陣，而是反對稱的二階w:張量。

反之，如果對角量A(x,x)在每個基底中都為零，那麼波函式分量

$A(x,y)=\langle \psi |x,y\rangle =\langle \psi |(|x\rangle \otimes |y\rangle )$

必然是反對稱的。為了證明這一點，考慮矩陣元

$\langle \psi |((|x\rangle +|y\rangle )\otimes (|x\rangle +|y\rangle ))\,$

這是零，因為兩個粒子同時處於疊加態$\scriptstyle |x\rangle +|y\rangle$的機率為零。但它等於

$\langle \psi |x,x\rangle +\langle \psi |x,y\rangle +\langle \psi |y,x\rangle +\langle \psi |y,y\rangle \,$

右側的第一項和最後一項是對角元素，為零，整個和為零。所以波函式矩陣元服從

$\langle \psi |x,y\rangle +\langle \psi |y,x\rangle =0\,$.

或

$A(x,y)=-A(y,x)\,$

泡利原理在高階量子理論中的應用

根據w:自旋統計定理，自旋為整數的粒子佔據對稱量子態，而自旋為半整數的粒子佔據反對稱態。此外，根據量子力學原理，自旋值只能為整數或半整數。在相對論w:量子場論中，泡利原理來自於對半整數自旋粒子施加虛時間旋轉算符。由於在非相對論情況下，粒子可以具有任何統計特性和任何自旋，因此無法在非相對論量子力學中證明自旋統計定理。

在一維空間中，玻色子和費米子都可以遵守不相容原理。具有無限強度的德爾塔函式排斥相互作用的一維玻色氣體等效於自由費米子氣體。造成這種情況的原因是，在一維空間中，粒子的交換要求它們彼此穿過；對於無限強的排斥力，這種情況不可能發生。這種模型由量子w:非線性薛定諤方程描述。在動量空間中，不相容原理也適用於具有德爾塔函式相互作用的玻色氣體中的有限排斥力， 以及對於相互作用自旋和w:哈伯德模型在一維空間中，以及對於其他可以透過w:貝特假設求解的模型。透過貝特假設求解的模型中的基態是一個費米球。

密度泛函理論

參考文獻

另請參閱有關如何新增參考文獻的編輯本書說明w:奈米技術/關於#如何貢獻。

---

Hartree–Fock 方法