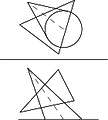
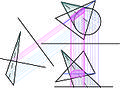
描述幾何/複雜立體交叉

圓柱體

直線與立體的交叉使用截面檢視找到穿刺點。

1. 將給定檢視中給定的直線視為給定立體截面的邊緣檢視。 2. 直線在該檢視中與圓柱底面交叉的點即為穿刺點。 3. 將這些點向下投影到另一檢視中，直到它們與給定的直線交叉，即可找到穿刺點。

直線與圓柱體的交叉

使用垂直截面平面。

1. 在俯檢視中，將給定直線視為垂直截面平面的邊緣檢視。 2. 找到直線與底面交叉的點。將這些穿刺點向下投影到正檢視。 3. 穿刺點即為這些點在正檢視中與直線相交的位置。

直線與傾斜圓柱體的交叉

建立與圓柱軸平行的截面平面。

1. 在正檢視中，在給定直線上選擇兩個點，並繪製兩條平行於軸且經過這兩個點的直線。 2. 標記這兩條直線與圓柱底面邊緣檢視相交的點。將這些點投影到俯檢視，直到它們與底面相交。 3. 繪製平行於軸線、指向圓柱另一個底面的直線。 4. 這兩條直線與給定直線相交的位置即為兩個穿刺點。

平面與圓柱體的交叉

圓柱體由無數條平行於軸線且沿著底面的直線組成。在一個檢視中建立一個方便的截面平面，該平面包含一個穿刺點，並將其投影以找到跡線並定位另一個檢視中的穿刺點。

1. 在俯檢視中，找到給定平面兩側與圓柱底面交叉的視在穿刺點。 2. 將這些穿刺點投影到正檢視，並在它們與平面的同側相遇的地方標記它們。 3. 為了找到構成交叉平面的更多點，可以使用截面平面和跡線：a. 在俯檢視中選擇底面上的一個點（應位於給定平面內，並沿著圓柱的底面）。 b. 繪製一條包含該點的直線（代表截面平面的邊緣檢視），穿過給定平面。 c. 將這條直線和穿刺點向下投影到正檢視。穿刺點（在正檢視中）位於這條直線上。 d. 將這些穿刺點（在正檢視中）連線起來，並考慮可見性，以找到交叉平面。

例如，問題，請參閱檔案“問題 1 直線與圓柱體的交叉”和“問題 2 平面與圓柱體的交叉”。

問題 1 直線與圓柱體的交叉
問題 1 解答

問題 2 平面與圓柱體的交叉
問題 2 解答

圓錐體

平面與圓錐體的交叉（給出兩個檢視）

在一個檢視中繪製一條平行於折線且穿過交叉平面上一個點的直線。將這條直線及其上的點轉移到另一個給定檢視，以獲得真實長度的直線。繪製垂直於真實長度直線的折線，並將圓錐上的點轉移到輔助檢視。將交叉平面轉移到輔助檢視以顯示平面的邊緣檢視，並將其視為截面平面。從底平面邊緣檢視繪製到圓錐頂點的直線。將這些直線轉移到其他兩個檢視。在輔助檢視中找到截面平面與圓錐線之間的交叉點，並將這些點轉移回其他兩個檢視以找到交叉點。確定可見性。

問題 1
問題 1 - 在交叉線上選擇任意點
問題 1 - 從頂點延伸直線
問題 1 - 找到穿刺點

直線與圓錐體的交叉（給出兩個檢視）

在正檢視中選擇直線上的兩個任意點。從頂點繪製穿過這兩個點的直線以與圓錐底平面的邊緣檢視相交，標記這些交叉點。將直線上的兩個任意點垂直投影到俯檢視上的交叉線上，並在俯檢視中從頂點繪製經過這兩個點的直線。將兩個標記的交叉點投影到俯檢視，並標記它與之前從頂點繪製的穿過兩個投影任意點的直線的交點。連線這兩個點以建立底平面的截面平面。將這條直線在俯檢視中與圓錐底面相交的點連線到頂點，這兩條直線與交叉線相交的位置即為直線的穿刺點。將穿刺點帶回正檢視。

問題 2
問題 2 - 找到一條真實長度的直線
問題 2 - 從真實長度直線建立交叉平面的邊緣檢視
問題 2 - 從圓錐頂點延伸直線
問題 2 - 找到交叉點

檔案：DescGeoSphere.pptx

檔案：Fig1.1

球體

球體的截面

給出球體及其截面的兩個檢視。（圖 1.1）

要找到球體的真實截面，我們繪製一個輔助檢視。

該檢視的折線必須平行於直線（另一個檢視中顯示的截面邊緣檢視）。（圖 1.2）

這將使我們獲得球體截面的真實尺寸。輔助檢視是透過簡單地轉移距離來構建的。（圖 1.3）

直線與球體的交叉：（圖 2.1）

我們可以使用上述結構來找出直線與球體的穿刺點。為此，我們假設兩個檢視中的一個檢視中的直線是截面平面的邊緣檢視。（圖 2.2）

利用這些資訊，我們可以在另一個檢視中構建球體的相應截面。直線與該截面相交的點可以轉移回直線上，以找到直線與球體的穿刺點。我們可以將這些點投影回第一個檢視。（圖 2.3）

練習題：（含解答）（參考圖片名稱：問題 1. 找到 (a) 球體的真實截面和 (b) 穿刺點解答 1(a) 解答 1(b) 問題 2 解答 2 (a&b)

複雜立體之間的交叉

複雜立體與複雜立體的交叉圓柱體與圓柱體圓錐體與圓柱體首先確定這兩個複雜立體是否具有相互平行的軸線。如果不是，第一步是構建一個包含一條平行於這兩個複雜立體軸線的直線的平面，該直線在俯檢視中與每個立體相交。如果形狀的表面不共面，則在正檢視中將一個形狀延伸，直到它們具有一個公共底面平面。構建與之前構建的平面平行的、與兩個立體底面相交的截面平面，以確定平面與立體之間的交叉點，如圖所示。將第二步中獲得的交叉點投影到另一個檢視中相應的立體上。利用這些交叉點，構建平行於該立體軸線的直線，使其在您用於上述步驟的相同檢視中與立體相交。標記來自同一截面平面的交叉點。兩個複雜立體在這些點相交。連線交叉點以獲得兩個立體相互交叉的形狀。將上面獲得的對應於立體的點投影到另一個檢視中，以獲得交叉平面的形狀。注意：您應該使用大量交叉平面，並遵循上述步驟以獲得準確的交叉形狀。

為了更好地理解這個主題，請做下面指定的練習題。

描述幾何
描述幾何
描述幾何
描述幾何
複雜立體交叉問題 1 的圖片
複雜立體交叉問題 1 的解答
複雜立體交叉問題 2 的圖片
複雜立體交叉問題 2 的解答

複雜立體與平面立體的交叉

將平面立體分解成單個表面，並分別處理每個表面。對於平面立體上的每個表面，找到表面與複雜立體之間的交叉點。（俯檢視）利用穿刺點將這些交叉點投影到正檢視。這些將是兩個立體相交的點。（俯檢視/正檢視）如果需要更多點來完成交叉形狀，請在每個表面上建立直線，並使用之前相同的方法找到更多交叉點。重複使用平面立體上的其他表面，直到找到完整的交叉形狀。

示例問題 1
示例問題 1 解答
示例問題 2
示例問題 2 解答
設定
解答
設定
解答