描述幾何/圓錐軌跡

定義

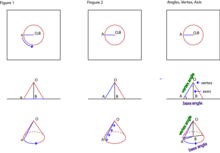
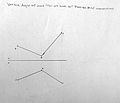
軌跡（locus/loci）是滿足給定條件的一組解。[[[[Media:|thumbnail]]]] 根據具體情況，軌跡可以是不同的解。在圖A中，有一條垂直軸BO和一個點a。當點a繞BO旋轉時，點a形成的路徑是一個圓。在這個給定的條件下，軌跡是點a繞BO旋轉時形成的圓形路徑，因為這個圓是所有與BO的距離與點a相同的點的集合。在圖B中，有一條垂直軸BO，線段AO與BO相交形成∠AOB。當AO繞BO旋轉時，AO形成的路徑是一個錐形的表面。因此，在這個特定的條件下，軌跡AO是一個錐面，因為這個表面是三維空間中所有可以用AO表示的線段的集合。

兩個相交物體的軌跡將是滿足交點的所有解。如果圓錐“A”和圓錐“B”共享一個頂點並具有相同的母線長，則有三種可能的解：1個交點、2個交點或沒有交點。如果兩條軸之間的角度小於兩個頂角之和，則有兩個軌跡交點解。如果兩條軸之間的角度等於兩個頂角之和，則只有一個解。如果兩條軸之間的角度大於兩個頂角之和，則沒有解。

求解圓錐軌跡交線

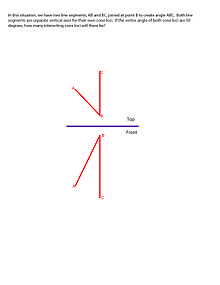
考慮兩條相交線AO和BO的頂檢視和正檢視，夾角為∠AOB。由線繞AO和BO旋轉（形成圓錐）形成的頂角分別為α和β。構造檢視，使一個檢視顯示兩個圓錐軸的真實長度（正檢視），另一個檢視顯示兩個圓錐軸的點檢視（頂檢視）。在真實長度檢視中，構造一個任意半徑的圓，使其與圓錐的母線相交。連線圓錐和圓的交點，形成圓錐的底面。標記每個圓錐底面與另一個圓錐底面相交的所有點。這些是圓錐交點的軌跡。從軌跡到頂點的線是每個圓錐與其相鄰圓錐交匯的邊緣。

如果圓錐的軸不是線段，而是無限長的直線，則需要測試是否存在兩個以上的解。產生圓錐面的旋轉線可以從頂點指向不同的方向，從而產生兩個圓錐的可能性。因此，對於四個圓錐，最多可以有四個軌跡交點。