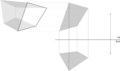
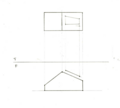
描述幾何/距離
點和直線之間的真實距離是它們之間的最短距離。首先,沿平行於直線的摺疊線投影輔助檢視以找到其真實長度。確保也投影點。其次,沿垂直於直線的摺疊線建立另一個輔助檢視以找到它點檢視。兩點之間的距離是真實距離。
平行線:透過沿平行摺疊線投影它們來找到平行線的真實長度(找到其中一條線的真實長度將找到另一條線的真實長度)。接下來,透過製作垂直摺疊線並再次投影直線來找到兩條線的點檢視。兩點之間的距離是兩條平行線之間的真實距離。
異面直線:找到兩條直線中的任何一條的真實長度,但仍然投影兩條直線穿過摺疊線。然後找到真實長度的直線的點檢視。繪製一條垂直於直線的線,該線穿過該點,這是異面直線之間的距離。
為了找到直線和平面之間的距離,第一步是將直線放在點檢視中。這可以透過建立一個垂直於真實長度的直線的摺疊線並使用轉移距離來構建檢視來完成。
如果直線和平面平行,這種結構也會將平面放在邊緣檢視中。直線和平面之間的距離將是從點檢視中的直線到邊緣檢視中的平面的直線的長度。邊緣檢視中的平面將顯示為一條線,但它可以在任何方向無限延伸。
-
問題
-
解決方案
如果直線和平面不平行(即當直線處於點檢視時,平面不處於邊緣檢視),那麼直線將與平面在某一點相交,距離為零。您可以透過找到平面在邊緣檢視中的位置並看到直線最終將刺穿平面來驗證這一點。
-
問題
-
解決方案
找到與水平線成一定角度的距離涉及到找到兩個點之間的距離,這兩個點不共享垂直於視點方向的平面。為了找到這個距離,首先要將這兩個給定點用一條線段連線起來。然後,首先在點檢視中構建該線,以便可以將其構建為真實長度,從而給出兩點之間的真實距離。
-
圖示說明如何在空間中構建兩點之間的距離。
示例問題
氣象站 A 位於海拔 3250 米的山上。氣象站 B 位於距離氣象站 A 10 公里的海拔 4500 米的山峰上。氣象局有興趣將這兩個站與海拔 7000 米的氣象氣球結合起來用作三角測量裝置。氣象氣球必須放置在使它完成等邊三角形的位置。氣象局可以在哪裡放置氣球,氣球與每個氣象站之間的距離是多少?
-
示例問題的解決方案
在這種情況下,找到點到立體的最短距離意味著找到給定點和最靠近該立體的最近面的最近點之間的最短距離,假設該立體具有平面面。因此,在做這個問題時,將一個正在互動的元素隔離起來是有用的,在這種情況下,是最接近的面和正在考慮的點。這簡化了找到點和平面之間的最短距離的問題。
為了找到點和平面之間的最短距離,首先必須找到平面在邊緣檢視中的檢視。透過將平面顯示在邊緣檢視中,人們進一步簡化了問題,使其變為找到點和直線之間的最短距離。一旦你有了平面在邊緣檢視中的位置,你必須建立一個垂直於平面的直線。在將這條直線轉移回先前的檢視後,可以使用穿刺點結構來找到平面中最靠近給定點的點,因此是立體中最靠近給定點的點。
-
演示如何拆解立體,以便可以找到最靠近外部點的邊的點。
示例問題
超級羊駝正在逃避一立方千米邪惡的飛行惡魔寶寶,這些寶寶是來自短蛋糕博士。每個飛行的惡魔寶寶佔據一立方米的空間。立方體的底部距離地面 2 公里,並且傾斜的方式使得四個邊指向一個基點。如果短蛋糕博士在超級羊駝上空 10 公里,並且在超級羊駝的頂檢視中距離立方體中心 8 公里,立方體中心位於超級羊駝的 N60 度 E 方向,那麼哪個飛行惡魔寶寶會首先到達超級羊駝?
-
示例問題的解決方案
為了求解直線到立體的最短距離,這個問題必須被視為求解直線到平面的最短距離。立體中最靠近該直線的面的應該被視為這個獨立的平面。然後,該過程變得相當簡單:您所要做的就是執行找到直線到平面的最短距離的構造(如上所述,它本身只是簡化為找到點和直線之間的最短距離的構造)。
重申一下,找到直線到平面的最短距離的構造如下:首先必須構建一個檢視,在該檢視中,直線以點檢視顯示。如果直線和平面平行,則平面應該在直線以點檢視顯示的同一檢視中以邊緣檢視顯示(否則,直線和平面最終將相交,因此它們之間的最短距離為零,如上所述)。然後所要做的就是用一條垂直線將點檢視中的直線連線到平面的邊緣檢視。這條垂直線是真實長度,是直線和平面之間的最短距離,在這種情況下,這也意味著它是直線和立體之間的最短距離。如果需要,您可以透過使用轉移距離將最短距離線投影到其他檢視中。
如果實體是一個圓形面的實體,例如圓柱體,要找到直線和實體之間的最短距離,可以將實體抽象為一條直線——其中心線——並使用查詢直線和點之間最短距離的構造方法。你只需要將實體的厚度,即實體的直徑加回到最終檢視中,就可以得到實體和直線之間的實際比例距離。
示例問題
[edit | edit source]一座著名的義大利鐘樓面臨倒塌的危險。在圖紙中,它被近似地表示為一個斜圓柱。為了支撐鐘樓,工程師們在鐘樓旁邊的地面上放置了一個傾斜的支架,現在他們想用鋼索連線鐘樓和支架。為了開始,工程師們想知道連線鐘樓和支架的鋼索的最短長度是多少;換句話說,他們想知道鐘樓和支架之間的最短距離是多少。找到這個距離。使用 1 毫米等於 5 英尺的比例;鐘樓的半徑是 10 英尺(2 毫米)。
-
示例問題
解決方案:為了解決這個問題,你只需要將圓柱體的中心線視為一條直線,然後使用上面描述的查詢點和直線之間最短距離的構造方法。
-
示例問題的解決方案
從平面到實體的距離
[edit | edit source]平面和實體之間的最短距離可以透過將實體離平面最近的面視為一個獨立的平面來找到。這樣,問題就簡化為找到兩個平面之間的最短距離,這就是你必須進行的構造,以找到原始平面和實體之間的最短距離。再次強調,為了進行這種構造,兩個平面必須平行,否則它們最終會相交,使它們之間的最短距離為零。
查詢兩個平面之間最短距離的構造最終簡化為查詢直線和平面之間的最短距離。你必須首先建立一個檢視,在這個檢視中,兩個平面都以邊緣檢視顯示,由於平面是平行的,這意味著只需要建立一個平面上的邊緣檢視。然後,你可以在其中一條邊緣檢視線路上選擇一個任意點,從該點可以畫一條垂直線到另一條邊緣檢視線上。這條直線處於真實長度,是兩個平面之間的最短距離。為了將最短距離線投射到其他檢視,你必須執行穿刺點構造,以找到最短距離線與平面相交的點。
示例問題
[edit | edit source]一位建築師在他的建築物的一側屋頂上方放置了一個遮陽裝置。遮陽裝置平行於屋頂表面。連線遮陽裝置和屋頂的支撐線的最短長度是多少(從遮陽裝置平面到實體屋頂表面的最短距離)?
-
如何找到平行於彼此的平面和實體表面的最短距離的示例問題
解決方案:這個問題有點像一個陷阱問題。它測試你對推動問題概念的理解程度。在這種情況下,平面與實體的最近面均勻平行。實體的正面已經顯示在正面檢視中的真實形狀,因為它與正面檢視和頂檢視中的摺疊線平行。這意味著平面在正面檢視中的邊緣檢視以真實長度顯示,因為它與實體正面中的一個側面平行。由於所有這一切都是正確的,這意味著從平面到實體最近表面的最短距離在從平面到表面的所有垂線上都是一樣的。因此,從平面到表面的最短距離已經隱含地顯示在該正面檢視中;如果你願意,你只需要測量那個距離。
-
示例問題的解決方案
從實體到實體的距離
[edit | edit source]當求解兩個實體之間的最短距離時,將兩者都視為直線,使用直線到直線的方法。例如,取兩個圓柱體或一個錐體,求解它們軸之間的最短距離。然後考慮實體的深度;從中心到實體表面的距離。