描述幾何/透過旋轉求距離

為了求得點與直線或點與平面的距離，需要將直線旋轉到真長位置。對於點和直線：將直線垂直於折線旋轉，從而找到直線的點檢視。對於點和平面：需要將直線垂直於折線旋轉，從而找到直線的稜邊檢視。然後可以測量點之間的距離或點與直線的距離。

求點與直線之間的最短距離

1. 在一個檢視中（任意選擇一個檢視）旋轉直線，使其平行於折線。
2. 將新的點轉移到其下方另一個檢視中。現在這條直線處於真長位置。
3. 將真長位置的直線旋轉，使其垂直於折線。
4. 將新的點轉移到對面的檢視中，以獲得直線的點檢視。

現在可以測量這兩個點之間的距離。

以下是一個示例問題（解決方案方法位於問題下方）。

示例一：求點與直線之間的最短距離 紅色線條表示影像中的下一步操作。

1. 步驟A/B）在一個檢視中旋轉直線（任意選擇一個檢視，在此示例中，使用頂檢視），使其平行於折線。
2. 步驟C）將新的點轉移到其下方另一個檢視中。現在這條直線處於真長位置。
3. 步驟D）將真長位置的直線旋轉，使其垂直於折線。
4. 步驟E）將新的點轉移到對面的檢視中，以獲得直線的點檢視。
5. 現在可以測量這兩個點之間的距離。

以下是解決方案

求點與平面之間的最短距離

1. 選擇平面的其中一面旋轉到真長位置。在接下來的步驟中，將使用這條線進行旋轉。在此示例中，使用平面的底邊。
2. 在一個檢視中（任意選擇一個檢視，在此示例中，使用頂檢視）旋轉這條線，使其平行於折線。同時將最後一個點旋轉過來。（有關更多說明，請參見旋轉平面）。
3. 將兩個新的點轉移到其下方另一個檢視中。現在這條直線處於真長位置。
4. 將真長位置的直線旋轉，使其垂直於折線，從而找到平面的稜邊檢視。
5. 將新的點轉移到對面的檢視中，以獲得直線的點檢視。

現在可以測量這兩個點之間的距離。請注意，在測量從點到稜邊檢視中平面的距離時，測量線必須垂直於稜邊檢視中的平面。否則無法找到最短距離。

以下是一個示例問題（解決方案方法位於問題下方）。

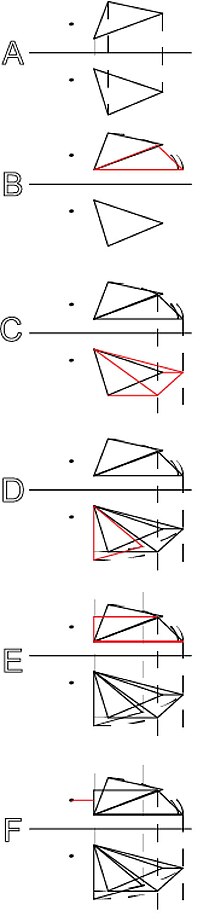
示例二：求點與平面之間的最短距離 紅色線條表示影像中的下一步操作。

1. 步驟A）選擇平面的其中一面旋轉到真長位置。在接下來的步驟中，將使用這條線進行旋轉。在此示例中，使用平面的底邊。
2. 步驟B）在一個檢視中（任意選擇一個檢視，在此示例中，使用頂檢視）旋轉這條線，使其平行於折線。同時將最後一個點旋轉過來。（有關更多說明，請參見旋轉平面）。
3. 步驟C）將兩個新的點轉移到其下方另一個檢視中。現在這條直線處於真長位置。
4. 步驟D）將真長位置的直線旋轉，使其垂直於折線，從而找到平面的稜邊檢視。
5. 步驟E）將新的點轉移到對面的檢視中，以獲得直線的點檢視。
6. 步驟F）現在可以測量這兩個點之間的距離。請注意，在測量從點到稜邊檢視中平面的距離時，測量線必須垂直於稜邊檢視中的平面。否則無法找到最短距離。

以下是解決方案