數位電路/加法器

半加器

考慮將兩個二進位制數加在一起

我們看到，“二進位制”列中的位是在進位時生成的。半加器是一個電路，它將兩個位加在一起並輸出這兩個位的總和。半加器有兩個輸出：和和進位。和表示 A+B/2 的整數除法的餘數，而進位是結果。這可以表示如下

• ${\mbox{S}}=A\oplus B$
• ${\mbox{C}}=AB\,$

A B A+B S C 0 0 0 0 0 0 1 1 1 0 1 0 1 1 0 1 1 2 0 1

全加器

半加器有一個主要的侷限性，即它們不能接受來自前一級的進位位，這意味著它們不能連線在一起以新增多位數。但是，半加器的兩個輸出位也可以表示結果 A+B=3，因為和和進位都為高電平。

因此，全加器可以接受三個位作為輸入。通常，一位被稱為進位輸入位。全加器可以級聯在一起，透過將一個輸出的進位連線到下一個輸入的進位，來產生任意位數的加法器。

A B Cin A+B+Cin S Cout 0 0 0 0 0 0 0 0 1 1 1 0 0 1 0 1 1 0 0 1 1 2 0 1 1 0 0 1 1 0 1 0 1 2 0 1 1 1 0 2 0 1 1 1 1 3 1 1

全加器通常顯示為一個單元。和輸出通常在塊的底部，進位輸出在左側，因此這些裝置可以連線在一起，最高有效位在最左邊

行波進位加法器

行波進位加法器只是幾個串聯連線的全加器，因此進位必須透過每個全加器才能完成加法。行波進位加法器在所有加法器中需要的硬體最少，但它們是最慢的。

下圖顯示了一個四位加法器，它將數字 A[3:0] 和 B[3:0] 以及一個進位輸入加在一起，生成 S[3:0] 和進位輸出。

全加器中的傳播延遲

真正的邏輯閘不會對輸入做出瞬時反應，因此數位電路具有最大速度。通常，數位電路的延遲以門延遲來衡量，因為這使得可以為不同的器件計算設計的延遲。與門和或門具有名義上的 1 門延遲，異或門具有 2 門延遲，因為它們實際上是由與門和或門的組合組成的。

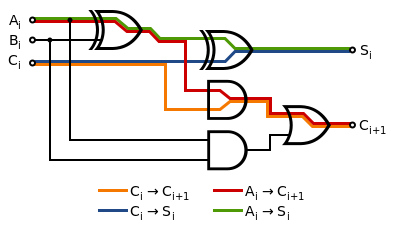
全加器塊具有以下最壞情況傳播延遲

• 從 A_i 或 B_i 到 C_i+1：4 門延遲（異或 → 與 → 或）
• 從 A_i 或 B_i 到 S_i：4 門延遲（異或 → 異或）
• 從 C_i 到 C_i+1：2 門延遲（與 → 或）
• 從 C_i 到 S_i：2 門延遲（異或）

因為一級門的進位輸出是下一級的輸入，所以最壞情況傳播延遲是

• 從生成第一個進位訊號（A₀/B₀ → C₁）開始的 4 門延遲。
• 每個中間階段（C_i → C_i+1）的 2 門延遲。
• 在最後一個階段產生和和進位輸出（C_n-1 → C_n 和 S_n-1）的 2 門延遲。

因此，對於一個 n 位加法器，我們有一個總傳播延遲，t_p 為

$t_{p}=4+2(n-2)+2=2n+2$

這與 n 成線性關係，對於一個 32 位數，需要 66 個週期才能完成計算。這相當慢，並且在一定程度上限制了我們裝置的字長。我們想要找到加速它的方法。

先行進位加法器

一種快速加數的方法稱為先行進位。這種方法不需要進位訊號逐級傳播，從而造成瓶頸。相反，它使用額外的邏輯來加速進位資訊的傳播和生成，以更少的硬體成本實現快速加法。

在行波加法器中，每個階段都會比較進位輸入訊號，C_i，與輸入 A_i 和 B_i，並相應地生成進位輸出訊號 C_i+1。在先行進位加法器中，我們定義了兩個新的函式。

生成函式，G_i，指示如果不存在進位輸入訊號，該階段是否會生成進位輸出訊號 C_i。如果兩個加數在該位上都包含 1，則會發生這種情況

$G_{i}=A_{i}\cdot B_{i}\,$

傳播函式，P_i，指示是否將該階段的進位輸入傳遞到該階段的進位輸出。如果兩個加數中的任何一個在該位上包含 1，則會發生這種情況

$P_{i}=A_{i}+B_{i}\,$

請注意，這兩個值都可以在單個門延遲的恆定時間內從輸入中計算出來。現在，如果該階段生成進位（G_i = 1）或存在進位輸入並且該階段傳播進位（P_i·C_i = 1），則該階段的進位輸出發生

$C_{i+1}=A_{i}B_{i}+A_{i}C_{i}+B_{i}C_{i}\,$

$C_{i+1}=A_{i}B_{i}+(A_{i}+B_{i})C_{i}\,$

$C_{i+1}=G_{i}+P_{i}C_{i}\,$

下表總結了這一點

Ai	Bi	Ci		Gi	Pi	Ci+1
0	0	0		0	0	0
0	0	1		0	0	0
0	1	0		0	1	0
0	1	1		0	1	1
1	0	0		0	1	0
1	0	1		0	1	1
1	1	0		1	1	1
1	1	1		1	1	1

我們可以透過代入前一級的進位表示式來擴充套件進位表示式

$c_{i+1}=G_{i}+P_{i}c_{i}\,$

$c_{i+1}=G_{i}+P_{i}\left(G_{i-1}+P_{i-1}c_{i-1}\right)\,$

$c_{i+1}=G_{i}+P_{i}G_{i-1}+P_{i}P_{i-1}\left(G_{i-2}+P_{i-2}c_{i-2}\right)\,$

$c_{i+1}=\quad \vdots$

$c_{i+1}=G_{i}+P_{i}G_{i-1}+P_{i}P_{i-1}G_{i-2}+P_{i}P_{i-1}P_{i-2}G_{i-3}+\ldots +P_{i}P_{i-1}\cdots P_{1}P_{0}c_{0}\,$

注意，這不需要來自先前級的進位訊號，因此我們不必等待更改在電路中級聯傳播。事實上，一旦傳播和生成訊號準備就緒，給定級的進位訊號就可以用另外兩個門延遲（一個與門和一個或門）計算出來。因此，給定級的進位可以在恆定時間內計算出來，因此和也可以在恆定時間內計算出來。

操作	所需資料	門延遲
生成級生成和傳播訊號	加數 (a 和 b)	1
生成級進位訊號，C1 到 Cn	P 和 G 訊號，以及 C0	2
生成和結果，S	進位訊號和加數	3
總計		6

S、P 和 G 訊號均由稱為“部分全加器”（PFA）的電路生成，該電路類似於全加器。

請注意，雖然在上面的電路圖中，P 訊號被生成為了 A OR B，但另一個有效的選擇是 A XOR B，優勢在於 A XOR B 已經在電路圖中出現，不需要額外的門。這是因為在公式 $C_{i+1}=G_{i}+P_{i}C_{i}$ 中，$P_{i}$ 的實現方式並不重要，因為 $AB+(A+B)C$ 和 $AB+(A\oplus B)C$ 是等效的表示式，讀者可以使用真值表進行驗證。

為了構建一個稍微小一點的電路，傳播訊號可以從第一個 XOR 門的輸出端獲取，而不是使用專門的 OR 門，因為如果 A 和 B 都被斷言，生成訊號將強制產生進位。然而，這種簡化意味著傳播訊號需要兩個門延遲才能產生，而不僅僅是一個門延遲。

進位超前加法器包含 n 個 PFA 和用於從級傳播和生成訊號產生進位的邏輯。

因此，兩個數字可以在恆定時間內加起來，即 O(1)，只需要 6 個門延遲，與數字的長度 n 無關。然而，這需要具有高達 n 個輸入的 AND 和 OR 門。如果邏輯閘只有有限數量的輸入，則需要構建樹來計算這些輸入，而總的計算時間是對數的，即 O(ln(n))，這仍然比波紋加法器的線性時間好得多。

級聯進位超前加法器

基本進位超前加法器速度非常快，但缺點是它需要大量的邏輯硬體來實現。事實上，所需的硬體量大約與 n 的平方成正比，並且當 n 大於 4 時開始變得非常複雜。

因此，大多數 CLA 由包含 4 位 CLA 的“塊”構成，這些塊被級聯起來以產生更大的 CLA。

進位保留加法器

進位保留加法器是一種傳播延遲（關鍵路徑）較低的加法器，但它不是將兩個輸入數字加到一個輸出和，而是將三個輸入數字加到一對輸出數字。當它的兩個輸出然後被一個傳統的進位超前加法器或波紋進位加法器相加時，我們得到所有三個輸入的和。

在將三個或更多個數字加在一起時，以單個進位超前加法器結尾的一系列進位保留加法器比一系列進位超前加法器提供了更好的傳播延遲。特別是，進位保留加法器的傳播延遲不受被加向量的寬度影響。

進位保留加法器實際上是完全並行的全加器電路陣列，三個輸入向量的每個位都載入到每個全加器的 A、B 和 Cin 輸入。每個全加器的輸出 S 連線到一個輸出的相應輸出位，它的輸出 Cout 連線到第二個輸出的下一個更高的輸出位；第二個輸出的最低位直接從進位保留的 Cin 輸入饋送。

本節的 數位電路 華夏公益教科書是一個 存根。您可以透過擴充套件本節來幫助我們。如果您添加了一些內容，請將自己列為 貢獻者。