數位電路/CORDIC

一個 CORDIC (代表 **CO**ordinate **R**otation **DI**gital **C**omputer) 電路用於計算一些常見的數學函式，例如三角函式、雙曲函式、對數函式和指數函式。

應用

CORDIC 只使用加法器和位移來計算結果，因此它可以使用相對基本的硬體實現。

像冪級數或查表法通常需要執行乘法。如果硬體乘法器不可用，CORDIC 通常更快，但如果可以使用乘法器，其他方法可能更快。

CORDIC 可以用多種方法實現，包括單級迭代方法，與乘法器電路相比，它需要很少的門。此外，CORDIC 可以使用完全相同的硬體計算許多函式，因此它們非常適合那些將降低成本（例如透過減少 FPGA 中的門數）優先於速度的應用。這種優先順序的一個例子是袖珍計算器，其中 CORDIC 被廣泛使用。

歷史

CORDIC 最初是由 J.E. Volder 於 1959 年在康維爾航空電子部門發明的，它被設計用於 B-58 轟炸機的導航計算機，以取代模擬分解器，一種計算三角函式的裝置（圓 CORDIC）。

1971 年，惠普的 J.S. Walther 將該方法擴充套件到計算雙曲函式、自然對數、自然指數、乘法、除法和平方根（線性 CORDIC 和雙曲 CORDIC）。

2019 年，基於雙曲 CORDIC，羅元勇等人進一步提出了一種廣義雙曲 CORDIC (GH CORDIC) 來直接計算具有任意固定基數的對數和指數。理論上，雙曲 CORDIC 是 GH CORDIC 的特例。

通用概念

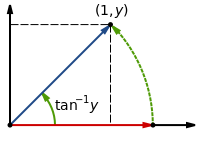
考慮以下向量的旋轉

從 (1, 0) 開始 旋轉 θ 我們得到 (cosθ, sinθ)	從 (1, y) 開始 旋轉直到 y = 0 旋轉是 tan−1y

如果我們有一個計算效率高的向量旋轉方法，我們可以直接計算正弦、餘弦和反正切函式。但是，任意角度的旋轉並不容易（你必須知道正弦和餘弦，而這正是我們所沒有的）。我們使用兩種方法來簡化它

• 我們不執行旋轉，而是執行“偽旋轉”，它們更容易計算。
• 用一組特殊角度 α_i 的和來構造所需的角度 θ

$\theta =\alpha _{1}+\alpha _{2}+\ldots +\alpha _{m}$

下圖顯示了長度為 R_i 的向量繞原點旋轉 a_i 角的旋轉和偽旋轉

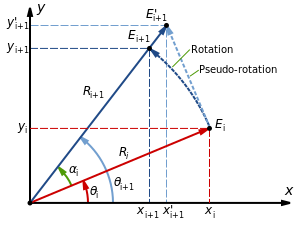
繞原點旋轉產生以下座標

$x_{i+1}=x_{i}\cos \alpha _{i}-y_{i}\sin \alpha _{i}$

$y_{i+1}=y_{i}\cos \alpha _{i}+x_{i}\sin \alpha _{i}$

$\theta _{i+1}=\theta _{i}+\alpha _{i}$

回想一下身份 $\cos \theta \equiv 1{\Big /}{\sqrt {1+\tan ^{2}\theta }}$.

$x_{i+1}=\left(x_{i}-y_{i}\tan \alpha _{i}\right){\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

$y_{i+1}=\left(y_{i}+x_{i}\tan \alpha _{i}\right){\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

我們的策略是消除因子 $1{\Big /}{\sqrt {1+\tan ^{2}\alpha _{i}}}$，並設法消除乘以 $\tan \alpha _{i}$。偽旋轉生成一個與旋轉向量具有相同角度但長度不同的向量。事實上，偽旋轉將長度更改為

$R_{i+1}={\frac {R_{i}}{\cos \alpha _{i}}}=R_{i}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

因此，我們現在有以下偽旋轉後的座標

$x_{i+1}^{\prime }=\left(x_{i}-y_{i}\tan \alpha _{i}\right)$

$y_{i+1}^{\prime }=\left(y_{i}-x_{i}\tan \alpha _{i}\right)$

$\theta _{i+1}=\theta _{i}-\alpha _{i}$

偽旋轉成功地消除了我們的長度因子，而長度因子本來需要一個代價高昂的除法運算。然而，向量將在n個偽旋轉序列中增長K倍

$K=\prod _{i=0}^{n-1}{\sqrt {1+\tan ^{2}\alpha _{i}}}$

然後，經過n個偽旋轉後的座標為

$x_{n}=K\left(x_{i}\cos \sum _{i=0}^{n-1}{\alpha _{i}}-y_{i}\sin \sum _{i=0}^{n-1}\alpha _{i}\right)$

$y_{n}=K\left(y_{i}\cos \sum _{i=0}^{n-1}{\alpha _{i}}+x_{i}\sin \sum _{i=0}^{n-1}\alpha _{i}\right)$

$\theta _{n}=\theta _{i}-\sum _{i=0}^{n-1}{\alpha _{i}}$

前三次偽旋轉。注意我們如何收斂到正確的角度，θ

如果角度總是相同的集合，那麼 K 是固定的，可以在以後考慮。我們根據兩個標準選擇這些角度

• 我們還必須選擇角度，以便任何角度都可以透過所有角度的總和來構建，並帶有適當的符號。
• 我們將所有 $\tan \alpha _{i}$ 設定為 2 的冪，以便乘法可以透過二進位制數的簡單邏輯移位來執行。

正切函式在區間 [0, π/2] 上具有單調遞增的梯度，因此給定角度的正切始終小於該角度的一半正切的兩倍。這意味著如果我們使角度 $\alpha _{i}=\tan ^{-1}2^{-i}$，我們可以滿足這兩個標準。請注意，正切函式是奇函式，這意味著要以另一種方式進行偽旋轉，您只需減去而不是新增角度的正切。

i	αi = tan−1 (2−i)
	度	弧度
0	45.00	0.7854
1	26.57	0.4636
2	14.04	0.2450
3	7.13	0.1244
4	3.58	0.0624
5	1.79	0.0312
6	0.90	0.0160
7	0.45	0.0080
8	0.22	0.0040
9	0.11	0.0020

在過程的步驟 i 中，我們以 $d_{i}2^{-i}\,$ 進行偽旋轉，其中 $d_{i}\,$ 是旋轉的方向（或符號），這將在每一步都選擇，以迫使角度收斂到所需的最終旋轉。例如，考慮 28° 的旋轉

$28\approx 45.0-26.57+14.04-7.13+3.58-1.79+0.90-0.45+0.22+0.11$

$28\approx 27.91$

我們採取的步驟越多，我們就可以透過連續旋轉來進行更好的近似。因此，我們有以下迭代座標計算

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$\theta _{i+1}=\theta _{i}-d_{i}\alpha _{i}$

為了達到k位的精度，需要進行k次迭代，因為$\tan ^{-1}2^{-i}\lessapprox 2^{-i}$，隨著i的增加而收斂。

使用CORDICs

CORDICs可以用來計算許多函式。一個CORDIC有三個輸入，x₀, y₀和z₀。根據CORDIC的輸入，可以在輸出x_n, y_n和z_n產生不同的結果。

在旋轉模式下使用CORDIC

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$ $y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$ $z_{i+1}=z_{i}-d_{i}\alpha _{i}$

$x_{n}=K\left(x_{0}\cos z_{0}-y_{0}\sin z_{0}\right)$ $y_{n}=K\left(y_{0}\cos z_{0}+x_{0}\sin z_{0}\right)$ $z_{n}=0$

為了使z_n收斂到0，選擇$d_{i}={\mbox{sgn }}z_{i}$.

如果我們從x₀ = 1/K和y₀=0開始，在過程結束時，我們會發現x_n=cos z₀和y_n=sin z₀。

收斂域是$-99.7^{\circ }<z_{0}<99.7^{\circ }$，因為99.7°是列表中所有角度的總和。

在向量模式下使用CORDIC

$x_{i+1}=x_{i}-d_{i}y_{i}2^{-i}$ $y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$ $z_{i+1}=z_{i}-d_{i}\alpha _{i}$

$x_{n}=K{\sqrt {x^{2}+y^{2}}}$ $y_{n}=0$ $z_{n}=z_{0}+\tan ^{-1}\left(y_{0}/x_{0}\right)$

為了使y_n收斂到0，選擇$d_{i}=-{\mbox{sgn }}(y_{i})$.

如果我們從x₀ = 1和z₀ = 0開始，我們會發現z_n=tan⁻¹y₀

CORDICs的實現

位並行，展開

位並行，迭代

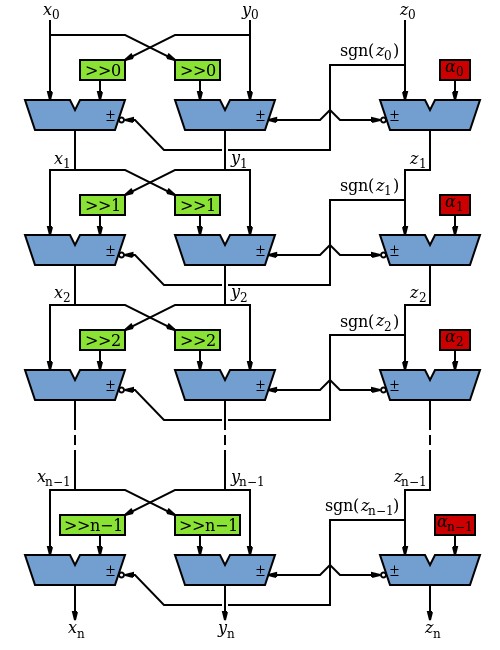
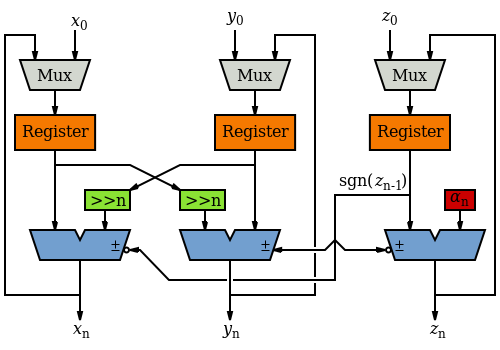
如果不需要高速，可以使用一個加法器和一個移位器實現。

通用 CORDIC

透過引入因子μ，我們也可以滿足線性函式和雙曲函式的需求。

$x_{i+1}=x_{i}-\mu d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$z_{i+1}=z_{i}-d_{i}\alpha _{i}$

通用 CORDIC 實現的總結

$x_{i+1}=x_{i}-\mu d_{i}y_{i}2^{-i}$

$y_{i+1}=y_{i}+d_{i}x_{i}2^{-i}$

$z_{i+1}=z_{i}-d_{i}\alpha _{i}$

模式	旋轉	向量化
	$d_{i}={\mbox{sgn }}(z_{i}),\quad z\rightarrow 0$	$d_{i}=-{\mbox{sgn }}(y_{i}),\quad y\rightarrow 0$
圓形 μ = 1 αi = tan−12−i
線性 μ = 0 αi = 2−i
雙曲 μ = -1 αi = tanh−12−i
在雙曲模式下，需要重複第 4，13，40，121，...，j，3j+1，... 步。下面的常數K' 可以解釋這一點。 K = 1.646760258121... 1/K = 0.607252935009... K' = 0.8281593609602... 1/K' = 1.207497067763...

直接可計算函式

$\sin z\,$	$\cos z\,$
$\tan ^{-1}z\,$	$\sinh z\,$
$\cosh z\,$	$\tanh ^{-1}z\,$
$y/x$	$xz$
$\tan ^{-1}(y/x)\,$	${\sqrt {x^{2}+y^{2}}}$
${\sqrt {x^{2}-y^{2}}}$	$e^{z}=\sinh z+\cosh z$

間接可計算函式

除了上述函式外，還可以透過組合先前計算結果來生成許多其他函式。

$\tan z={\frac {\sin z}{\cos z}}\,$	$\cos ^{-1}w=\tan ^{-1}{\frac {\sqrt {1-w^{2}}}{w}}$
$\tanh z={\frac {\sinh z}{\cosh z}}$	$\sin ^{-1}w=\tan ^{-1}{\frac {w}{\sqrt {1-w^{2}}}}$
$\ln w=2\tanh ^{-1}{\frac {w-1}{w+1}}$	$\log _{b}w={\ln w \over \ln b}$
$w^{t}=e^{t\ln w}$	$\cosh ^{-1}=\ln \left(w+{\sqrt {w^{2}-1}}\right)$
$\tan ^{-1}(y/x)\,$	$\sinh ^{-1}=\ln \left(w+{\sqrt {w^{2}+1}}\right)$
${\sqrt {x^{2}-y^{2}}}$	${\sqrt {w}}={\sqrt {(w+1/4)^{2}-(w-1/4)^{2}}}$

進一步閱讀

• Volder, J.E. (1959), "CORDIC 三角函式計算技術" (PDF), IRE 電子計算機學報, 8 (3): 330–334, 檢索於 2009-06-02
• Walther, J.S. (1971), "基本函式的統一演算法" (w), 1971 年 5 月 18 日至 20 日春季聯合計算機大會論文集: 379–385, 檢索於 2009-06-02
• 羅元勇，王雨軒，哈亞軍，王忠鋒，陳思遠，潘洪兵 (2019)，"廣義雙曲 CORDIC 及其任意固定基數的對數和指數計算"，IEEE 超大規模積體電路 (VLSI) 系統彙刊，27 (9): 2156–2169，doi:10.1109/TVLSI.2019.2919557 {{citation}}: |access-date= requires |url= (help)CS1 maint: multiple names: authors list (link)
• Vladimir Baykov，基於逐位 (CORDIC) 技術的基本函式評估問題，博士論文，列寧格勒國立電氣工程大學，1972 年
• Schmid, Hermann，十進位制計算。紐約，Wiley，1974 年
• V.D.Baykov，V.B.Smolov，計算機中基本函式的硬體實現，列寧格勒國立大學，1975 年，96 頁。*全文
• Senzig, Don，計算器演算法，IEEE Compcon 閱讀摘要，IEEE 目錄號 75 CH 0920-9C，第 139-141 頁，IEEE，1975 年。
• V.D.Baykov，S.A.Seljutin，微型計算器中的基本函式評估，莫斯科，Radio & svjaz，1982 年，64 頁。
• Vladimir D.Baykov，Vladimir B.Smolov，專用處理器：迭代演算法和結構，莫斯科，Radio & svjaz，1985 年，288 頁
• M. E. Frerking，通訊系統中的數字訊號處理，1994 年
• Vitit Kantabutra，關於計算指數和三角函式的硬體，IEEE 計算機彙刊 45 (3)，328-339 (1996)
• Andraka, Ray，基於 FPGA 計算機的 CORDIC 演算法調查
• Henry Briggs，對數算術。倫敦，1624 年，對開本
• CORDIC 文獻網站，王少雲，2011 年 7 月
• 演算法的秘密，Jacques Laporte，巴黎 1981 年
• 逐位方法，Jacques Laporte，巴黎 2006 年
• Ayan Banerjee，基於 CORDIC 的生物醫學訊號處理 FFT 處理器的 FPGA 實現，卡拉格浦爾，2001 年
• CORDIC 架構：綜述，B. Lakshmi 和 A. S. Dhar，期刊：VLSI 設計，2010 年 1 月
• 在數字下變頻器中實現 CORDIC 演算法，C. Cockrum，2008 年秋季
• Parhami, B. (1999)，計算機算術：演算法和硬體設計