電和磁/靜電學

僅僅透過摩擦不同的材料，比如頭髮和塑膠，就可以產生電力。這會在兩個摩擦的表面上產生大小相等但符號相反的電荷。然後我們可以觀察到符號相反的電荷之間的吸引力和符號相同的電荷之間的排斥力。

庫侖定律

兩個靜止的電荷之間施加的電力與其電荷乘積成正比，與其距離的平方成反比。這兩個力，即 A 對 B 施加的力和 B 對 A 施加的力，都位於連線 A 和 B 中心線的方向上。這兩個力在電荷符號相反時是吸引力，在電荷符號相同時是排斥力。

場是一個在空間中每個點每個時刻都可能變化的物理量。例如，溫度就是一個場。庫侖定律指出，一個靜止的電荷 $q$ 會永久地在空間中產生一個電力場 $\mathbf {E}$

$\mathbf {E} (\mathbf {r} )=k_{e}{\frac {q}{r^{2}}}\mathbf {\hat {r}}$

其中 $\mathbf {r}$ 是從電荷 $q$ 到所考慮點的向量，$r$ 是它的長度，$\mathbf {\hat {r}} =\mathbf {r} /r$ 是 $\mathbf {r}$ 方向上的單位長度向量，$k_{e}={\frac {1}{4\pi \epsilon _{0}}}$ 是一個取決於測量單位選擇的常數。

電力場 $\mathbf {E}$ 對電荷 $q'$ 施加的力是 $\mathbf {F} =q'\mathbf {E}$

所以電荷 $q$ 對電荷 $q'$ 的作用力是 ${\frac {1}{4\pi \epsilon _{0}}}{\frac {qq'}{r^{2}}}\mathbf {\hat {r}}$

場 $\mathbf {E}$ 就像一個計算一個電荷對另一個電荷作用力的數學中間量。但它遠不止一個簡單的數學中間量。它擁有獨立存在的意義。麥克斯韋證明光是一種電磁波，即電磁場 ($\mathbf {E}$, $\mathbf {B}$) 的傳播運動，而電場 $\mathbf {E}$ 是其中一個組成部分。

帶正電球體表面的電場

兩個電荷對第三個電荷的作用力是它們分別施加的作用力的總和。宇宙中所有電荷共同在空間中產生一個電場，它是每個電荷分別產生的電場的總和。

庫侖力在數學上與萬有引力相似：兩個物體之間相互作用的萬有引力與它們的質量乘積成正比，與它們之間距離的平方成反比。但萬有引力總是吸引力，因為不存在負質量。在地球上，物體的重量就是地球對它的萬有引力。

根據相對論，不存在瞬時超距作用。因此，一個電荷不能瞬時對另一個電荷施加庫侖力。必須考慮力的傳播時間。這就是為什麼庫侖定律只是靜電學定律。它允許我們正確計算靜止電荷之間的力。

物質的凝聚是靜電性的

一粒小小的鹽

每條線代表 NaCl 晶體中兩個離子之間的鍵（氯化鈉是食鹽）。藍色和綠色代表兩種離子。它是一個體心立方晶體。每個 Na⁺ 離子周圍有 8 個最近的 Cl^- 離子。同樣，每個 Cl^- 離子周圍有 8 個最近的 Na⁺ 離子。兩個相鄰離子總是帶相反的電荷，因為異性電荷相互吸引，而同性電荷相互排斥。

解釋固體、原子和分子凝聚力的力是庫侖力。液體的凝聚也部分是由這種靜電力引起的，但由於原子或分子在運動，因此電動力也可以起作用。

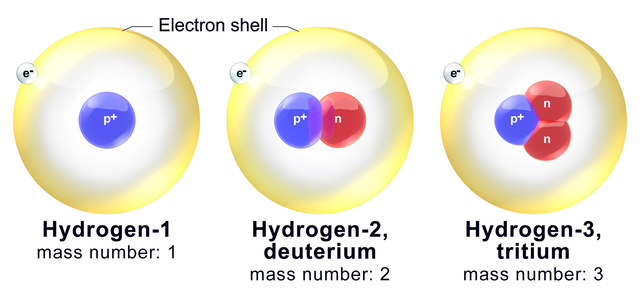
氫原子由一個質子、零個、一個或兩個中子和一個電子組成。質子帶正電。電子帶負電，大小相等，符號相反。中子是中性的。電子透過庫侖電力與質子相連。更一般地說，原子由一個原子核和核外電子組成。原子核的電荷為正，大小相等，符號相反於電子的總電荷。

當氫原子處於基態，即最低能量狀態時，電子圍繞質子的存在類似於一個球形雲。

質子位於中心。周圍的雲代表電子的存在。

如果原子被激發，電子的存在可以有各種形式。

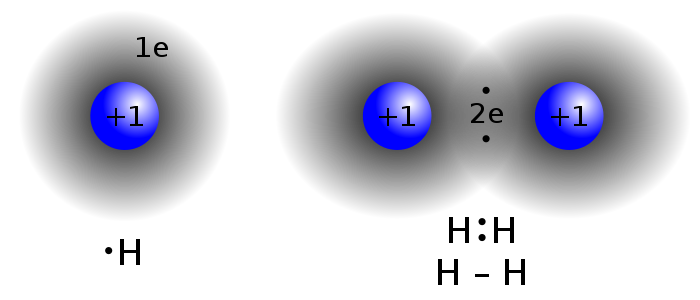
分子是原子組成的集合。電子就像將原子核粘合在一起的膠水。兩個正電荷相互排斥，但兩個正電荷被一個負電荷隔開可以相互吸引。

離子是指失去或獲得一個或多個電子的原子或分子。由於原子和分子總是電中性的，因此離子總是帶電的。失去一個或多個電子的原子或分子稱為陰離子。獲得一個或多個電子的原子或分子稱為陽離子。

固體是由原子、分子或離子組成的集合，它們透過靜電力相互連線。

要破壞離子晶體，必須分離由靜電力吸引的離子。

異性電荷之間的吸引力大於同性電荷之間的排斥力。這種差異使所有材料具有凝聚力。

原子核的質量大約是伴隨它的電子的 5000 倍，因為質子或中子的質量大約是電子的 2000 倍，而且原子總是具有相同數量的質子和電子，以及數量大約等於或略大於質子數的中子（普通氫除外，它沒有中子）。由於幾乎所有的質量都由原子核（由質子和中子構成）承擔，因此說電子是將原子核粘合在一起的膠水，而不是說原子核是將電子粘合在一起的膠水，更自然。

兩個異性點電荷應該相互吸引，直到它們相遇。我們可以計算出它們以這種方式相互落下時可能提供的能量是無限的。但物質通常不會坍縮，並且它永遠不會釋放無限的能量。物體總是具有更低的能量狀態，即它們的基態。在這種狀態下，它們不能釋放能量，因為它們沒有更低的能量狀態可以進入。原子、分子和離子處於基態或具有較高能量的激發態。氣體越熱，它的原子或分子就越激發。固體處於激發態，除非它的絕對溫度為零開爾文。

要解釋為什麼氫原子中的電子不會落到質子上，或者更一般地說為什麼材料不會坍縮，庫侖定律是不夠的，我們需要量子物理。

什麼是電勢差？

在穩態下，電勢差是兩點之間的電勢差。它的測量單位是伏特 (V)。

什麼是勢？

要理解勢，我們必須理解力的功。

我們可以用與理解重力勢能相同的方式來理解電勢。

我們可以毫不費力地將重物在冰面上移動，因為我們不必對抗重力。另一方面，垂直提起重物需要很大的努力，因為我們必須克服重力。在第一種情況下，重力不做功，因為運動是水平的。在第二種情況下，重力做功，因為運動是垂直的。

力 f 對直線運動的物體在長度 d 上所做的功 W 等於力向量 f 和位移向量 d 的標量積

W = f.d = f d cos $\theta$

其中 $\theta$ 是力向量 f 和位移向量 d 之間的夾角。f 和 d 是向量 f 和 d 的長度。

重力的方向是垂直的。它對水平位移不起作用，因為 cos 90° = 0。重力 $m\mathbf {g}$ 對質量 $m$ 所做的功為

$W=-mgh$

力的功就是能量。如果 $\theta$ > 90°，則 cos $\theta$ < 0，W < 0。力的功值為負，因為它是物體在力的作用下做功而損失的能量。這種能量損失可以是動能 E = 1/2 mv²。速度 v 降低，因為物體受到力的阻礙。如果 $\theta$ < 90°，則 cos $\theta$ > 0，W > 0。力的功值為正，因為它是物體在力的推動下加速運動而獲得的能量。

在國際單位制（MKSA，米、千克、秒、安培）中，能量的單位是焦耳（J）。一焦耳是將物體在一牛頓（N）的力作用下移動一米所需的功。

1 J = 1 N. 1 m = 1 N.m

地球表面的重力約為 9.8 牛頓，幾乎為 10 牛頓。因此，一焦耳大約是將一個 1 公斤的物體舉高十釐米所需的能量。

當物體的軌跡為曲線時，我們透過在遵循曲線軌跡的折線上進行推理來計算力的功。如果線段的長度越來越短，折線就越來越接近它所遵循的曲線。我們透過取各線段上功的總和的極限來求力的功，當線段的長度趨於零時。力的功是力與位移向量在路徑上的標量積的積分。

根據標量積的定義，重力 g 對斜線段 AB 所做的功等於 g(h_A - h_B)，其中 h_A - h_B 是其兩端的高度差。現在，A 和 C 之間的高度差等於 A 和 B 之間的高度差與 B 和 C 之間的高度差之和

h_A - h_C = (h_A - h_B) + (h_B - h_C)

因此，重力 g 對任何從 A 到 Z 的路徑所做的功始終等於 g(h_A - h_Z)。它只取決於端點 A 和 Z 的高度差，而與連線 A 和 Z 的路徑無關。因此，我們在地球表面重力場的情況下證明了

定理：重力的功與所走的路徑無關。

如果我們忽略摩擦力，則過山車上物體的動能就是從靜止開始時重力的功。它只取決於高度差 $h$，而與所走的路徑無關

力的功可能取決於所走的路徑。例如，摩擦力的功隨所走的路徑越長而越大。

當一個力場使得力在兩點之間的功與所走的路徑無關時，我們可以引入一個勢能。它的定義是選擇一個零勢能點。然後，空間中每個點的勢能由力對一個標準物體從該點到零勢能點所做的功來定義。對於重力，我們以質量為一的物體作為標準。對於電力，標準是電荷為一的物體。勢能是明確定義的，因為力的功與所走的路徑無關。

設 W_XY 是力對從 X 移動到 Y 的單位物體所做的功，V_X 是 X 點的勢能，O 是零勢能點。根據 V 的定義，V_A = W_AO，V_B = W_BO。所以 V_A - V_B = W_AO - W_BO。或者 W_AO = W_AB + W_BO。所以 V_A - V_B = W_AB。因此，兩點之間的勢能差始終等於力對從這兩點之間移動的單位物體所做的功。

兩點之間的電壓是電力對從這兩點之間移動的單位電荷所做的功。在穩態下，電力的功與所走的路徑無關，因此這種力來自勢能。電壓就是勢能差。它對於電力來說就像高度差對於重力一樣。

電荷的單位是庫侖。一伏特 (V) 是每庫侖 (C) 一焦耳 (J)。這是給一個庫侖的電荷一焦耳的能量所需的電壓差。

1 V = 1 J/C

當在金屬導線上施加電壓時，電流透過導線，這是電子流。電子被電力加速，但它們的平均動能不會增加，因為它們被金屬減速。它們透過焦耳效應將獲得的所有能量損失給金屬，從而使金屬發熱。電燈泡是透過將承載電流的金屬絲加熱到白熾狀態而發明的。材料的電阻衡量其減緩透過它的電子或離子的能力。

勢能

質量為 $m$ 的物體的重力勢能等於 $mV_{X}$，其中 $V_{X}$ 是點 $X$ 的重力勢。當物體靜止時，它的能量不可見，不實際，因為它的動能為零。當靜止的物體被釋放到自由落體時，它的重力勢能轉化為動能。當物體靜止時，能量已經存在，但它沒有表現出來，它只是潛在的。它轉化為動能是潛能的實現。

對於一個從靜止狀態釋放的自由落體，其運動結束時的動能是其重力勢能的實際體現，最初是不可見的。它等於重力所做的功。所以力的功是潛能的實現。勢能是使力做功的潛力。當我們有可以用來做功的力時，我們就擁有潛能。

能量有許多形式：動能 ${\frac {1}{2}}mv^{2}$ 是質量 $m$ 由於其速度 $v$ 所具有的能量。熱是原子和分子的動能。重力能、電能和核能分別是取決於重力、電和核力的勢能。化學能是原子和分子的電能。光能是光粒子（光子）的動能。

動能方程 $E={\frac {1}{2}}mv^{2}$ 只是一個近似值。根據愛因斯坦的理論，相對論計算給出了更精確的結果。

重力勢能轉化為動能是能量守恆的一個例子。能量永遠不會消失。當一個物體失去能量時，它總是把它傳遞給另一個物體，或者把它轉化為另一種形式的能量。水力發電大壩將重力能轉化為電能。電烤箱將電能轉化為熱能。核電站將核能轉化為熱能，再將熱能轉化為電能。所有形式的能源生產或消耗都是如此。宇宙中的總能量是恆定的。

質量的勢能：E = mc²

即使是質量也是勢能。

任何物體的質量 $m$ 與它被湮滅時可能釋放的能量 $E$ 成正比

$m={\frac {E}{c^{2}}}$

或者

$E=mc^{2}$

其中 $c$ 是光速。

質量總是具有被湮滅的潛力。

方程 $E=mc^{2}$，由愛因斯坦於 1905 年發現，可以從電磁學的基本方程（麥克斯韋方程組）中推匯出，麥克斯韋方程組於 1865 年被發現。它在本書最後一章中得到了解釋和證明。

勢的梯度

當力的功不依賴於所走的路徑時，我們說力場來自一個勢，因為我們可以透過對勢取梯度來計算力。

要理解梯度的概念，最簡單的方法是想象一座山的起伏。山坡上某一點的高度 h(x,y) 相對於海平面上的點 (x,y) 的高度是一個標量場。我們可以稱它為高度場。從這個標量場我們可以定義一個向量場。對於每個點 (x,y)，我們定義一個向量 v(x,y)，其方向是該點山坡的最大傾斜線，方向向上，其長度是最大傾斜線的斜率（如果我們水平移動 100 米時上升了 10 米，則斜率等於 10% = 10/100 = 0.1）。這樣定義的向量場就是高度場的梯度：v = grad h

在這些影像中，標量場用灰色陰影表示。它的梯度用箭頭表示。如果標量場表示地形的起伏，第一個表示一個圓錐，第二個表示一個傾斜平面。

等高線是指等高線。如果 h 是一個勢能，我們稱它們為等勢線。

最大傾斜線是指始終沿著最大傾斜方向延伸的線。它們始終在每個點都與向量場相切。如果 h 是一個勢能，我們稱它們為場線。

最大傾斜線始終垂直於等高線。同樣，場線始終垂直於等勢線。

黑線是場線，棕線是兩個等量異號電荷產生的電場的等勢線。

在地形圖上，相鄰的等高線始終表示相同的差值。它們越緊密，斜率越大。如果以同樣的方式繪製相同電位差的相鄰等勢線，則線越緊密，場越大。

• 
• 

對於二維空間中的標量場 $h$，我們可以透過求其兩個偏導數來計算其梯度。grad $h$ 的分量為 $\partial h/\partial x$ 和 $\partial h/\partial y$。

三維空間中標量場 $V$ 的梯度 grad $V$ 是一個向量場，其分量為 $\partial V/\partial x$，$\partial V/\partial y$ 和 $\partial V/\partial z$。

根據勢能的定義，如果我們將標準物體移動 dx 的距離，其勢能變化為 dV = -f_x dx，其中 f_x 是力 f 在 x 方向上的分量。因此 f_x = $-\partial V/\partial x$。類似地，f_y = $-\partial V/\partial y$ 和 f_z = - $\partial V/\partial z$。

作用在標準物體上的力 f 是勢能 $V$ 梯度的反方向

f = -grad $V$

這是我們從勢能計算力場的通用公式。

電荷產生的庫侖勢能

根據庫侖定律，負電荷 -q 產生的電場 E 是指向電荷中心的向量場，其大小為 q/r²，其中 r 是從該中心到該點的距離。對於正電荷 q，它是相同的場，只是向量方向相反。

電荷 q 產生的電場 E 來自庫侖勢 V = q/r，其中 r 是從電荷中心到該點的距離。

E = -grad V = -grad q/r

等勢面是以電荷為中心的球面。場線都是從電荷中心延伸出來的直線。

該勢能在透過電荷的平面上可以用高度場表示。

等高線是等勢線。它們是等勢球面與透過電荷的平面的交線。

-dV/dr = q/r² = E，如果 q 是正電荷，則向量 E 的長度。

電荷的庫侖勢與質量的萬有引力勢相似。

這些線是地球產生的萬有引力場的場線，即重力場。

多個電荷產生的勢能

多個電荷產生的電場是每個電荷單獨產生的場的總和。現在，一個和的梯度是梯度的總和，因為 d(f+g)/dx = df/dx + dg/dx。因此，多個電荷產生的電場來自每個電荷單獨產生的電勢的總和。因此，我們證明了多個電荷產生的電場也來自一個勢能。由於牛頓勢能與庫侖勢在數學上相似，因此萬有引力也一樣。

產生兩個相等且相反電荷的場可以用場線表示

以及等勢線

或透過將它的勢能表示為一個浮雕

我們也可以在空間中看到場線

地球和月球產生的萬有引力勢與兩個負電荷產生的電勢相同，這兩個負電荷將具有與地球和月球質量成比例的電荷。

場線為藍色，等勢線為紅色。

我們也可以用高度場來表示這個勢能。

電容器的電荷

電容器由兩個導電板組成，彼此非常靠近，並由絕緣材料隔開。每個端子連線到一個板。當電容器開啟時，一個板會失去一些電子而帶正電，而另一個板會獲得電子而帶負電。

我們用高斯定理（在麥克斯韋方程的章節中）證明了無限帶電平面的電場力場 $\mathbf {E}$，其電荷密度是均勻的，等於 $\sigma$，在帶電平面的每一邊也是均勻的，垂直於它，其大小為 $E={\frac {\sigma }{2\epsilon _{0}}}$，如果它被真空包圍，並且它在平面每一邊的方向與其在另一邊的方向相反。

由於多個電荷產生的電場是每個電荷產生的場的總和，因此兩個表面電荷密度相等且相反的平行帶電平面產生的電場在平面之間是均勻的，垂直於它們，其大小為

$E={\frac {\sigma }{\epsilon _{0}}}$

其中 $\sigma$ 是表面電荷密度的絕對值，

而在兩個帶電平面的外部空間中，它等於零。

有限表面電容器產生的場與前一個場相同，只是在邊緣處不同。

電場力對平板之間的一個單位電荷所做的功等於 $Ed$，其中 $d$ 是它們的距離。對於遠離邊緣的完成的板，這仍然是正確的。因此，平板之間的電壓 $V$ 與它們的電荷 $Q$ 成正比。因此，電荷與電壓成正比。

$Q=CV$

其中 $C$ 是電容器的電容。 $C$ 度量了對於給定電壓，一個板接收的電荷量。

$C={\frac {\epsilon _{0}S}{d}}$

對於表面積為$S$的平板，它們之間為真空，相距$d$。

證明：$C=Q/V={\frac {\sigma S}{Ed}}={\frac {\sigma S}{\sigma d/\epsilon _{0}}}={\frac {\epsilon _{0}S}{d}}$

這就是為什麼我們要用表面積大、相互纏繞的導體板來製造電容器，並且用盡可能薄的絕緣薄膜將它們隔開。

$\epsilon _{0}$ 是真空介電常數。

如果平板之間用介電常數為 $\epsilon$ 的絕緣材料隔開，電容器的電容為

$C={\frac {\epsilon S}{d}}$

導電材料的靜電學

當材料中包含可以自由移動的電荷時，該材料就是導電的。在金屬中，這些電荷是導電電子。在半導體中，它們也可以是空穴，即電子海中缺失的電子，它們在電子海中移動。在鹽水等離子溶液中，可移動的電荷是正離子和負離子。

在導電材料內部，靜電場始終為零。

證明：如果場不為零，移動的電荷就會受到電力的作用而移動，場就不會是靜止的。

另一方面，電荷可以積累在導電材料的表面。如果我們將一個金屬物體放置在電荷附近，它的導電電子會移動以完全補償從外部施加到金屬內部的電場。從外部施加的場和積累在表面上的電子施加的場的總和在金屬內部始終等於零。

在導電材料表面的外側，電場垂直於表面。

證明：如果平行於表面的電場分量不為零，表面電荷就會移動以抵消它。

如果表面電荷密度為正，則表面電場從導電材料向外指向。如果它是負的，它就指向內部。

證明：如果相反，電力會將可移動電荷推入材料內部。

電場對錶面電荷施加力，但不能使它們移動，因為它們不能從材料中移出。

在導電材料的表面，電場為

$E={\frac {\sigma }{\epsilon _{0}}}$

其中$\sigma$是表面電荷密度。

證明在麥克斯韋方程一章的關於高斯定理中給出。

電荷總是朝抵消它們運動原因的方向移動。兩個相等且相反的電荷如果完全重疊，就會產生完全為零的電場。當它們相互吸引時，它們會朝抵消它們運動原因的電場的方向移動。

當電容器的端子連線到金屬導線時，導電電子會受到電容器極板上的電荷施加的電力的作用，這會使它們朝放電方向移動，而不是朝電荷增加的方向移動。

電極化

當物體兩點之間出現電荷差時，物體就被電極化了。

導電體在被放置在均勻的外部電場中時會被極化。物體兩側會出現相反的表面電荷。

絕緣體也會被均勻電場極化。兩側會出現表面電荷。這怎麼可能呢，因為根據定義，絕緣體沒有可以自由移動的電荷？

在絕緣體中，電子附著在原子核上。沒有自由導電電子可以從一個原子核轉移到另一個原子核。圍繞它們所附著的原子核，電子保留了一點活動能力。它們可以集中在一邊或另一邊以補償它們所受到的外部電力。我們可以將被困在原子或分子中的電子視為被原子核保留的電液體，可以變形。這就是為什麼絕緣體像導電體一樣可以被電場極化的原因。

在絕緣體內部，當它被均勻的外部場極化時，電荷會均勻地移動。因此，材料內部的電荷密度保持為零。表面電荷密度是唯一變化的。

絕緣體在極化時，正負電荷在絕緣體內部的移動是瞬態電流。但不能在絕緣材料中流動永久電流。

當物體被電極化時，它會朝施加的電力的方向定向

電荷系統的勢能

如何計算電荷系統的電勢能？

一個電荷$q$放置在電勢$V$中，具有電勢能$qV$。

如果我們使用公式$E_{p}=qV$將所有電荷的電勢能加起來，我們得不到正確的結果。為什麼？

為了計算系統的勢能，我們必須計算組裝系統時所消耗或獲得的能量。 當我們組裝電荷時，它們必須穿過的電場在組裝開始和結束時並不相同。 當系統組裝好後我們計算得到的勢能 $V$，它不是電荷組裝時遇到的電場的勢能，它只是當新的電荷被帶到系統附近時，它所遇到的電場的勢能。

第一個組裝的電荷不會遇到任何要被置於其中的電場力場，因為之前沒有電荷存在。 第二個電荷遇到第一個電荷產生的電場。 第三個電荷遇到前兩個電荷產生的電場，以此類推，直到最後一個電荷，它遇到所有先前電荷產生的電場。

示例：帶電電容器的勢能

為了給電容器充電，必須將電子從其一個極板移動到另一個極板。 第一個移動的電荷 $dq$ 沒有遇到電場，因為電容器沒有充電。 因此，移動它所必須做的功 $dW$ 為 $dW=0$。 如果電容器已經由電荷 $q=\int dq$ 充電，新的電荷 $dq$ 會遇到電場力場，因此它的起點和到達點之間存在電勢差 $V_{2}-V_{1}={\frac {q}{C}}$。 所以

$dW=(V_{2}-V_{1})dq={\frac {q}{C}}dq$

$W=\int dW=\int {\frac {q}{C}}dq={\frac {1}{2}}CV^{2}$

$E_{p}={\frac {1}{2}}CV^{2}$ 因此是帶電荷 $Q=CV$ 的電容器的電勢能，其中 $C$ 是它的電容， $V$ 是它兩極板之間的電勢差。

電勢能在哪裡？

電勢能歸因於電荷。 這種能量是由電荷攜帶的嗎？ 它位於電荷上嗎？

$E=mc^{2}$。 質量總是能量。 能量總是具有質量。 本書末尾證明了這個方程，它表明被困在箱子裡的光會增加箱子的質量。 因此，光具有與其能量除以 $c^{2}$ 相等的質量。

如果電勢能侷限於電荷上，它們能量的變化會導致它們的質量變化。 但是，這種效應從未被觀察到。

電荷系統的電勢能存在於它們產生電場的整個空間中，它是由電場攜帶的。 靜電場 $\mathbf {E}$ 中的電能體積密度為

${\frac {dE_{p}}{dV}}={\frac {1}{2}}\epsilon _{0}\mathbf {E} ^{2}$

其中 $dE_{p}$ 是一個微小體積 $dV$ 內包含的電勢能。

當我們將兩個同種電荷靠近時，我們增加了電場的能量。

如果我們將兩個異種電荷靠近，我們降低了電場的能量。原子核中質子和中子結合在一起的核力也是如此。我們要提供能量才能將它們分開。這就是為什麼它們分離時質量比結合時更大的原因。

將構成質子或中子的三個夸克完全分開需要無限的能量。這就是為什麼我們永遠無法觀察到孤立的夸克。

讓我們證明 ${\frac {dE_{p}}{dV}}={\frac {1}{2}}\epsilon _{0}\mathbf {E} ^{2}$ 允許我們正確地計算帶電電容器的電勢能。

$E_{p}=\int _{V}dE_{p}=\int _{V}\epsilon _{0}\mathbf {E} ^{2}dV={\frac {Sd\sigma ^{2}}{2\epsilon _{0}}}$

其中 $S$ 是電容器的表面積，$d$ 是兩極板之間的距離，$Sd$ 是兩極板之間的體積，${\frac {\sigma }{\epsilon _{0}}}$ 是表面電荷密度 $\sigma$ 產生的電場 $E$。

現在

$C={\frac {\epsilon _{0}S}{d}}$$C={\frac {\epsilon _{0}S}{d}}$ 並且 $V=Ed={\frac {\sigma d}{\epsilon _{0}}}$

所以

$E_{p}={\frac {1}{2}}CV^{2}$

當我們定義電勢時，我們可以自由選擇零電勢點。為了計算電場力，任何選擇都是合適的，因為兩個電勢相差一個常數具有相同的梯度。但為了計算能量及其質量的存在，我們顯然不能透過選擇另一個零電勢點來修改所有電荷的能量。零電勢點必須選擇得當，以便在不費力的情況下將電荷放置在那裡。這就是為什麼當我們計算電荷系統的靜電能量時，我們假設它們放置在真空中，並在無窮遠處定義零電勢。電荷產生的力在無窮遠處趨於零。如果我們離它們很遠，就不會有任何力量與它們的電場力作鬥爭。

當偶極矩由等量異號電荷的分離產生時，例如當為電容器充電時，我們可以推理，就像電荷密度最初在任何地方都為零一樣。因此，任何地方都沒有電場力。因此，任何點都可以選擇作為零電勢點。