在沒有電荷和電流的情況下,麥克斯韋方程組是




我們可以推匯出

或者  (本節末尾給出了
(本節末尾給出了 、
、 、
、 和
和  的證明)
的證明)

並且 
所以

其中 
 是波動方程。它的解是速度為
是波動方程。它的解是速度為  的光傳播的波,或者這些波的疊加。
的光傳播的波,或者這些波的疊加。
在空間中傳播的波是一個函式  的 4 個變數,x,y,z 和 t,3 個空間座標和一個時間座標。
的 4 個變數,x,y,z 和 t,3 個空間座標和一個時間座標。  是點
是點  的場。
的場。
要理解平面波,我們可以想象一個千層酥,它的每一層都可以相互滑動。然後,波可以在垂直於這些層的方向上傳播。如果一個移動的層帶著它相鄰的兩層,並且也被它們帶著,那麼千層酥一側的運動可以傳播到另一側。這種傳播運動就是平面波。


如果傳播方向是 x 軸,那麼這些層就是垂直平面,一個點的運動不依賴於它在層上的位置,只依賴於它的 x 橫座標。因此,平面波可以用一個函式  來表示,該函式只依賴於一個空間座標 x 和時間 t。它是一個一維波,因為它只依賴於一個空間座標。
來表示,該函式只依賴於一個空間座標 x 和時間 t。它是一個一維波,因為它只依賴於一個空間座標。
此外,如果這些層總是沿著同一個垂直方向移動,那麼它們的運動可以用一個數字來衡量,即它們在垂直方向上的運動。然後,平面波可以用一個函式  來表示,該函式的值是一個實數。如果運動更復雜,
來表示,該函式的值是一個實數。如果運動更復雜, 將是一個向量。
將是一個向量。
設  是一個實數的單變數實函式。
是一個實數的單變數實函式。  是一個實數,它只依賴於實數
是一個實數,它只依賴於實數  。
。
 可以表示平面中任何永遠不返回的曲線,從左到右無限延伸。這樣,對於每個
可以表示平面中任何永遠不返回的曲線,從左到右無限延伸。這樣,對於每個  ,線上都有一個座標為
,線上都有一個座標為  的唯一點。該點到水平軸的距離為
的唯一點。該點到水平軸的距離為  。
。
令  為兩個實數變數的實函式,定義為
為兩個實數變數的實函式,定義為

 代表一個平面波,以速度
代表一個平面波,以速度  無失真地傳播。
無失真地傳播。  的符號決定了傳播方向。 千層酥被波的傳播所變形,但
的符號決定了傳播方向。 千層酥被波的傳播所變形,但  形狀的變形不會改變。 它在整個旅程中保持不變。 因此,這種波可以將資訊從一個點傳輸到另一個點,無論距離多遠。
形狀的變形不會改變。 它在整個旅程中保持不變。 因此,這種波可以將資訊從一個點傳輸到另一個點,無論距離多遠。  是訊號傳播速度。
是訊號傳播速度。
電磁波是電場力  和磁場力
和磁場力  的波,以光速
的波,以光速  傳播。
傳播。
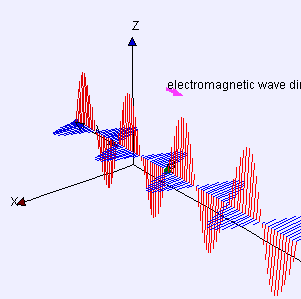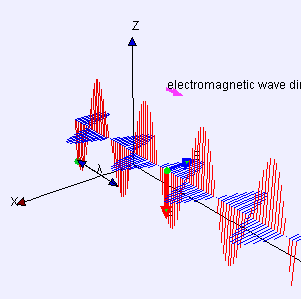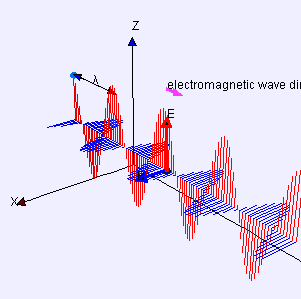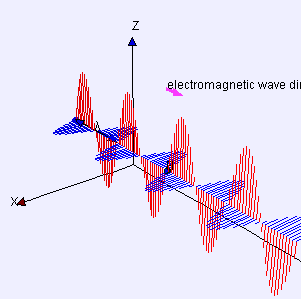
波  是波動方程
是波動方程  的解。
的解。
證明
由於  不依賴於 y 或 z,
不依賴於 y 或 z,

所以

現在


我們可以用相同的方式證明

所以  對所有 x 和所有 t 成立。
對所有 x 和所有 t 成立。
機械波是透過使質量運動來傳播的波。


麥克斯韋認為電磁波類似於在物質介質中傳播的機械波,他稱之為以太,它應該充滿整個宇宙,因為光無處不在,因為像聲波這樣的機械波不能在真空中傳播。
當波是機械波時,它的物質載體不會傳播。運動中的質量圍繞平衡位置振盪。在均勻和各向同性的介質中,波傳播的速度在所有方向上都是相同的。它是波相對於其物質載體的速度,當我們相對於該載體靜止時,我們測量的速度。如果我們相對於物質載體運動,則波的速度在所有方向上並不相同。
如果光在以太中傳播,我們必須觀察到它對方向的依賴性,因為我們不能總是相對於以太靜止。我們試圖觀察它,但從未成功。
相對論假設光速對所有觀察者來說都是相同的,無論他們的運動如何。從經典的觀點來看,這是荒謬的,因為相對運動中的觀察者測量的速度總是不一樣的。愛因斯坦證明,只要我們承認事件的同時性取決於觀察者的運動,就不會有任何矛盾。根據愛因斯坦的說法,時間不是絕對的,因為事件的同時性不是絕對的,而是相對於觀察者而言的。
如果光在以太中傳播,那麼對它速度的測量將取決於觀察者相對於以太的運動。所以相對論規定以太不存在。光是一種沒有物質載體的波。
電磁波是在真空中傳播的電磁力波。它們不是機械波,因為它們可以在沒有使質量運動的情況下傳播。
一個波  是單色的,頻率為
是單色的,頻率為  當且僅當對所有
當且僅當對所有  和所有
和所有  ,
,
 是角頻率,或稱為脈動。
是角頻率,或稱為脈動。
單色聲波是純淨的聲音。它的頻率越高,音調就越高。

單色光波是一種純色,即彩虹中的顏色,但非常明亮,就好像我們在夜空中看到了彩虹。低頻光為紅色。如果我們提高頻率,我們會到達紫色,這是最高的頻率,依次經過橙色、黃色、綠色和藍色。在紫色之外,我們發現紫外線、X 射線和  射線。在紅色之下,我們發現紅外線、微波和無線電波,它們的頻率可以低至我們想要的任何程度。
射線。在紅色之下,我們發現紅外線、微波和無線電波,它們的頻率可以低至我們想要的任何程度。

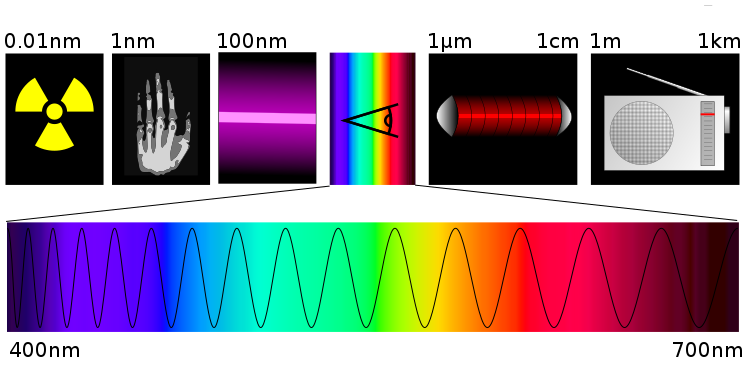
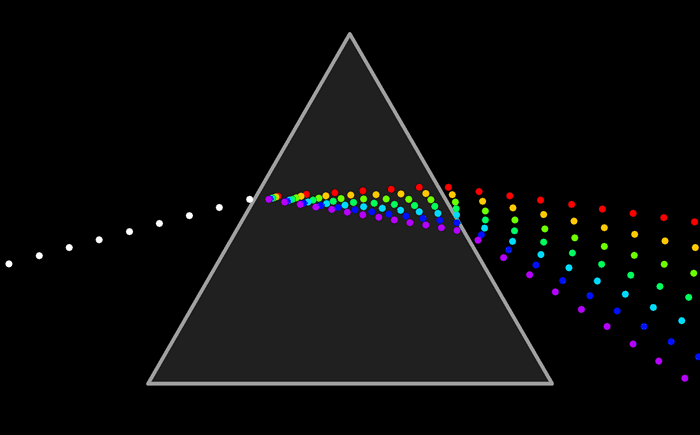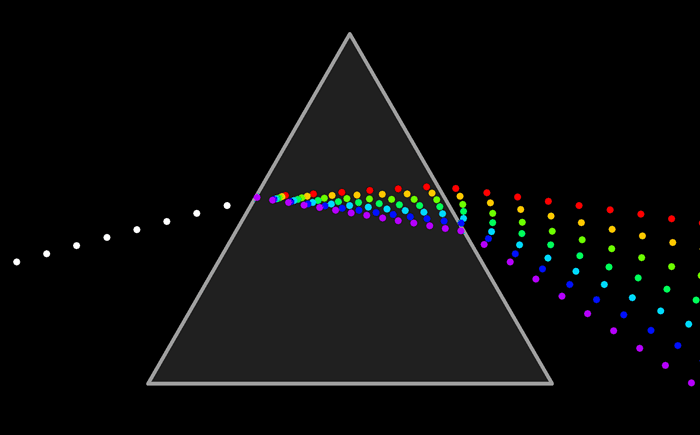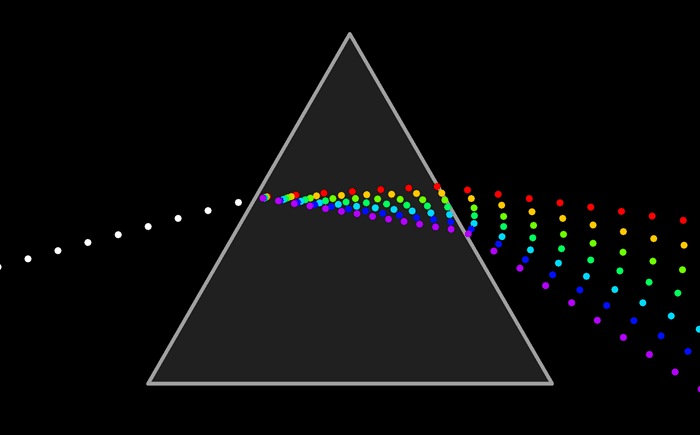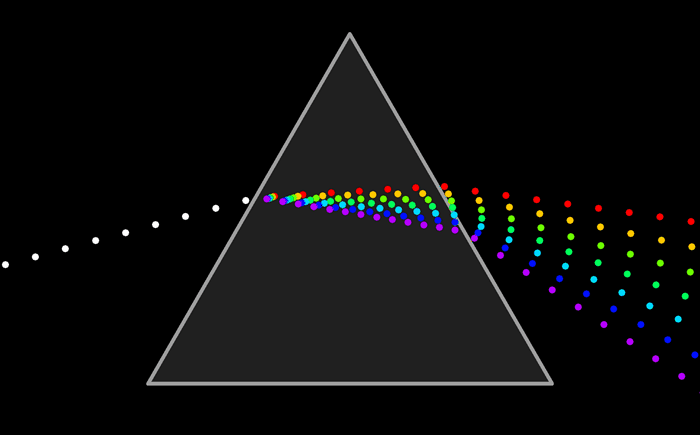
白光是由多種單色光疊加而成的。彩虹和稜鏡將白光的成分分開,從而揭示了它的光譜,即它的單色光成分。

一個脈動為  ,以速度
,以速度  傳播的單色平面波可以用函式
傳播的單色平面波可以用函式  表示,其中
表示,其中

其中  為常數,
為常數, ,
, 是波長。
是波長。
對  ,
, ,
, ,
, 和
和  的定義導致
的定義導致

如果  和
和  是波動方程
是波動方程  的兩個波動解,那麼
的兩個波動解,那麼  也是波動方程的波動解。
也是波動方程的波動解。
證明:和的導數是導數的和,所以  並且
並且  .
.
光子是光粒子。電磁波代表它們的運動。光子不會碰撞。一個被照亮的物體可以發射光,而不會受到照亮它的光線的阻礙,因為一個方向的光線不會受到另一個方向的光線的阻礙。光子可以相互穿過,而不必相互認識,就好像每個光子都可以穿過另一個光子一樣。波的疊加解釋了這種光子的相互漠不關心。兩個沿相反方向傳播的波在相遇點疊加,這種疊加不會影響它們的傳播。

波的疊加是一個非常普遍的原理,它可以解釋大多數現象,特別是白光的分解,因為它是由單色波的疊加構成的。
一個波  是靜止的當且僅當對於所有
是靜止的當且僅當對於所有  和所有
和所有  ,
,
這種波不會傳播。由  定義的形狀在原地振動,但不會移動。
定義的形狀在原地振動,但不會移動。
繃緊在兩端的一根弦的振動和鼓面的振動都是駐聲波。封閉在空腔中的空氣的振動,比如吉他內部的空氣,也是駐聲波。


設  和
和  是兩個相同的單色平面波,只是它們沿相反方向傳播。
是兩個相同的單色平面波,只是它們沿相反方向傳播。


 是一個駐波。
是一個駐波。
證明: 。所以
。所以 

如果光被困在兩塊平行鏡面之間,這兩塊鏡面都垂直於光傳播方向,光就會在兩塊鏡面上反射,因此同時以兩個相反的方向傳播。因此會產生駐波。困在雷射器內兩塊鏡面之間的光就是一個駐波。

聲波是壓力波。所有物體,無論是固體、液體還是氣體,都能振動。當它們振動時,就會導致相鄰物體振動。這種振動就是聲音。當聲音透過空氣傳播到耳朵時,它會使耳膜振動,耳膜就像一個非常小的鼓面。這種振動會被神經元轉化為電訊號,並傳播到大腦。
聲音也是密度波,因為物體的壓力取決於它們的密度。
聲音也是速度波,因為在沒有運動的情況下,物體的密度是恆定的。
回聲是聲音在懸崖或牆壁上反射,就像光線被鏡子反射一樣。
軟的牆壁不會反射聲音。牆壁越硬,它反射聲音的能力就越強。聲音的回聲就是它的反射,它在堅硬的牆壁上反彈。
非常硬的牆壁不會振動,或者幾乎不會振動。它的速度場為零。與之接觸的空氣也是如此。
水面的波浪會反射,因為它必須保持水平,垂直於反射它的牆壁。因此它的斜率為零。

如果一面鏡子是金屬的,那麼平行於其表面的電場為零,或者幾乎為零,因為電荷是可移動的,它們在不斷地移動以抵消使它們移動的電力。金屬鏡對光的行為就像硬的牆壁對聲波一樣,因為它抵消了平行於其表面的電場。
考慮一個平面波  ,它以不變形的形狀向右(x 遞增)傳播,它在位於
,它以不變形的形狀向右(x 遞增)傳播,它在位於  的點發出,該點朝向位於
的點發出,該點朝向位於  的反射壁傳播。
的反射壁傳播。  由它在
由它在  處的運動決定,它可以是波的發射源。
處的運動決定,它可以是波的發射源。
 因為
因為 
我們尋找波動方程的一個解  ,使得對於所有的 t,
,使得對於所有的 t, ,因為場必須在反射壁上抵消。
,因為場必須在反射壁上抵消。

根據  的定義,對於所有
的定義,對於所有  ,
, 。
。
 是兩個相互對稱的波的疊加。一個波是另一個波相對於反射壁的對稱反射,且方向相反。這兩個波,
是兩個相互對稱的波的疊加。一個波是另一個波相對於反射壁的對稱反射,且方向相反。這兩個波, 和
和  ,沿相反方向傳播。波
,沿相反方向傳播。波  可以由一個位於
可以由一個位於  的點發出,該點的運動方向與初始發射器的運動方向相反。
的點發出,該點的運動方向與初始發射器的運動方向相反。

一切現象都表明,反射壁產生了一個由一個與發射初始波的物體完全對稱的物體發出的波。這就是映象效應。我們在鏡子中看到的是,鏡子前方的物體就好像出現在鏡子後面一樣。


因此,電磁學解釋了為什麼金屬表面總是閃亮且具有反射性。

粗糙表面也會反射光,除非它們是黑色的且完全吸收光。但它們沒有鏡子的效果。

為了形成影像,影像平面上每個點只需要接收來自物體上單個點的發出的光即可。照亮影像中一個點的光源越寬,影像越模糊。
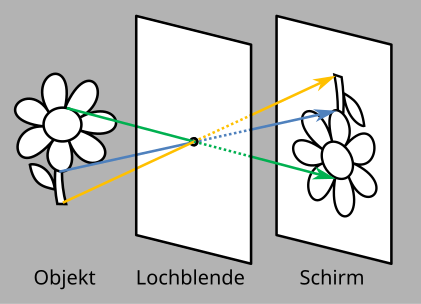
如果讓光穿過百葉窗上的一個小孔,我們可以在黑暗房間的白牆上看到一個影像。因此,我們可以看到陽光照射的對面立面在牆上或白布上形成一個倒置的投影。如果孔非常小,牆上的每個點都只接收來自立面上的單個點的光。如果孔很大,影像就會模糊。
兩種透明材料之間的彎曲介面具有使透過它的光會聚或發散的特性。


影像在眼睛後面形成,呈倒立狀態,因為來自物體上一個點的光會聚在眼睛後面的一個點上。

我們用麥克斯韋方程來解釋光在透明材料中的傳播。因此,影像的形成也是麥克斯韋方程的結果。
光的折射解釋了為什麼一根棍子在水面上看起來斷裂,以及為什麼透鏡可以使光波會聚或發散。
折射是由光在兩種透明材料之間傳播速度的差異造成的。光在透明材料中的傳播速度總是比在真空中慢,真空中光速為 300,000 公里/秒。在空氣中,這種減速非常小,但在水中,光速降至約 215,000 公里/秒,在鑽石中,光速降至 125,000 公里/秒。
當光的傳播方向垂直於兩種材料之間的介面時,光的傳播方向不會改變。

但光的傳播方向偏轉的程度與其初始傳播方向偏離介面法線方向的程度成正比。


如果我們把頭浸在水裡,看著水池的邊緣,看起來生物比實際距離更遠。

反之,如果我們在空氣中,看著水下的生物,看起來它們比實際距離更近。這就是為什麼棍子看起來在水面處斷裂的原因。

在這張照片中,我們可以看到刷子在水面上看起來斷裂,而且看起來被玻璃的彎曲表面放大,就好像這個表面是一塊放大鏡一樣。
光總是遵循費馬原理:光線所走的路徑在所有可能的路徑中總是最短的。
一名救生員在海灘上。如果她需要救的人在她面前,她會選擇最短的路徑,也就是一條與海灘線垂直的直線。如果需要救援的人不在她面前,她就不能走直線,因為她在海灘上奔跑的速度比在水裡游泳的速度快。因此,她必須選擇一條折線作為她的路線,先在海灘上奔跑,幾乎跑到需要救援的人的面前,然後才開始游泳。光在從空氣進入水時也是這樣做的。
智慧在於從眾多可能性中選擇最佳的,或者至少選擇一個令人滿意的。光總是選擇最短的路徑,因為它沒有時間浪費。
光在水和其他透明材料中減速可以用麥克斯韋和洛倫茲方程來解釋。當光穿過一種材料時,它的電荷開始移動,並本身成為發光源。入射波與感應波的疊加是導致結果波速降低以及光折射的原因。
疊加原理最令人驚奇的結果之一是光加光可以等於黑暗。
我們觀察到的光的能量與 成正比,即它傳播的電場標量的平方。如果兩個光源產生相等且相反的電場,它們的疊加將產生零場,沒有能量,因此沒有光,也就是黑暗。
成正比,即它傳播的電場標量的平方。如果兩個光源產生相等且相反的電場,它們的疊加將產生零場,沒有能量,因此沒有光,也就是黑暗。
在楊氏雙縫實驗中,兩個狹縫允許光透過。如果我們在接收光的螢幕上觀察光,我們會看到明暗條紋交替出現,但黑暗部分像明亮部分一樣被兩個狹縫照亮。

楊在1803年認識到,相反方向的波會相互抵消,而當它們具有相同方向時,它們會疊加。

太陽鏡有時會使用偏振鏡片。

當光具有垂直於其傳播方向的方向時,它就被線偏振。偏振器是一種濾光器,它會阻止一個方向上偏振的光透過,而允許垂直方向上偏振的光透過。

圓偏振是兩個線偏振波的疊加。
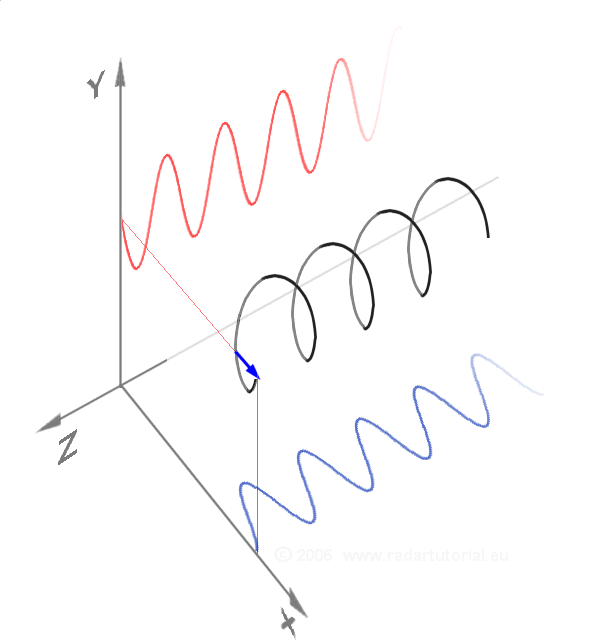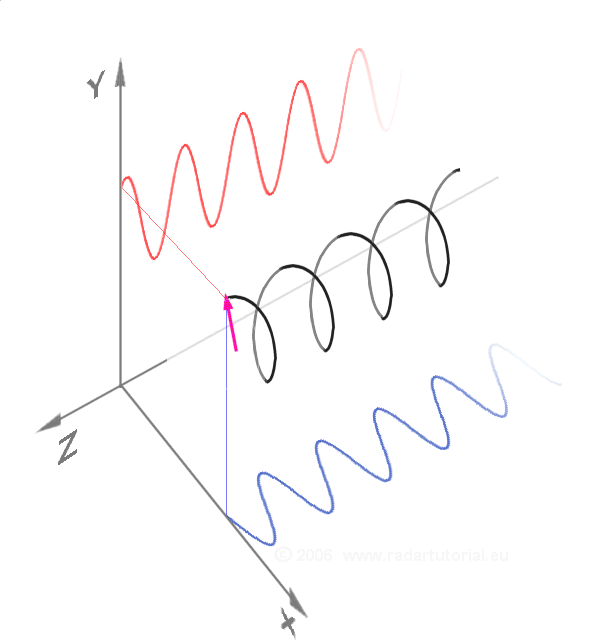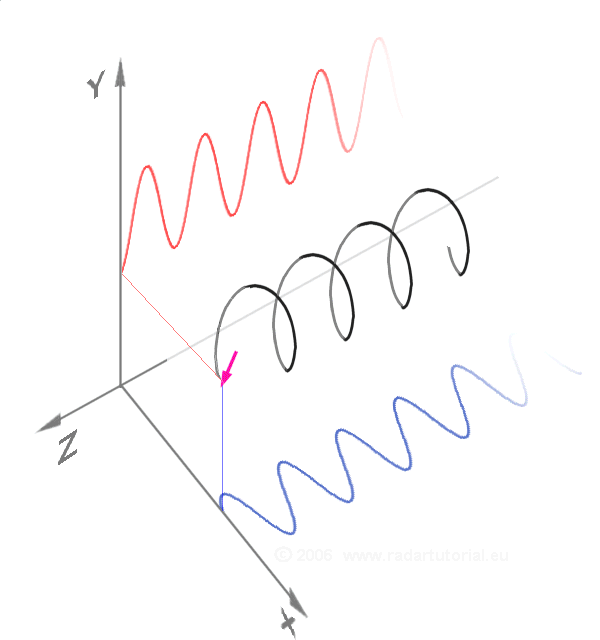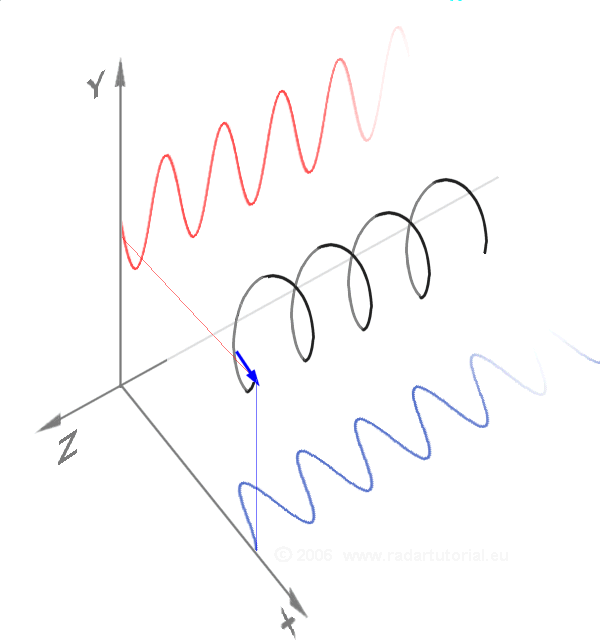
當光被圓偏振時,它會在其傳播方向周圍旋轉。對於量子物理學,光的偏振是光子的自旋。光子具有自旋意味著它們具有旋轉慣性,就像旋轉的陀螺一樣。旋轉慣性是使物體保持相同的軸和相同的旋轉速度的原因。它使移動的腳踏車保持平衡。靜止的腳踏車沒有這種平衡,因為它們的輪子不轉。
來自太陽或來自白熾發光材料的光是不偏振的。但是天空中的光是被偏振的。透過反射鏡、水或玻璃反射獲得的光也可以被偏振。
要檢視光是否被偏振,只需透過一個偏振玻璃觀察它,該玻璃圍繞垂直於其表面的軸旋轉。

這兩張照片是用偏振濾光器拍攝的,該濾光器在左右影像之間旋轉了 90°。
當我們對材料施加應力時,它通常表現得像偏振器一樣。這種偏振效應揭示了應力。

如果我們將晶體放在兩個交叉的偏振器之間,然後旋轉它們,我們可以獲得非常美麗的效果,因為雙折射晶體表現得像偏振器一樣。

麥克斯韋方程表明,線偏振光的偏振方向是電場 的方向。
的方向。
 和
和 始終垂直於電磁波的傳播方向。
始終垂直於電磁波的傳播方向。
平面波的證明:關於 y 和 z 的偏導數為零,因為場既不依賴於 y 也不依賴於 z。根據麥克斯韋第四個方程,電場 傳播方向上的
傳播方向上的 分量使得
分量使得 。由於
。由於 不能隨時間變化,因此它不能傳播波。因此,對於傳播波,它為零。相同的論點適用於
不能隨時間變化,因此它不能傳播波。因此,對於傳播波,它為零。相同的論點適用於 ,來自麥克斯韋第三個方程。
,來自麥克斯韋第三個方程。
麥克斯韋和洛倫茲方程預測了光的產生和所有性質:光的傳播、顏色、駐波、反射、成像原理、折射、干涉和偏振。 它們使得我們可以研究物質的大多數特性(除核起源的放射性和重力外)及其與光的相互作用。
電磁場具有自主存在。 一旦加速的電荷產生光,光就會自行傳播,產生它的電荷就無法再阻止它。
上帝在賦予麥克斯韋方程(或庫侖定律和時空的相對論幾何)的同時,也賦予了光存在的規律,使我們能夠看到光,並藉此看到世界。 上帝說:“要有光”,從而賦予了電磁定律,即麥克斯韋和洛倫茲方程。
標量場的梯度、向量場的散度和旋度是物理學家在大多數計算中使用的三個基本運算元,特別是在電動力學和流體力學中。 所有三個都可以用 nabla  運算元表示
運算元表示





 因此可以寫成
因此可以寫成

證明 ∇×(∇×**A**)=∇(∇·**A**)-∇2**A**
(∇×(∇×**A**))x=∂/∂y(∂Ay/∂x-∂Ax/∂y)-∂/∂z(∂Ax/∂z-∂Az/∂x)
=∂/∂x(∂Ay/∂y+∂Az/∂z)-(∂2/∂y2+∂2/∂z2)Ax
=∂/∂x(∂Ax/∂x+∂Ay/∂y+∂Az/∂z)-(∂2/∂x2+∂2/∂y2+∂2/∂z2)Ax
其他兩個分量的計算方法類似。



















































































































