電動力學/電場

電場

電場是由帶電物體產生的物理場，它影響附近帶電物體在電場中的行為。電場無限地延伸到整個空間，描述了電相互作用。

使用庫侖定律，我們可以將點電荷放置在相對於其他電荷的任何位置，並確定該點電荷上的力。電場是一個向量場，其中空間中的每個點都被分配一個力向量，具體取決於場對該點電荷的影響。

數學表示

有多種數學方法可以表示電場。第一種方法將電場視為三維向量場。該向量場在空間和時間的每個點都有一個定義的值，因此通常被認為是空間和時間座標的函式。因此，它通常寫成 E(x, y, z, t)。如果該場是靜電的，則通常會從描述中省略t項。此外，如果我們使用的是向量符號而不是笛卡爾座標，我們可以將該場寫成

$\mathbf {E} (\mathbf {r} )=\mathbf {E} (x,y,z)$

電場定義為點電荷q上力的極限，除以該點電荷的值，當電荷趨於零時。數學上

$\mathbf {E} (\mathbf {r} )=\lim _{q\to 0}{\frac {\mathbf {F} _{q}}{q}}$

我們取極限的原因非常重要：如果我們在系統中新增一個大於 0 的電荷，那麼測試點電荷將影響系統並改變它。我們取極限並將測試電荷減小到零，以便它不會影響系統的其餘部分。

使用我們的電荷密度函式 ρ，我們可以計算一個具有均勻電荷的大物體（如帶電介質）對點電荷q施加的力。為此，我們將我們針對n個電荷的庫侖定律擴充套件到具有連續電荷分佈的類似定律

$\mathbf {E} =\int {\frac {\rho (\mathbf {r} ')(\mathbf {r} -\mathbf {r} ')}{4\pi \epsilon |\mathbf {r} -\mathbf {r} '|^{3}}}dV$

在場的每個點r處，都有一個由庫侖定律給出的相關力。

電場（由點電荷引起）

另一種考慮E場的方法，而不是抽象的數學方程，是考慮單個點電荷。我們將點電荷放置在場的不同位置，並“測量”（使用庫侖定律）場對點電荷的影響。我們可以使用這些測量結果來繪製等勢線，即點電荷上的力相等的線。

在進行這些測量時，我們使用無限小的點電荷，因為在系統中新增非無限小的電荷會影響場，並對場中的其他粒子施加力。

靜電場

如果電場 (E) 不為零，並且在時間上是恆定的，則該場被稱為靜電場。例如，如果以下關係成立，則該場為靜電場

$\mathbf {E} (x,y,z,t_{1})=\mathbf {E} (x,y,z,t_{0})$

如果此等式對x、y、z、t₁ 和 t₀ 的所有值都成立，則該場為靜電場。如果此等式不成立，則該場隨時間變化，稱為電動力學。

符號

我們知道電場是位置（以及可能的時間）的函式，因此在大多數應用中通常會省略所有引數。我們將在本書的其餘部分使用粗體字母 E 表示電場。這是一種非常標準的電場符號，許多關於該主題的書籍會簡單地將其稱為 E 場，或簡稱“E 場”。我們也將在本書中遵循此慣例。

電場線

為了幫助我們視覺化電場，我們使用一種稱為電場線的圖形符號。電場線是連線異號電荷的線。根據一般慣例，我們說電場線從正電荷發出，進入負電荷，如下所示

在繪製電場線時，我們有一些通用規則

1. 電場線不能交叉或重疊。
2. 電場線必須從正電荷開始，在負電荷結束。
3. 電場線應該均勻彎曲，並且不應有任何角度。

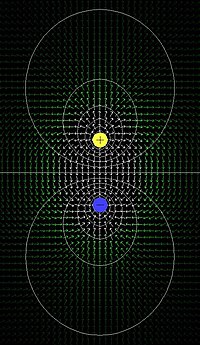
如果我們繪製所有電場線，我們將開始看到我們的電場。

勢函式

對於靜電場，旋度為零（可以驗證）。這意味著力是保守的；存在一個勢能函式，使得任何兩點的勢能差等於將電荷從一個點移動到另一個點的任何路徑所需的功。

與電場一樣，如果我們定義勢能為場的屬性，將是可取的。這將不再是勢能；顯然，電荷越大，移動它所需的功就越多。但是，我們可以定義一個勢，它等於單位電荷的功，是場的固有屬性。勢的單位是焦耳每庫侖。這在實際中使用如此普遍，以至於它被賦予了自己的名稱，即伏特。

我們將φ(r) 設定為電場內位置的勢函式。我們可以用 E 場來定義勢函式

[勢函式]

$\phi (\mathbf {r} )=\int _{\mathbf {r} \to \infty }\mathbf {E} \cdot dl$

或者，如果我們對兩邊求導，我們得到

$\nabla \phi (\mathbf {r} )=-\mathbf {E}$

通常，找到勢函式比直接找到 E 場更容易。

使用高斯定律，我們可以將場的勢函式與場中一點的電荷密度聯絡起來，如下所示

$\nabla ^{2}\phi =-\rho /\epsilon$

當我們討論電能時，我們將更詳細地討論勢函式。